2026年一本密卷高考数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年一本密卷高考数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
8. (2025·安徽省安庆市三模)如图,棱长为 2 的正方体 $ABCD - A_1B_1C_1D_1$ 中,$P$,$Q$ 分别是棱 $CC_1$,棱 $BC$ 的中点,动点 $M$ 满足 $\overrightarrow{DM} = \lambda\overrightarrow{DA} + \mu\overrightarrow{DD_1}$,其中 $\lambda,\mu\in\mathbf{R}$,则下列结论正确的是(
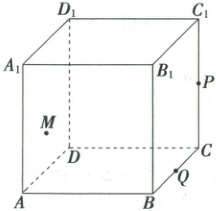
A.若 $\lambda + \mu = 1$,则 $CM\perp DB_1$
B.若 $\lambda = \mu$,则三棱锥 $B_1 - AMC$ 的体积为定值
C.若 $\mu = \frac{1}{2},0\leqslant\lambda\leqslant 1$,则直线 $PM$ 与直线 $BC$ 所成角的最小值为 $60^{\circ}$
D.若动点 $M$ 在三棱锥 $C - DPQ$ 外接球的表面上,则点 $M$ 的轨迹长度为 $\sqrt{2}\pi$
ABD
)
A.若 $\lambda + \mu = 1$,则 $CM\perp DB_1$
B.若 $\lambda = \mu$,则三棱锥 $B_1 - AMC$ 的体积为定值
C.若 $\mu = \frac{1}{2},0\leqslant\lambda\leqslant 1$,则直线 $PM$ 与直线 $BC$ 所成角的最小值为 $60^{\circ}$
D.若动点 $M$ 在三棱锥 $C - DPQ$ 外接球的表面上,则点 $M$ 的轨迹长度为 $\sqrt{2}\pi$
答案:
8.ABD 以$D$为坐标原点,$DA,DC,DD_{1}$所在直线为坐标轴建立如图所示的空间直角坐标系,则$D(0,0,0)$,

$A(2,0,0)$,$D_{1}(0,0,2)$,$B_{1}(2,2,2)$,$C(0,2,0)$,所以$\overrightarrow{DA} = (2,0,0)$,$\overrightarrow{DD_{1}} = (0,0,2)$,所以$\overrightarrow{DM} = \lambda\overrightarrow{DA} + \mu\overrightarrow{DD_{1}} = \lambda(2,0,0) + \mu(0,0,2) =(2\lambda,0,2\mu)$,设$M(2\lambda,0,2\mu)$,所以$\overrightarrow{CM} = (2\lambda,-2,2\mu)$,又$\overrightarrow{DB_{1}} = (2,2,2)$,所以$\overrightarrow{CM} · \overrightarrow{DB_{1}} = 2\lambda × 2 + (-2) × 2 + 2\mu × 2 =4(\lambda + \mu) - 4 = 0$,所以$\overrightarrow{CM} \perp \overrightarrow{DB_{1}}$,故A正确;因为$\lambda = \mu$,$\overrightarrow{DM} = \lambda\overrightarrow{DA} + \mu\overrightarrow{DD_{1}}$,所以点$M$在直线$DA_{1}$上,又因为$A_{1}B_{1}// AB// DC$,$A_{1}B_{1} = AB = DC$,所以四边形$A_{1}DCB_{1}$是平行四边形,又$A_{1}D\subset$平面$B_{1}AC$,$B_{1}C\subset$平面$B_{1}AC$,所以$A_{1}D//$平面$B_{1}AC$,又$A_{1}D \subset$平面$ADD_{1}A_{1}$,$CC_{1}\subset$平面$ADD_{1}A_{1}$,平面$ADD_{1}A_{1}//$平面$B_{1}AC$,所以$M$到平面$B_{1}AC$的距离为定值,又$\triangle B_{1}AC$的面积为定值,所以三棱锥$B_{1} - AMC$的体积为定值,故B正确;点$P$为$CC_{1}$的中点,坐标为$(0,2,1)$,点$M$的坐标为$(2\lambda,0,1)$,向量$\overrightarrow{PM} = (2\lambda,-2,0)$,向量$\overrightarrow{BC} = (-2,0,0)$,设直线$\overrightarrow{PM}$与直线$BC$所成的角为$\theta$,$\cos\theta = \frac{|\overrightarrow{PM} · \overrightarrow{BC}|}{|\overrightarrow{PM}|·|\overrightarrow{BC}|} =\frac{|-4\lambda|}{\sqrt{4\lambda^{2} + 4} × 2} = \frac{|\lambda|}{\sqrt{\lambda^{2} + 1}}$,又因为$0 \leqslant \lambda \leqslant1$,当$\lambda = 1$时,$(\cos\theta)_{\max} = \frac{1}{\sqrt{2}}$,即直线$PM$与直线$BC$所成角的最小值为$45^{\circ}$,故C错误;因为三棱锥$C - DPQ$即为三棱锥$P - CDQ$,又底面$\triangle CDQ$是直角三角形,过$DQ$的中点$N$作$ON \perp$平面$CDQ$,$O$是三棱锥$C - DPQ$外接球的球心,因为$PC \perp$平面$CDQ$,所以$ON = \frac{1}{2}PC = \frac{1}{2}$,又$DQ = \sqrt{2^{2} + 1^{2}} = \sqrt{5}$,所以三棱锥$C - DPQ$外接球的半径$r = \sqrt{(\frac{\sqrt{5}}{2})^{2} + (\frac{1}{2})^{2}} = \frac{\sqrt{6}}{2}$,因为点$M$在平面$ADD_{1}A_{1}$内,又在三棱锥$C - DPQ$外接球的表面上,所以$M$的轨迹是平面$ADD_{1}A_{1}$截三棱锥$C - DPQ$外接球的截面圆,又易得$O$到平面$ADD_{1}A_{1}$的距离为1,所以截面圆的半径为$\sqrt{(\frac{\sqrt{6}}{2})^{2} - 1^{2}} = \frac{\sqrt{2}}{2}$,则$M$的轨迹的周长为$2\pi × \frac{\sqrt{2}}{2} = \sqrt{2}\pi$,故D正确.故选ABD.
8.ABD 以$D$为坐标原点,$DA,DC,DD_{1}$所在直线为坐标轴建立如图所示的空间直角坐标系,则$D(0,0,0)$,

$A(2,0,0)$,$D_{1}(0,0,2)$,$B_{1}(2,2,2)$,$C(0,2,0)$,所以$\overrightarrow{DA} = (2,0,0)$,$\overrightarrow{DD_{1}} = (0,0,2)$,所以$\overrightarrow{DM} = \lambda\overrightarrow{DA} + \mu\overrightarrow{DD_{1}} = \lambda(2,0,0) + \mu(0,0,2) =(2\lambda,0,2\mu)$,设$M(2\lambda,0,2\mu)$,所以$\overrightarrow{CM} = (2\lambda,-2,2\mu)$,又$\overrightarrow{DB_{1}} = (2,2,2)$,所以$\overrightarrow{CM} · \overrightarrow{DB_{1}} = 2\lambda × 2 + (-2) × 2 + 2\mu × 2 =4(\lambda + \mu) - 4 = 0$,所以$\overrightarrow{CM} \perp \overrightarrow{DB_{1}}$,故A正确;因为$\lambda = \mu$,$\overrightarrow{DM} = \lambda\overrightarrow{DA} + \mu\overrightarrow{DD_{1}}$,所以点$M$在直线$DA_{1}$上,又因为$A_{1}B_{1}// AB// DC$,$A_{1}B_{1} = AB = DC$,所以四边形$A_{1}DCB_{1}$是平行四边形,又$A_{1}D\subset$平面$B_{1}AC$,$B_{1}C\subset$平面$B_{1}AC$,所以$A_{1}D//$平面$B_{1}AC$,又$A_{1}D \subset$平面$ADD_{1}A_{1}$,$CC_{1}\subset$平面$ADD_{1}A_{1}$,平面$ADD_{1}A_{1}//$平面$B_{1}AC$,所以$M$到平面$B_{1}AC$的距离为定值,又$\triangle B_{1}AC$的面积为定值,所以三棱锥$B_{1} - AMC$的体积为定值,故B正确;点$P$为$CC_{1}$的中点,坐标为$(0,2,1)$,点$M$的坐标为$(2\lambda,0,1)$,向量$\overrightarrow{PM} = (2\lambda,-2,0)$,向量$\overrightarrow{BC} = (-2,0,0)$,设直线$\overrightarrow{PM}$与直线$BC$所成的角为$\theta$,$\cos\theta = \frac{|\overrightarrow{PM} · \overrightarrow{BC}|}{|\overrightarrow{PM}|·|\overrightarrow{BC}|} =\frac{|-4\lambda|}{\sqrt{4\lambda^{2} + 4} × 2} = \frac{|\lambda|}{\sqrt{\lambda^{2} + 1}}$,又因为$0 \leqslant \lambda \leqslant1$,当$\lambda = 1$时,$(\cos\theta)_{\max} = \frac{1}{\sqrt{2}}$,即直线$PM$与直线$BC$所成角的最小值为$45^{\circ}$,故C错误;因为三棱锥$C - DPQ$即为三棱锥$P - CDQ$,又底面$\triangle CDQ$是直角三角形,过$DQ$的中点$N$作$ON \perp$平面$CDQ$,$O$是三棱锥$C - DPQ$外接球的球心,因为$PC \perp$平面$CDQ$,所以$ON = \frac{1}{2}PC = \frac{1}{2}$,又$DQ = \sqrt{2^{2} + 1^{2}} = \sqrt{5}$,所以三棱锥$C - DPQ$外接球的半径$r = \sqrt{(\frac{\sqrt{5}}{2})^{2} + (\frac{1}{2})^{2}} = \frac{\sqrt{6}}{2}$,因为点$M$在平面$ADD_{1}A_{1}$内,又在三棱锥$C - DPQ$外接球的表面上,所以$M$的轨迹是平面$ADD_{1}A_{1}$截三棱锥$C - DPQ$外接球的截面圆,又易得$O$到平面$ADD_{1}A_{1}$的距离为1,所以截面圆的半径为$\sqrt{(\frac{\sqrt{6}}{2})^{2} - 1^{2}} = \frac{\sqrt{2}}{2}$,则$M$的轨迹的周长为$2\pi × \frac{\sqrt{2}}{2} = \sqrt{2}\pi$,故D正确.故选ABD.
9. (2025·江苏苏州质量检测)已知圆柱的上、下底面圆周在同一球面上,且球的表面积是圆柱的表面积的 2 倍,则球的体积与圆柱的体积的比值是
$\frac{5\sqrt{5}}{3}$
.
答案:
9.$\frac{5\sqrt{5}}{3}$ 设球的半径为$R$,圆柱底面的半径为$r$,圆柱的母线长为$l$,则球的表面积为$S_{1} = 4\pi R^{2}$,圆柱的表面积为$S_{2} = 2\pi r^{2} + 2\pi rl$,所以$\frac{S_{1}}{S_{2}} = \frac{4\pi R^{2}}{2\pi r^{2} + 2\pi rl} =2$,得$R^{2} = r^{2} + rl$ ①,又圆柱的上、下底面圆周在同一球面上,所以$(\frac{l}{2})^{2} + r^{2} = R^{2}$ ②,由①②解得$l = 4r$,$R = \sqrt{5}r$,所以球的体积为$V_{1} = \frac{4}{3}\pi R^{3} = \frac{20\sqrt{5}\pi r^{3}}{3}$,圆柱的体积为$V_{2} = \pi r^{2}l = 4\pi r^{3}$,$\frac{V_{1}}{V_{2}} =\frac{\frac{20\sqrt{5}\pi r^{3}}{3}}{4\pi r^{3}} = \frac{5\sqrt{5}}{3}$.
10. (2025·浙江宁波质量检测)已知四棱锥 $P - ABCD$ 的底面为边长为 2 的正方形,$PB = PC = BC$,$PA = PD = \sqrt{2}AB$,$M,N$ 分别为 $AB$ 和 $PC$ 的中点,则平面 $DMN$ 上任意一点到底面 $ABCD$ 中心距离的最小值为
$\frac{\sqrt{3}}{8}$
.
答案:
10.$\frac{\sqrt{3}}{8}$ $\because$四棱锥$P - ABCD$的底面为边长为2的正方形,连接$AC,BD$且相交于点$O$,则点$O$是底面$ABCD$中心,$PB = PC = BC = 2$,取$BC$的中点$F$,连接$PF$,则$PF \perp BC$,又$\because PA = PD = \sqrt{2}AB = 2\sqrt{2}$,$\therefore DC^{2} + CP^{2} = 2^{2} + 2^{2} = (2\sqrt{2})^{2} = DP^{2}$,$AB^{2} +BP^{2} = 2^{2} + 2^{2} = (2\sqrt{2})^{2} = AP^{2}$,$\therefore PC \perp DC$,$AB \perp PB$,又$PC \cap BC = P$,$AB// DC$,$\therefore CD \perp$面$PBC$,又$\because CD\subset$面$ABCD$,$\therefore$面$PBC\perp$面$ABCD$,又$\because PF\perp BC$,$BC$为面$PBC$与面$ABCD$的交线,$PF\subset$平面$PBC$,$\therefore PF\perp$面$ABCD$,又$OFC\subset$面$ABCD$,$CFC\subset$面$ABCD$,$\therefore PF\perp OF$,$PF\perp CF$.以$F$点为原点,以$FC,FO,FP$分别为$x$轴,$y$轴,$z$轴建立空间直角坐标系,则$O(0,1,0)$,$D(1,2,0)$,$M(-1,1,0)$,$N(\frac{1}{2},0,\frac{\sqrt{3}}{2})$,设平面$DMN$的法向量为$\mathbf{m} = (x,y,z)$,设$O$到平面$DMN$的距离为$d$,则$\begin{cases} \mathbf{m} · \overrightarrow{DM} = 0 \\\mathbf{m} · \overrightarrow{NM} = 0 \end{cases}$,$\begin{cases} (x,y,z) · (-2,-1,0) = 0 \\(x,y,z) · (-\frac{3}{2},1, - \sqrt{3}) = 0 \end{cases}$,$\begin{cases} 2x + y = 0 \\3x - 2y + \sqrt{3}z = 0 \end{cases}$,令$x = \1$,则$\mathbf{m} = (1,-2, - \frac{7\sqrt{3}}{3})$,代入距离公式得$d = \frac{|\mathbf{m} · \overrightarrow{OD}|}{|\mathbf{m}|} =\frac{|1 × 1 + (-2) × 1 + 0 × (-\frac{7\sqrt{3}}{3})|}{\sqrt{1^{2} + (-2)^{2} + (-\frac{7\sqrt{3}}{3})^{2}}} = \frac{\sqrt{3}}{8}$.

10.$\frac{\sqrt{3}}{8}$ $\because$四棱锥$P - ABCD$的底面为边长为2的正方形,连接$AC,BD$且相交于点$O$,则点$O$是底面$ABCD$中心,$PB = PC = BC = 2$,取$BC$的中点$F$,连接$PF$,则$PF \perp BC$,又$\because PA = PD = \sqrt{2}AB = 2\sqrt{2}$,$\therefore DC^{2} + CP^{2} = 2^{2} + 2^{2} = (2\sqrt{2})^{2} = DP^{2}$,$AB^{2} +BP^{2} = 2^{2} + 2^{2} = (2\sqrt{2})^{2} = AP^{2}$,$\therefore PC \perp DC$,$AB \perp PB$,又$PC \cap BC = P$,$AB// DC$,$\therefore CD \perp$面$PBC$,又$\because CD\subset$面$ABCD$,$\therefore$面$PBC\perp$面$ABCD$,又$\because PF\perp BC$,$BC$为面$PBC$与面$ABCD$的交线,$PF\subset$平面$PBC$,$\therefore PF\perp$面$ABCD$,又$OFC\subset$面$ABCD$,$CFC\subset$面$ABCD$,$\therefore PF\perp OF$,$PF\perp CF$.以$F$点为原点,以$FC,FO,FP$分别为$x$轴,$y$轴,$z$轴建立空间直角坐标系,则$O(0,1,0)$,$D(1,2,0)$,$M(-1,1,0)$,$N(\frac{1}{2},0,\frac{\sqrt{3}}{2})$,设平面$DMN$的法向量为$\mathbf{m} = (x,y,z)$,设$O$到平面$DMN$的距离为$d$,则$\begin{cases} \mathbf{m} · \overrightarrow{DM} = 0 \\\mathbf{m} · \overrightarrow{NM} = 0 \end{cases}$,$\begin{cases} (x,y,z) · (-2,-1,0) = 0 \\(x,y,z) · (-\frac{3}{2},1, - \sqrt{3}) = 0 \end{cases}$,$\begin{cases} 2x + y = 0 \\3x - 2y + \sqrt{3}z = 0 \end{cases}$,令$x = \1$,则$\mathbf{m} = (1,-2, - \frac{7\sqrt{3}}{3})$,代入距离公式得$d = \frac{|\mathbf{m} · \overrightarrow{OD}|}{|\mathbf{m}|} =\frac{|1 × 1 + (-2) × 1 + 0 × (-\frac{7\sqrt{3}}{3})|}{\sqrt{1^{2} + (-2)^{2} + (-\frac{7\sqrt{3}}{3})^{2}}} = \frac{\sqrt{3}}{8}$.

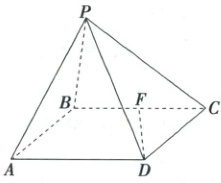
11. (13 分)(2025·湖南省永州市三模)如图,在四棱锥 $P - ABCD$ 中,底面 $ABCD$ 为菱形,$\angle BAD = \frac{\pi}{3}$,$\triangle PAB$ 是边长为 2 的等边三角形,$F$ 为 $BC$ 的中点.
(1)证明:$AB\perp PD$;
(2)若直线 $AP$ 与 $DF$ 的夹角的余弦值为 $\frac{\sqrt{3}}{6}$,求直线 $PC$ 与平面 $PAB$ 所成角的正弦值.
(1)证明:$AB\perp PD$;
(2)若直线 $AP$ 与 $DF$ 的夹角的余弦值为 $\frac{\sqrt{3}}{6}$,求直线 $PC$ 与平面 $PAB$ 所成角的正弦值.

答案:
11.解:
(1)证明:记AB的中点为O,连接PO,OD,BD,因为ABCD为菱形,$\angle BAD = \frac{\pi}{3},$所以$\triangle ABD$为正三角形,所以$OD \perp AB,$由$\triangle PAB$为正三角形可得$PO \perp AB,$因为OP,OD是平面POD内的两条相交直线,所以$AB \perp$平面POD,因为$PD\subset$平面POD,所以$AB \perp PD.$

(2)由
(1)知,$AB \perp OD,$过点O作$Oz\perp$平面ABCD,以OA,OD,Oz所在直线分别为x,y,z轴建立空间直角坐标系,因为$AB\perp$平面POD,所以点P在坐标平面yOz内,设$\angle POD = \alpha,$$PO = OD =\sqrt{3},$则$P(0,\sqrt{3}\cos\alpha,\sqrt{3}\sin\alpha),$A(1,0,0),$D(0,\sqrt{3},0),$B(-1,0,0),$C(-2,\sqrt{3},0),$$F( - \frac{3}{2},\frac{\sqrt{3}}{2},0),$所以$\overrightarrow{AP} = (-1,\sqrt{3}\cos\alpha,\sqrt{3}\sin\alpha),$$\overrightarrow{DF} =( - \frac{3}{2}, - \frac{\sqrt{3}}{2},0),$$\overrightarrow{AB} = (-2,0,0),$因为直线AP与DF的夹角的余弦值为$\frac{\sqrt{3}}{6},$所以$\frac{|\overrightarrow{AP} · \overrightarrow{DF}|}{|\overrightarrow{AP}||\overrightarrow{DF}|} = \frac{\sqrt{3}}{6},$$\frac{|\frac{3}{2} - \frac{3}{2}\cos\alpha|}{2\sqrt{3}} = \frac{\sqrt{3}}{6},$解得$\cos\alpha = \frac{1}{3},$因为$\alpha \in (0,\pi),$所以$\sin\alpha = \frac{2\sqrt{2}}{3},$得$P(0,\frac{\sqrt{3}}{3},\frac{2\sqrt{6}}{3}),$所以$\overrightarrow{AP} = (-1,\frac{\sqrt{3}}{3},\frac{2\sqrt{6}}{3}),$$\overrightarrow{PC} = (-2,\frac{2\sqrt{3}}{3}, - \frac{2\sqrt{6}}{3}),$设平面PAB的法向量为$\mathbf{n} = (x,y,z),$

则$\begin{cases} \overrightarrow{AP} · \mathbf{n} = - x + \frac{\sqrt{3}}{3}y + \frac{2\sqrt{6}}{3}z = 0 \\\overrightarrow{AB} · \mathbf{n} = -2x = 0 \end{cases},$令$x = 2\sqrt{2},$得$\mathbf{n} = (0,2\sqrt{2}, -1),$记直线PC与平面PAB所成角为$\theta,$则$\sin\theta =$|$\frac{\overrightarrow{PC} · \mathbf{n}}{|\overrightarrow{PC}||\mathbf{n}|}$|$ = \frac{|\frac{2\sqrt{6}}{3}|}{\sqrt{2^{2} × 3} × \sqrt{1 + 8 + 1}} = \frac{\sqrt{3}}{3}.$
11.解:
(1)证明:记AB的中点为O,连接PO,OD,BD,因为ABCD为菱形,$\angle BAD = \frac{\pi}{3},$所以$\triangle ABD$为正三角形,所以$OD \perp AB,$由$\triangle PAB$为正三角形可得$PO \perp AB,$因为OP,OD是平面POD内的两条相交直线,所以$AB \perp$平面POD,因为$PD\subset$平面POD,所以$AB \perp PD.$

(2)由
(1)知,$AB \perp OD,$过点O作$Oz\perp$平面ABCD,以OA,OD,Oz所在直线分别为x,y,z轴建立空间直角坐标系,因为$AB\perp$平面POD,所以点P在坐标平面yOz内,设$\angle POD = \alpha,$$PO = OD =\sqrt{3},$则$P(0,\sqrt{3}\cos\alpha,\sqrt{3}\sin\alpha),$A(1,0,0),$D(0,\sqrt{3},0),$B(-1,0,0),$C(-2,\sqrt{3},0),$$F( - \frac{3}{2},\frac{\sqrt{3}}{2},0),$所以$\overrightarrow{AP} = (-1,\sqrt{3}\cos\alpha,\sqrt{3}\sin\alpha),$$\overrightarrow{DF} =( - \frac{3}{2}, - \frac{\sqrt{3}}{2},0),$$\overrightarrow{AB} = (-2,0,0),$因为直线AP与DF的夹角的余弦值为$\frac{\sqrt{3}}{6},$所以$\frac{|\overrightarrow{AP} · \overrightarrow{DF}|}{|\overrightarrow{AP}||\overrightarrow{DF}|} = \frac{\sqrt{3}}{6},$$\frac{|\frac{3}{2} - \frac{3}{2}\cos\alpha|}{2\sqrt{3}} = \frac{\sqrt{3}}{6},$解得$\cos\alpha = \frac{1}{3},$因为$\alpha \in (0,\pi),$所以$\sin\alpha = \frac{2\sqrt{2}}{3},$得$P(0,\frac{\sqrt{3}}{3},\frac{2\sqrt{6}}{3}),$所以$\overrightarrow{AP} = (-1,\frac{\sqrt{3}}{3},\frac{2\sqrt{6}}{3}),$$\overrightarrow{PC} = (-2,\frac{2\sqrt{3}}{3}, - \frac{2\sqrt{6}}{3}),$设平面PAB的法向量为$\mathbf{n} = (x,y,z),$

则$\begin{cases} \overrightarrow{AP} · \mathbf{n} = - x + \frac{\sqrt{3}}{3}y + \frac{2\sqrt{6}}{3}z = 0 \\\overrightarrow{AB} · \mathbf{n} = -2x = 0 \end{cases},$令$x = 2\sqrt{2},$得$\mathbf{n} = (0,2\sqrt{2}, -1),$记直线PC与平面PAB所成角为$\theta,$则$\sin\theta =$|$\frac{\overrightarrow{PC} · \mathbf{n}}{|\overrightarrow{PC}||\mathbf{n}|}$|$ = \frac{|\frac{2\sqrt{6}}{3}|}{\sqrt{2^{2} × 3} × \sqrt{1 + 8 + 1}} = \frac{\sqrt{3}}{3}.$
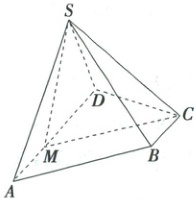
12. (15 分)(2025·江西省萍乡市三模)已知四棱锥 $S - ABCD$ 中,二面角 $S - AD - B$ 为直二面角,$AD = \frac{4}{3}CD = 2SD = 4BC = 4$,$\angle BCD = \angle ADC = \angle ASD = 90^{\circ}$,$M$ 为棱 $DA$ 上一点.
(1)证明:$SA\perp SC$;
(2)若 $M$ 为 $DA$ 中点,求二面角 $B - SC - M$ 的正弦值;
(3)若 $BM//$ 平面 $SCD$,点 $N$ 在平面 $SMB$ 上,若直线 $AN$ 与平面 $SCD$ 所成角为 $\frac{\pi}{6}$,求 $MN$ 的最小值.
(1)证明:$SA\perp SC$;
(2)若 $M$ 为 $DA$ 中点,求二面角 $B - SC - M$ 的正弦值;
(3)若 $BM//$ 平面 $SCD$,点 $N$ 在平面 $SMB$ 上,若直线 $AN$ 与平面 $SCD$ 所成角为 $\frac{\pi}{6}$,求 $MN$ 的最小值.

答案:
12.解:
(1)证明:由$\angle ADC = 90^{\circ}$,得$CD \perp AD$,二面角$S - AD - B$为直二面角,即平面$SAD\perp$平面$ABCD$,而平面$SAD \cap$平面$ABCD = AD$,$CD\subset$平面$ABCD$,故$CD\perp$平面$SAD$.因为$SA\subset$平面$SAD$,所以$SA\perp CD$,又$SA\perp SD$,$SD,CD\subset$平面$SCD$,$SD \capCD = D$,故$SA\perp$平面$SCD$,又$SC\subset$平面$SCD$,故$SA\perp SC$.
(2)过点$S$作$SO\perp AD$于点$O$,连接$OB$,由$\triangle ADS\sim \triangle SDO$,得$OD = 1 = BC$.又$OD// BC$,故四边形$OBCD$为平行四边形,因为$\angle ADC = 90^{\circ}$,所以$\angle DOB = 90^{\circ}$,即$OD\perp OB$,故$OA,OB,OS$两两垂直,以$O$为坐标原点,$OA,OB,OS$所在的直线分别为$x,y,z$轴建立如图所示的空间直角坐标系,则$B(0,3,0)$,$S(0,0,\sqrt{3})$,$C(-1,3,0)$,$D(-1,0,0)$,故$\overrightarrow{BS} = (0,-3,\sqrt{3})$,$\overrightarrow{BC} = (-1,0,0)$,$\overrightarrow{CM} = (2,-3,0)$,$\overrightarrow{SM} = (1,0, - \sqrt{3})$,设平面$SBC$的法向量$\mathbf{a} = (x_{1},y_{1},z_{1})$,则$\begin{cases} \mathbf{a} · \overrightarrow{BS} = - 3y_{1} + \sqrt{3}z_{1} = 0 \\\mathbf{a} · \overrightarrow{BC} = - x_{1} = 0 \end{cases}$,令$y_{1} = 1$,则$z_{1} = \sqrt{3}$,$x_{1} = 0$,故$\mathbf{a} = (0,1,\sqrt{3})$为平面$SBC$的一个法向量,设平面$SCM$的法向量的$\mathbf{b} = (x_{2},y_{2},z_{2})$,则$\begin{cases} \mathbf{b} · \overrightarrow{CM} = 2x_{2} - 3y_{2} = 0 \\\mathbf{b} · \overrightarrow{SM} = x_{2} - \sqrt{3}z_{2} = 0 \end{cases}$,令$z_{2} = \sqrt{3}$,则$x_{2} = 3$,$y_{2} = 2$,故$\mathbf{b} = (3,2,\sqrt{3})$为平面$SCM$的一个法向量,则$\cos\langle\mathbf{a},\mathbf{b}\rangle = \frac{\mathbf{a} · \mathbf{b}}{|\mathbf{a}||\mathbf{b}|} =\frac{0 × 3 + 1 × 2 + \sqrt{3} × \sqrt{3}}{2 × 4} = \frac{5}{8}$,二面角$B - SC - M$的正弦值为$\sqrt{1 - \cos^{2}\langle\mathbf{a},\mathbf{b}\rangle} = \frac{\sqrt{39}}{8}$.
(3)若$BM//$平面$SCD$,$BM\subset$平面$ABCD$,平面$ABCD \cap$平面$SCD = CD$,则$BM// CD$,由
(2)知$OB// DC$,故$M$与$O$点重合,因为$N$在平面$SMB$上,设$N(0,p,t)$,$p,t \in \mathbf{R}$,$A(3,0,0)$,则$\overrightarrow{AN} = (-3,p,t)$,因为$S(0,0,\sqrt{3})$,$C(-1,3,0)$,$D(-1,0,0)$,则$\overrightarrow{SC} = (-1,3, - \sqrt{3})$,$\overrightarrow{SD} = (-1,0, - \sqrt{3})$,设平面$SCD$的法向量$\mathbf{m} = (x,y,z)$,则$\begin{cases} \mathbf{m} · \overrightarrow{SC} = - x + 3y - \sqrt{3}z = 0 \\\mathbf{m} · \overrightarrow{SD} = - x - \sqrt{3}z = 0 \end{cases}$,令$z = \sqrt{3}$,则$x = -3$,$y = 0$,故$\mathbf{m} = (-3,0,\sqrt{3})$为平面$SCD$的一个法向量,故$|\cos\langle\mathbf{m},\overrightarrow{AN}\rangle| = \frac{|\mathbf{m} · \overrightarrow{AN}|}{|\mathbf{m}||\overrightarrow{AN}|} =\frac{|9 + \sqrt{3}t|}{\sqrt{12} × \sqrt{9 + p^{2} + t^{2}}} = \frac{1}{2}$,整理得$p^{2} - 6\sqrt{3}t - 18 = 0$,又$p^{2} = 6\sqrt{3}t + 18 \geqslant 0$,故$t \geqslant - \sqrt{3}$,由$\overrightarrow{MN} = (0,p,t)$,故$|\overrightarrow{MN}| = \sqrt{p^{2} + t^{2}} = \sqrt{t^{2} + 6\sqrt{3}t + 18} = \sqrt{(t + 3\sqrt{3})^{2} - 9}\geqslant \sqrt{3}$,当且仅当$t = - \sqrt{3}$时等号成立,

MN取得最小值为$\sqrt{3}$.
12.解:
(1)证明:由$\angle ADC = 90^{\circ}$,得$CD \perp AD$,二面角$S - AD - B$为直二面角,即平面$SAD\perp$平面$ABCD$,而平面$SAD \cap$平面$ABCD = AD$,$CD\subset$平面$ABCD$,故$CD\perp$平面$SAD$.因为$SA\subset$平面$SAD$,所以$SA\perp CD$,又$SA\perp SD$,$SD,CD\subset$平面$SCD$,$SD \capCD = D$,故$SA\perp$平面$SCD$,又$SC\subset$平面$SCD$,故$SA\perp SC$.
(2)过点$S$作$SO\perp AD$于点$O$,连接$OB$,由$\triangle ADS\sim \triangle SDO$,得$OD = 1 = BC$.又$OD// BC$,故四边形$OBCD$为平行四边形,因为$\angle ADC = 90^{\circ}$,所以$\angle DOB = 90^{\circ}$,即$OD\perp OB$,故$OA,OB,OS$两两垂直,以$O$为坐标原点,$OA,OB,OS$所在的直线分别为$x,y,z$轴建立如图所示的空间直角坐标系,则$B(0,3,0)$,$S(0,0,\sqrt{3})$,$C(-1,3,0)$,$D(-1,0,0)$,故$\overrightarrow{BS} = (0,-3,\sqrt{3})$,$\overrightarrow{BC} = (-1,0,0)$,$\overrightarrow{CM} = (2,-3,0)$,$\overrightarrow{SM} = (1,0, - \sqrt{3})$,设平面$SBC$的法向量$\mathbf{a} = (x_{1},y_{1},z_{1})$,则$\begin{cases} \mathbf{a} · \overrightarrow{BS} = - 3y_{1} + \sqrt{3}z_{1} = 0 \\\mathbf{a} · \overrightarrow{BC} = - x_{1} = 0 \end{cases}$,令$y_{1} = 1$,则$z_{1} = \sqrt{3}$,$x_{1} = 0$,故$\mathbf{a} = (0,1,\sqrt{3})$为平面$SBC$的一个法向量,设平面$SCM$的法向量的$\mathbf{b} = (x_{2},y_{2},z_{2})$,则$\begin{cases} \mathbf{b} · \overrightarrow{CM} = 2x_{2} - 3y_{2} = 0 \\\mathbf{b} · \overrightarrow{SM} = x_{2} - \sqrt{3}z_{2} = 0 \end{cases}$,令$z_{2} = \sqrt{3}$,则$x_{2} = 3$,$y_{2} = 2$,故$\mathbf{b} = (3,2,\sqrt{3})$为平面$SCM$的一个法向量,则$\cos\langle\mathbf{a},\mathbf{b}\rangle = \frac{\mathbf{a} · \mathbf{b}}{|\mathbf{a}||\mathbf{b}|} =\frac{0 × 3 + 1 × 2 + \sqrt{3} × \sqrt{3}}{2 × 4} = \frac{5}{8}$,二面角$B - SC - M$的正弦值为$\sqrt{1 - \cos^{2}\langle\mathbf{a},\mathbf{b}\rangle} = \frac{\sqrt{39}}{8}$.
(3)若$BM//$平面$SCD$,$BM\subset$平面$ABCD$,平面$ABCD \cap$平面$SCD = CD$,则$BM// CD$,由
(2)知$OB// DC$,故$M$与$O$点重合,因为$N$在平面$SMB$上,设$N(0,p,t)$,$p,t \in \mathbf{R}$,$A(3,0,0)$,则$\overrightarrow{AN} = (-3,p,t)$,因为$S(0,0,\sqrt{3})$,$C(-1,3,0)$,$D(-1,0,0)$,则$\overrightarrow{SC} = (-1,3, - \sqrt{3})$,$\overrightarrow{SD} = (-1,0, - \sqrt{3})$,设平面$SCD$的法向量$\mathbf{m} = (x,y,z)$,则$\begin{cases} \mathbf{m} · \overrightarrow{SC} = - x + 3y - \sqrt{3}z = 0 \\\mathbf{m} · \overrightarrow{SD} = - x - \sqrt{3}z = 0 \end{cases}$,令$z = \sqrt{3}$,则$x = -3$,$y = 0$,故$\mathbf{m} = (-3,0,\sqrt{3})$为平面$SCD$的一个法向量,故$|\cos\langle\mathbf{m},\overrightarrow{AN}\rangle| = \frac{|\mathbf{m} · \overrightarrow{AN}|}{|\mathbf{m}||\overrightarrow{AN}|} =\frac{|9 + \sqrt{3}t|}{\sqrt{12} × \sqrt{9 + p^{2} + t^{2}}} = \frac{1}{2}$,整理得$p^{2} - 6\sqrt{3}t - 18 = 0$,又$p^{2} = 6\sqrt{3}t + 18 \geqslant 0$,故$t \geqslant - \sqrt{3}$,由$\overrightarrow{MN} = (0,p,t)$,故$|\overrightarrow{MN}| = \sqrt{p^{2} + t^{2}} = \sqrt{t^{2} + 6\sqrt{3}t + 18} = \sqrt{(t + 3\sqrt{3})^{2} - 9}\geqslant \sqrt{3}$,当且仅当$t = - \sqrt{3}$时等号成立,

MN取得最小值为$\sqrt{3}$.
查看更多完整答案,请扫码查看


