《2026年一本密卷高考数学》

16. (15分) 浙里启航团队举办了一场抽奖游戏, 玩家一共抽取 $ n $ 次. 每次都有 $ \frac{1}{2} $ 的概率抽中, $ \frac{1}{2} $ 的概率没抽中. 小明的抽奖得分按照如下方式计算:
1. 将玩家 $ n $ 次抽奖的结果按顺序排列, 抽中记作 $ 1 $, 未抽中记作 $ 0 $, 形成一个长度为 $ n $ 的仅有 $ 01 $ 的序列.
2. 定义序列的得分为: 对于这个序列每一段极长连续的 $ 1 $, 设它长度为 $ t $, 那么得分即为 $ t^2 $.
3. 序列的得分即为每一段连续的 $ 1 $ 的得分和.
例如: 如果玩家 $ A $ 抽了 $ 7 $ 次, 第 $ 1, 3, 4, 5, 7 $ 次中奖, 那么序列即为 $ 1, 0, 1, 1, 1, 0, 1 $, 得分为 $ 1^2 + 3^2 + 1^2 = 11 $. 可能用到的公式: 若 $ X, Y $ 为两个随机变量, 则 $ E(X) + E(Y) = E(X + Y) $.
(1) 若 $ n = 3 $, 清照进行了一次游戏. 记随机变量 $ X $ 为清照的最终得分, 求 $ E(X) $;
(2) 记随机变量 $ Z $ 表示长度为 $ n $ 的序列中从最后一个数从后往前极长连续的 $ 1 $ 的长度, 求 $ E(Z) $;
(3) 若 $ n = k $, 清照进行了一次游戏. 记随机变量 $ A $ 为清照的最终得分, 求 $ E(A) $.

答案： 16.解：（1）若序列为$0,0,0$，则最终得分为$0$，若序列为$1,0,0$，或$0,1,0$，或$0,0,1$，则最终得分为$1$，若序列为$1,0,1$，则最终得分为$2$，若序列为$1,1,0$，或$0,1,1$，则最终得分为$4$，若序列为$1,1,1$，则最终得分为$9$，$P(X = 0)=\frac{1}{8}$，$P(X = 1)=\frac{3}{8}$，$P(X = 2)=\frac{1}{8}$，$P(X = 4)=\frac{1}{4}$，$P(X = 9)=\frac{1}{8}$，$E(X)=0×\frac{1}{8}+1×\frac{3}{8}+2×\frac{1}{8}+4×\frac{1}{4}+9×\frac{1}{8}=\frac{11}{4}$.
（2）令$g_n$表示长度为$n$的序列，$E(Z)$的答案，换言之$E(Z)=g_n$，则有递推关系$g_{n + 1}=\frac{1}{2}·(g_n + 1 + 0)$，表示第$n + 1$位分别为$1$或$0$的答案.显然$g_1=\frac{1}{2}×(0 + 1)=\frac{1}{2}$，设$g_{n + 1}+\lambda=\frac{1}{2}·(g_n+\lambda)$，则$g_{n + 1}=g_n-\frac{1}{2}\lambda$，所以$-\frac{1}{2}\lambda=\frac{1}{2}$，解得$\lambda=-1$，所以$g_n - 1=(g_1 - 1)(\frac{1}{2})^{n - 1}=-\frac{1}{2^n}$，解得$g_n = 1-\frac{1}{2^n}$，故所求为$1-\frac{1}{2^n}$.
（3）设$f_n$表示进行$n$次游戏后的期望得分，即$E(A)=f_n$，则有递推关系$f_n=f_{n - 1}+\frac{1}{2}(1 + 2× g_{n - 1})$，$(n\geq1,n\in N^*)$，解释：因为$(x + 1)^2=x^2+2x + 1$，考虑第$n$位为$1$的时候对序列的额外贡献，即为$(g_{n - 1}+1)^2 - g_{n - 1}^2=2g_{n - 1}+1$，如果为$0$的贡献即为$0$，特别的，$f_0 = 0$，直接累加得到：$f_n=\frac{n}{2}+(g_0 + g_1+·s+g_{n - 1})=\frac{n}{2}-\frac{1}{2}[1 - (\frac{1}{2})^n]+(n - 1)+\frac{3n - 4}{2}+\frac{1}{2^{n - 1}}$，若$n = k$，带入上式，于是得$f_k=\frac{3k - 4}{2}+\frac{1}{2^{k - 1}}$，故所求即为$\frac{3k - 4}{2}+\frac{1}{2^{k - 1}}$.

17. (15分) 已知: 斜三棱柱 $ ABC - A_1B_1C_1 $ 中, $ BB_1 \perp AC $, $ AA_1 $ 与面 $ ABC $ 所成角正切值为 $ 2 $, $ AA_1 = \sqrt{5} $, $ AB = BC = \frac{\sqrt{2}}{2}AC = 2\sqrt{2} $, 点 $ E $ 为棱 $ A_1C_1 $ 的中点, 且点 $ E $ 向平面 $ ABC $ 所作投影在 $ \triangle ABC $ 内.

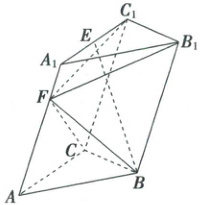
(1) 求证: $ AC \perp EB $;
(2) $ F $ 为棱 $ AA_1 $ 上一点, 且二面角 $ A - BC - F $ 为 $ 30° $, 求 $ \frac{AF}{AA_1} $ 的值.

答案：
17.解：（1）证明：取线段$AC$的中点$M$，连接$EM$、$BM$，在斜三棱柱$ABC - A_1B_1C_1$中，$AA_1// CC_1$且$AA_1 = CC_1$，则四边形$AA_1C_1C$为平行四边形，所以$AC// A_1C_1$且$AC = A_1C_1$，因为$E$、$M$分别为$A_1C_1$、$AC$的中点，则四边形$AA_1EM$为平行四边形，所以$EM// AA_1$，又因为$AA_1// BB_1$，则$EM// BB_1$，因为$AC\perp BB_1$，则$AC\perp EM$，因为$AB = BC$，$M$为$AC$的中点，则$BM\perp AC$，因为$EM\cap BM = M$，$EM$、$BM\subset$平面$BEM$，所以$AC\perp$平面$BEM$，因为$EB\subset$平面$BEM$，所以$EB\perp AC$.
（2）由（1）可知，$AC\perp$平面$EMB$，过点$E$在平面$BB_1EM$内作$EO\perp BM$，垂足为点$O$，因为$AC\perp$平面$BB_1EM$，$EO\subset$平面$BB_1EM$，则$EO\perp AC$，又因为$EO\perp BM$，$BM\cap AC = M$，$BM$、$AC\subset$平面$ABC$，则$EO\perp$平面$ABC$，所以直线$AA_1$与平面$ABC$所成的角为$\angle EMO$，所以$\tan\angle EMO=\frac{EO}{OM}=2$，则$EO = 2OM$，因为$EM=\sqrt{EO^2 + OM^2}=\sqrt{5}OM=\sqrt{5}$，可得$OM = 1$，$EO = 2$，因为$AB = BC=\frac{\sqrt{2}}{2}AC = 2\sqrt{2}$，则$AB^2 + BC^2 = AC^2$，则$AB\perp BC$，因为$M$为$AC$的中点，所以，$MB=\frac{1}{2}AC = 2$，以点$O$为坐标原点，$Ox$、$OB$、$OE$的方向分别为$x$、$y$、$z$轴的正方向建立如下图所示的空间直角坐标系，

则$A(2,-1,0)$、$B(0,1,0)$、$M(0,-1,0)$、$C(-2,-1,0)$、$E(0,0,2)$，$\overrightarrow{ME}=(0,1,2)$，则$\overrightarrow{OA_1}=\overrightarrow{OA}+\overrightarrow{AA_1}=\overrightarrow{OA}+\overrightarrow{ME}=(2,-1,0)+(0,1,2)=(2,0,2)$，同理可得点$B_1(0,2,2)$、$C_1(-2,0,2)$，设$\overrightarrow{AF}=\lambda\overrightarrow{AA_1}=\lambda(0,1,2)=(0,\lambda,2\lambda)$，其中$0\leq\lambda\leq1$，则$\overrightarrow{CF}=\overrightarrow{CA}+\overrightarrow{AF}=(4,0,0)+(0,\lambda,2\lambda)=(4,\lambda,2\lambda)$，且$\overrightarrow{CB}=(2,2,0)$，设平面$BCF$的法向量为$\mathbf{m}=(x,y,z)$，则$\begin{cases}\mathbf{m}·\overrightarrow{CB}=2x + 2y = 0\\\mathbf{m}·\overrightarrow{CF}=4x+\lambda y + 2\lambda z = 0\end{cases}$取$x = 2\lambda$，则$y = -2\lambda$，$z=\lambda - 4$，所以平面$BCF$的一个法向量为$\mathbf{m}=(2\lambda,-2\lambda,\lambda - 4)$，易知平面$ABC$的一个法向量为$\mathbf{n}=(0,0,1)$，因为二面角$A - BC - F$为$30°$，则$|\cos\langle\mathbf{m},\mathbf{n}\rangle|=\frac{|\mathbf{m}·\mathbf{n}|}{|\mathbf{m}|·|\mathbf{n}|}=\frac{|\lambda - 4|}{\sqrt{4\lambda^2 + 4\lambda^2+(\lambda - 4)^2}}=\frac{\sqrt{3}}{2}$，整理可得$23\lambda^2 + 8\lambda - 16 = 0$，因为$0\leq\lambda\leq1$，解得$\lambda=\frac{8\sqrt{6}-4}{23}$，即$\frac{AF}{AA_1}=\frac{8\sqrt{6}-4}{23}$.