《2026年一本密卷高考数学》

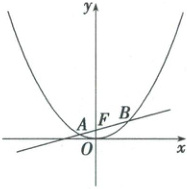
12. （15 分）（2025·四川省成都市三模）如图，在直角坐标系 $ xOy $ 中，已知 $ F $ 是抛物线 $ \Gamma:x^2 = 2py(p ＞ 0) $ 的焦点，过点 $ F $ 的直线交抛物线 $ \Gamma $ 于 $ A $，$ B $ 两点，且满足 $ \overrightarrow{OA} · \overrightarrow{OB} = -3 $。
（1）求 $ p $ 的值；
（2）已知点 $ T(0,3) $，直线 $ AT $，$ BT $ 与抛物线 $ \Gamma $ 的另一个交点分别为 $ C $，$ D $，直线 $ CD $ 交 $ y $ 轴于点 $ P $，交直线 $ AB $ 于点 $ N $。抛物线 $ \Gamma $ 在 $ C $，$ D $ 处的切线交于点 $ K $，过点 $ P $ 作平行于 $ x $ 轴的直线，分别交直线 $ KD $，$ KC $ 于点 $ E $，$ G $。
（ⅰ）求证：点 $ P $ 为定点；
（ⅱ）记 $ \triangle ENK $，$ \triangle GNK $ 的面积分别为 $ S_1 $，$ S_2 $，求 $ S_1 + S_2 $ 的最小值。

答案：
12.解：
(1)由题意，直线$AB$斜率必存在，设$AB:y = kx+\frac{p}{2}$，$A(x_1,y_1)$，$B(x_2,y_2)$，联立$\begin{cases}y = kx+\frac{p}{2}\\x^2 = 2py\end{cases}$，得$x^2 - 2pkx - p^2 = 0$，$\Delta = 4p^2(k^2 + 1)＞0$。所以$x_1 + x_2 = 2pk$，$x_1x_2 = -p^2$。由$\overrightarrow{OA}·\overrightarrow{OB}=x_1x_2 + y_1y_2=x_1x_2+\frac{1}{4p^2}· x_1^2· x_2^2=-p^2+\frac{p^2}{4}=-3$，解得$p = 2$或$p = -2$(舍)。所以$p = 2$。
(2)(i)证明：直线$AC$斜率必存在，设$AC:y = k_1x + 3$，$C(x_3,y_3)$，$D(x_4,y_4)$，联立$\begin{cases}x^2 = 4y\\y = k_1x + 3\end{cases}$，得$x^2 - 4k_1x - 12 = 0$，所以$x_1x_3 = -12$，同理$x_2x_4 = -12$。又因为$x_1x_2 = -4$，所以$x_3x_4 = -36$。直线$CD$斜率必存在，设$CD:y = k_2x + m$，联立$\begin{cases}x^2 = 4y\\y = k_2x + m\end{cases}$，得$x^2 - 4k_2x - 4m = 0$，所以$x_3x_4 = -4m = -36$，解得$m = 9$，所以直线$CD$过定点$(0,9)$。即$P$的坐标为$(0,9)$。
(ii)由$k_{CD}=\frac{y_3 - y_4}{x_3 - x_4}=\frac{x_3 + x_4}{4}=\frac{1}{4}(\frac{-12}{x_1}+\frac{12}{x_2})=\frac{3}{4}(\frac{x_2 - x_1}{x_1x_2})=3k$，所以直线$CD$的方程为$y = 3kx + 9$。由直线$CD$与直线$AB$相交，可得$k\neq0$。联立$\begin{cases}y = 3kx + 9\\y = kx + 1\end{cases}$解得$N(-\frac{4}{k},-3)$。因为抛物线方程为$y=\frac{x^2}{4}$，所以$y'=\frac{x}{2}$，抛物线在点$C$处切线方程为$y=\frac{x_3}{2}(x - x_3)+y_3=\frac{x_3}{2}x-\frac{1}{4}x_3^2$，所以$E(\frac{18}{x_3}+\frac{x_3}{2},9)$，同理$G(\frac{18}{x_4}+\frac{x_4}{2},9)$。又$\frac{18}{x_3}+\frac{x_3}{2}+\frac{18}{x_4}+\frac{x_4}{2}=\frac{18(x_3 + x_4)}{x_3x_4}+\frac{x_3 + x_4}{2}=0$，所以$EG$的中点为$P$。联立$\begin{cases}y=\frac{x_4}{2}x-\frac{1}{4}x_4^2\\y=\frac{x_3}{2}x-\frac{1}{4}x_3^2\end{cases}$，得$K(\frac{x_3 + x_4}{2},\frac{x_3x_4}{4})$，由$x_3 + x_4 = 3(x_1 + x_2)$及$x_3x_4 = -36$，所以$K(6k,-9)$。过$N$作平行于$x$轴的直线交$PK$于点$H$，则$H(4k,-3)$。所以$S_1 + S_2 = 2S_{\triangle PNK}=|HN|·(y_P - y_K)=|x_N - x_H|·(y_P - y_K)=18|4k+\frac{4}{k}|=72(|k|+\frac{1}{|k|})\geq144\sqrt{|k|·\frac{1}{|k|}}=144$。当且仅当$|k| = 1$时，即直线$AB$方程为$y = x + 1$或$y = -x + 1$时等号成立。