2026年一本密卷高考数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年一本密卷高考数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
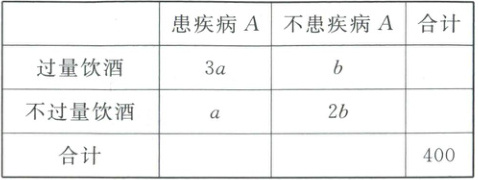
9. 某研究机构为了探究过量饮酒与患疾病 $ A $ 是否有关,调查了400人,得到如图所示的 $ 2 × 2 $ 列联表,其中 $ b = 12a $,则(
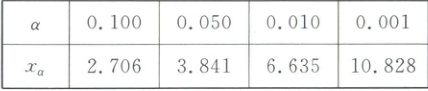
参考公式与临界值表:$ \chi^2 = \frac{n(ad - bc)^2}{(a + b)(c + d)(a + c)(b + d)} $
A.任意一人不患疾病 $ A $ 的概率为0.9
B.任意一人不过量饮酒的概率为 $ \frac{3}{8} $
C.任意一人在不过量饮酒的条件下不患疾病 $ A $ 的概率为 $ \frac{24}{25} $
D.依据小概率值 $ \alpha = 0.001 $ 的独立性检验,认为过量饮酒与患疾病 $ A $ 有关
ACD
)
参考公式与临界值表:$ \chi^2 = \frac{n(ad - bc)^2}{(a + b)(c + d)(a + c)(b + d)} $

A.任意一人不患疾病 $ A $ 的概率为0.9
B.任意一人不过量饮酒的概率为 $ \frac{3}{8} $
C.任意一人在不过量饮酒的条件下不患疾病 $ A $ 的概率为 $ \frac{24}{25} $
D.依据小概率值 $ \alpha = 0.001 $ 的独立性检验,认为过量饮酒与患疾病 $ A $ 有关
答案:
9.ACD 由已知得$4a + 3b = 400$,又$b = 12a$,所以$a = 10$,$b = 120$。
任意一人不患疾病$A$的概率为$\frac{3b}{400} = 0.9$,所以$A$正确;
任意一人不过量饮酒的概率为$\frac{a + 2b}{400} = \frac{5}{8}$,所以$B$错误;
任意一人在不过量饮酒的条件下不患疾病$A$的概率为$\frac{2b}{a + 2b} = \frac{24}{25}$,
所以$C$正确;
对于$D$,$2 × 2$列联表如下:
| | 患疾病$A$ | 不患疾病$A$ | 合计 |
| --- | --- | --- | --- |
| 过量饮酒 | 30 | 120 | 150 |
| 不过量饮酒 | 10 | 240 | 250 |
| 合计 | 40 | 360 | 400 |
则$\chi^2$的观测值$\chi^2 = \frac{400 × (30 × 240 - 120 × 10)^2}{40 × 360 × 150 × 250} = \frac{80}{3} \approx 26.67$,由于$26.67 > 10.828$,
依据小概率值$\alpha = 0.001$的独立性检验,认为过量饮酒与患疾病$A$有关,所以$D$正确。
故选:ACD。
任意一人不患疾病$A$的概率为$\frac{3b}{400} = 0.9$,所以$A$正确;
任意一人不过量饮酒的概率为$\frac{a + 2b}{400} = \frac{5}{8}$,所以$B$错误;
任意一人在不过量饮酒的条件下不患疾病$A$的概率为$\frac{2b}{a + 2b} = \frac{24}{25}$,
所以$C$正确;
对于$D$,$2 × 2$列联表如下:
| | 患疾病$A$ | 不患疾病$A$ | 合计 |
| --- | --- | --- | --- |
| 过量饮酒 | 30 | 120 | 150 |
| 不过量饮酒 | 10 | 240 | 250 |
| 合计 | 40 | 360 | 400 |
则$\chi^2$的观测值$\chi^2 = \frac{400 × (30 × 240 - 120 × 10)^2}{40 × 360 × 150 × 250} = \frac{80}{3} \approx 26.67$,由于$26.67 > 10.828$,
依据小概率值$\alpha = 0.001$的独立性检验,认为过量饮酒与患疾病$A$有关,所以$D$正确。
故选:ACD。
10. 已知函数 $ f(x) = \sin 2x + m\cos 2x (m > 0) $ 的最大值为2,则(
A.$ m = \sqrt{3} $
B.函数 $ f(x) $ 图象的一个对称中心是点 $ \left( \frac{5\pi}{6}, 0 \right) $
C.$ f(x) $ 在区间 $ \left( \frac{4\pi}{3}, \frac{3\pi}{2} \right) $ 上单调递增
D.将 $ f(x) $ 的图象先向右平移 $ \frac{\pi}{3} $ 个单位长度后,再将图象上所有点的横坐标伸长为原来的两倍(纵坐标不变),得到的图象对应的函数解析式为 $ g(x) = 2\sin 4x $
AB
)A.$ m = \sqrt{3} $
B.函数 $ f(x) $ 图象的一个对称中心是点 $ \left( \frac{5\pi}{6}, 0 \right) $
C.$ f(x) $ 在区间 $ \left( \frac{4\pi}{3}, \frac{3\pi}{2} \right) $ 上单调递增
D.将 $ f(x) $ 的图象先向右平移 $ \frac{\pi}{3} $ 个单位长度后,再将图象上所有点的横坐标伸长为原来的两倍(纵坐标不变),得到的图象对应的函数解析式为 $ g(x) = 2\sin 4x $
答案:
10.AB 对于$A$,因为$f(x) = \sin 2x + m\cos 2x = \sqrt{1 + m^2}\sin(2x + \varphi)$(其中$\tan \varphi = m$),且函数$f(x)$的最大值为$2$,所以$\sqrt{1 + m^2} = 2$,解得$m = \pm \sqrt{3}$,
又因为$m > 0$,所以$m = \sqrt{3}$,故$A$正确;
对于$B$,方法一:由$A$选项可知,$f(x) = \sin 2x + \sqrt{3}\cos 2x = 2\sin(2x + \frac{\pi}{3})$,
令$2x + \frac{\pi}{3} = k\pi(k \in \mathbf{Z})$,
解得$x = \frac{k\pi}{2} - \frac{\pi}{6}(k \in \mathbf{Z})$,
当$k = 2$时,$x = \frac{5\pi}{6}$,所以$f(x)$的图象关于点$(\frac{5\pi}{6}, 0)$中心对称,故$B$正确;
方法二:由$A$选项可知,$f(x) = \sin 2x + \sqrt{3}\cos 2x = 2\sin(2x + \frac{\pi}{3})$,
将$x = \frac{5\pi}{6}$代入$f(x)$的解析式,
得$2\sin(2 × \frac{5\pi}{6} + \frac{\pi}{3}) = 2\sin 2\pi = 0$,
所以$f(x)$的图象关于点$(\frac{5\pi}{6}, 0)$中心对称,故$B$正确;
对于$C$,当$x \in (\frac{4\pi}{3}, \frac{3\pi}{2})$时,
$2x + \frac{\pi}{3} \in (3\pi, \frac{10\pi}{3}) \subseteq [\frac{5\pi}{2}, \frac{7\pi}{2}]$,根据正弦函数的图象得$f(x)$在$(\frac{4\pi}{3}, \frac{3\pi}{2})$上单调递减,故$C$错误;
对于$D$,将$f(x)$的图象先向右平移$\frac{\pi}{3}$个单位长度,得到
$y = 2\sin[2(x - \frac{\pi}{3}) + \frac{\pi}{3}] = 2\sin(2x - \frac{\pi}{3})$的图象,
再将图象上所有点的横坐标伸长为原来的两倍,得到$g(x) = 2\sin(x - \frac{\pi}{3})$的图象,故$D$错误。故选$AB$。
又因为$m > 0$,所以$m = \sqrt{3}$,故$A$正确;
对于$B$,方法一:由$A$选项可知,$f(x) = \sin 2x + \sqrt{3}\cos 2x = 2\sin(2x + \frac{\pi}{3})$,
令$2x + \frac{\pi}{3} = k\pi(k \in \mathbf{Z})$,
解得$x = \frac{k\pi}{2} - \frac{\pi}{6}(k \in \mathbf{Z})$,
当$k = 2$时,$x = \frac{5\pi}{6}$,所以$f(x)$的图象关于点$(\frac{5\pi}{6}, 0)$中心对称,故$B$正确;
方法二:由$A$选项可知,$f(x) = \sin 2x + \sqrt{3}\cos 2x = 2\sin(2x + \frac{\pi}{3})$,
将$x = \frac{5\pi}{6}$代入$f(x)$的解析式,
得$2\sin(2 × \frac{5\pi}{6} + \frac{\pi}{3}) = 2\sin 2\pi = 0$,
所以$f(x)$的图象关于点$(\frac{5\pi}{6}, 0)$中心对称,故$B$正确;
对于$C$,当$x \in (\frac{4\pi}{3}, \frac{3\pi}{2})$时,
$2x + \frac{\pi}{3} \in (3\pi, \frac{10\pi}{3}) \subseteq [\frac{5\pi}{2}, \frac{7\pi}{2}]$,根据正弦函数的图象得$f(x)$在$(\frac{4\pi}{3}, \frac{3\pi}{2})$上单调递减,故$C$错误;
对于$D$,将$f(x)$的图象先向右平移$\frac{\pi}{3}$个单位长度,得到
$y = 2\sin[2(x - \frac{\pi}{3}) + \frac{\pi}{3}] = 2\sin(2x - \frac{\pi}{3})$的图象,
再将图象上所有点的横坐标伸长为原来的两倍,得到$g(x) = 2\sin(x - \frac{\pi}{3})$的图象,故$D$错误。故选$AB$。
11. 已知双曲线 $ C: \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 (a > 0, b > 0) $ 的一条渐近线 $ l_1 $ 过点 $ P(\sqrt{2}, 1) $,$ F $ 为 $ C $ 的右焦点,则下列关于双曲线 $ C $ 的结论正确的是(
A.离心率为 $ \frac{\sqrt{5}}{2} $
B.两条渐近线的夹角的余弦值为 $ \frac{1}{3} $
C.若直线 $ PF $ 与双曲线 $ C $ 的一条渐近线垂直,则 $ \triangle POF $ 的面积为 $ \frac{3\sqrt{2}}{4} $
D.若 $ F(\sqrt{3}, 0) $,双曲线上一点 $ Q $ 到渐近线 $ l_1 $ 的距离为 $ \frac{1}{3} $,则点 $ Q $ 到另一条渐近线 $ l_2 $ 的距离为2
BD
)A.离心率为 $ \frac{\sqrt{5}}{2} $
B.两条渐近线的夹角的余弦值为 $ \frac{1}{3} $
C.若直线 $ PF $ 与双曲线 $ C $ 的一条渐近线垂直,则 $ \triangle POF $ 的面积为 $ \frac{3\sqrt{2}}{4} $
D.若 $ F(\sqrt{3}, 0) $,双曲线上一点 $ Q $ 到渐近线 $ l_1 $ 的距离为 $ \frac{1}{3} $,则点 $ Q $ 到另一条渐近线 $ l_2 $ 的距离为2
答案:
11.BD 对于$A$,根据题意,渐近线$l_1$的斜率$k_1 = \frac{b}{a} = \frac{1}{\sqrt{2}}$,
则离心率$e = \frac{c}{a} = \sqrt{1 + \frac{b^2}{a^2}} = \sqrt{1 + (\frac{1}{\sqrt{2}})^2} = \frac{\sqrt{6}}{2}$,故$A$错误;
对于$B$,设渐近线$l_1$的倾斜角为$\theta$,则$\tan \theta = \frac{1}{\sqrt{2}} < 1$,所以$0 < \theta < \frac{\pi}{4}$,则两条渐近线的夹角为$2\theta$,
所以$\tan 2\theta = \frac{2\tan \theta}{1 - \tan^2 \theta} = \frac{2×\frac{1}{\sqrt{2}}}{1 - \frac{1}{2}} = 2\sqrt{2}$,
所以$\cos 2\theta = \frac{1}{3}$,故$B$正确;
对于$C$,若直线$PF$与双曲线$C$的一条渐近线垂直,则直线$PF$的斜率$k = \pm \sqrt{2}$,则直线$PF$的方程为$y = -\sqrt{2}(x - \sqrt{2}) + 1 = -\sqrt{2}x + 3$或$y = \sqrt{2}(x - \sqrt{2}) + 1 = \sqrt{2}x - 1$,
所以$F(\frac{3\sqrt{2}}{2}, 0)$或$F(\frac{\sqrt{2}}{2}, 0)$,
则$\triangle POF$的面积为$S = \frac{1}{2}\mid OF\mid · y_P = \frac{1}{2} × \frac{3\sqrt{2}}{2} × 1 = \frac{3\sqrt{2}}{4}$或$S = \frac{1}{2}\mid OF\mid · y_P = \frac{1}{2} × \frac{\sqrt{2}}{2} × 1 = \frac{\sqrt{2}}{4}$,
故$C$错误;
对于$D$,由$A$选项可得,双曲线$C$的离心率$e = \frac{\sqrt{6}}{2}$,又$c = \sqrt{3}$,则$a = \sqrt{2}$、$b = 1$,
所以双曲线$C$的方程为$\frac{x^2}{2} - y^2 = 1$,设$Q(x_0, y_0)$,
则$\frac{x_0^2}{2} - y_0^2 = 1$,即$x_0^2 - 2y_0^2 = 2$,
双曲线$C$的两条渐近线方程为$x \pm \sqrt{2}y = 0$,则点$Q$到两渐近线的距离之积
$d_1d_2 = \frac{\mid x_0 + \sqrt{2}y_0\mid}{\sqrt{3}} · \frac{\mid x_0 - \sqrt{2}y_0\mid}{\sqrt{3}} = \frac{\mid x_0^2 - 2y_0^2\mid}{3} = \frac{2}{3}$,因为$d_1 = \frac{1}{3}$,所以$d_2 = 2$,故$D$正确。故选$BD$。
则离心率$e = \frac{c}{a} = \sqrt{1 + \frac{b^2}{a^2}} = \sqrt{1 + (\frac{1}{\sqrt{2}})^2} = \frac{\sqrt{6}}{2}$,故$A$错误;
对于$B$,设渐近线$l_1$的倾斜角为$\theta$,则$\tan \theta = \frac{1}{\sqrt{2}} < 1$,所以$0 < \theta < \frac{\pi}{4}$,则两条渐近线的夹角为$2\theta$,
所以$\tan 2\theta = \frac{2\tan \theta}{1 - \tan^2 \theta} = \frac{2×\frac{1}{\sqrt{2}}}{1 - \frac{1}{2}} = 2\sqrt{2}$,
所以$\cos 2\theta = \frac{1}{3}$,故$B$正确;
对于$C$,若直线$PF$与双曲线$C$的一条渐近线垂直,则直线$PF$的斜率$k = \pm \sqrt{2}$,则直线$PF$的方程为$y = -\sqrt{2}(x - \sqrt{2}) + 1 = -\sqrt{2}x + 3$或$y = \sqrt{2}(x - \sqrt{2}) + 1 = \sqrt{2}x - 1$,
所以$F(\frac{3\sqrt{2}}{2}, 0)$或$F(\frac{\sqrt{2}}{2}, 0)$,
则$\triangle POF$的面积为$S = \frac{1}{2}\mid OF\mid · y_P = \frac{1}{2} × \frac{3\sqrt{2}}{2} × 1 = \frac{3\sqrt{2}}{4}$或$S = \frac{1}{2}\mid OF\mid · y_P = \frac{1}{2} × \frac{\sqrt{2}}{2} × 1 = \frac{\sqrt{2}}{4}$,
故$C$错误;
对于$D$,由$A$选项可得,双曲线$C$的离心率$e = \frac{\sqrt{6}}{2}$,又$c = \sqrt{3}$,则$a = \sqrt{2}$、$b = 1$,
所以双曲线$C$的方程为$\frac{x^2}{2} - y^2 = 1$,设$Q(x_0, y_0)$,
则$\frac{x_0^2}{2} - y_0^2 = 1$,即$x_0^2 - 2y_0^2 = 2$,
双曲线$C$的两条渐近线方程为$x \pm \sqrt{2}y = 0$,则点$Q$到两渐近线的距离之积
$d_1d_2 = \frac{\mid x_0 + \sqrt{2}y_0\mid}{\sqrt{3}} · \frac{\mid x_0 - \sqrt{2}y_0\mid}{\sqrt{3}} = \frac{\mid x_0^2 - 2y_0^2\mid}{3} = \frac{2}{3}$,因为$d_1 = \frac{1}{3}$,所以$d_2 = 2$,故$D$正确。故选$BD$。
12. 各项均为正数的等差数列 $ \{ a_n \} $ 的前 $ n $ 项和为 $ S_n $,若 $ S_9 = 72 $,则 $ a_2a_8 $ 的最大值为
64
.
答案:
12.64 方法一:因为$S_9 = \frac{(a_1 + a_9) × 9}{2} = \frac{2a_5 × 9}{2} = 9a_5 = 72$,所以$a_5 = 8$,
所以$a_2 + a_8 = 2a_5 = 16$,
因为$16 = a_2 + a_8 \geq 2\sqrt{a_2a_8}$,即$\frac{1}{2}(\sqrt{a_2a_8})^2 + 2\sqrt{a_2a_8} - 16 \leq 0$,
所以$\frac{1}{2}(\sqrt{a_2a_8} + 6)(\sqrt{a_2a_8} - 2) \leq 0$,所以$-6 \leq \sqrt{a_2a_8} \leq 2$,
又因为$\sqrt{a_2a_8} > 0$,所以$0 < \sqrt{a_2a_8} \leq 2$,当且仅当$a_2 = a_8 = 8$时取等号。
所以$a_2a_8 \leq 64$,当且仅当$a_2 = a_8 = 8$时取等号。
方法二:因为$S_9 = \frac{(a_1 + a_9) × 9}{2} = \frac{2a_5 × 9}{2} = 9a_5 = 72$,
所以$a_5 = 8$,所以$a_2 + a_8 = 2a_5 = 16$,
则$a_2a_8 = a_2(16 - a_2) = -a_2^2 + 16a_2 = -(a_2 - 8)^2 + 64$,
故当$a_2 = 8$时,$a_2a_8$取得最大值$64$。
方法三:(基本量思想):设数列$\{ a_n\}$的公差为$d(d \geq 0)$,
因为$S_9 = 9a_1 + \frac{9 × 8d}{2} = 9a_1 + 36d = 72$,
所以$a_1 + 4d = 8$,即$a_1 = 8 - 4d$,
所以$a_2a_8 = (a_1 + d)(a_1 + 7d) = (8 - 4d + d)(8 - 4d + 7d) = (8 - 3d)(8 + 3d) = 64 - 9d^2$,
当$d = 0$时,$a_2a_8$取得最大值$64$。
所以$a_2 + a_8 = 2a_5 = 16$,
因为$16 = a_2 + a_8 \geq 2\sqrt{a_2a_8}$,即$\frac{1}{2}(\sqrt{a_2a_8})^2 + 2\sqrt{a_2a_8} - 16 \leq 0$,
所以$\frac{1}{2}(\sqrt{a_2a_8} + 6)(\sqrt{a_2a_8} - 2) \leq 0$,所以$-6 \leq \sqrt{a_2a_8} \leq 2$,
又因为$\sqrt{a_2a_8} > 0$,所以$0 < \sqrt{a_2a_8} \leq 2$,当且仅当$a_2 = a_8 = 8$时取等号。
所以$a_2a_8 \leq 64$,当且仅当$a_2 = a_8 = 8$时取等号。
方法二:因为$S_9 = \frac{(a_1 + a_9) × 9}{2} = \frac{2a_5 × 9}{2} = 9a_5 = 72$,
所以$a_5 = 8$,所以$a_2 + a_8 = 2a_5 = 16$,
则$a_2a_8 = a_2(16 - a_2) = -a_2^2 + 16a_2 = -(a_2 - 8)^2 + 64$,
故当$a_2 = 8$时,$a_2a_8$取得最大值$64$。
方法三:(基本量思想):设数列$\{ a_n\}$的公差为$d(d \geq 0)$,
因为$S_9 = 9a_1 + \frac{9 × 8d}{2} = 9a_1 + 36d = 72$,
所以$a_1 + 4d = 8$,即$a_1 = 8 - 4d$,
所以$a_2a_8 = (a_1 + d)(a_1 + 7d) = (8 - 4d + d)(8 - 4d + 7d) = (8 - 3d)(8 + 3d) = 64 - 9d^2$,
当$d = 0$时,$a_2a_8$取得最大值$64$。
13. 若 $ \sin 2\alpha = \frac{\sqrt{5}}{5} $,$ \sin (\beta - \alpha) = \frac{\sqrt{10}}{10} $,且 $ \alpha \in \left[ \frac{\pi}{4}, \frac{\pi}{2} \right] $,$ \beta \in \left[ \pi, \frac{3}{2}\pi \right] $,则 $ \alpha + \beta = $
$\frac{7\pi}{4}$
.
答案:
13.$\frac{7\pi}{4}$ 因$\alpha \in [\frac{\pi}{4}, \frac{\pi}{2}]$,所以$2\alpha \in [\frac{\pi}{2}, \pi]$,又$\sin 2\alpha = \frac{\sqrt{5}}{5} > 0$,所以$2\alpha \in (\frac{\pi}{2}, \pi)$。
根据$\sin^2 2\alpha + \cos^2 2\alpha = 1$,
得$\cos 2\alpha = -\sqrt{1 - \sin^2 2\alpha} = -\sqrt{1 - (\frac{\sqrt{5}}{5})^2} = -\frac{2\sqrt{5}}{5}$,同时也能确定$\alpha \in (\frac{\pi}{4}, \frac{\pi}{2})$。
因为$\sin(\beta - \alpha) = \frac{\sqrt{10}}{10}$,$\beta \in [\pi, \frac{3\pi}{2}]$,$\alpha \in (\frac{\pi}{4}, \frac{\pi}{2})$,
所以$\beta - \alpha \in (\frac{\pi}{2}, \frac{5\pi}{4})$。
$\cos(\beta - \alpha) = -\sqrt{1 - \sin^2(\beta - \alpha)} = -\sqrt{1 - (\frac{\sqrt{10}}{10})^2} = -\frac{3\sqrt{10}}{10}$,
所以$\cos(\alpha + \beta) = \cos[(\beta - \alpha) + 2\alpha] = \cos(\beta - \alpha)\cos 2\alpha - \sin(\beta - \alpha)\sin 2\alpha$
$= (-\frac{3\sqrt{10}}{10}) × (-\frac{2\sqrt{5}}{5}) - \frac{\sqrt{10}}{10} × \frac{\sqrt{5}}{5} = \frac{3\sqrt{10} × 2\sqrt{5}}{10 × 5} - \frac{\sqrt{10} × \sqrt{5}}{10 × 5} = \frac{6\sqrt{50} - \sqrt{50}}{50} = \frac{5\sqrt{50}}{50} = \frac{\sqrt{2}}{2}$,
因为$\alpha \in (\frac{\pi}{4}, \frac{\pi}{2})$,$\beta \in [\pi, \frac{3\pi}{2}]$,
所以$\alpha + \beta \in (\frac{5\pi}{4}, 2\pi)$。
在这个区间内,$\cos(\alpha + \beta) = \frac{\sqrt{2}}{2}$时,
$\alpha + \beta = \frac{7\pi}{4}$。
根据$\sin^2 2\alpha + \cos^2 2\alpha = 1$,
得$\cos 2\alpha = -\sqrt{1 - \sin^2 2\alpha} = -\sqrt{1 - (\frac{\sqrt{5}}{5})^2} = -\frac{2\sqrt{5}}{5}$,同时也能确定$\alpha \in (\frac{\pi}{4}, \frac{\pi}{2})$。
因为$\sin(\beta - \alpha) = \frac{\sqrt{10}}{10}$,$\beta \in [\pi, \frac{3\pi}{2}]$,$\alpha \in (\frac{\pi}{4}, \frac{\pi}{2})$,
所以$\beta - \alpha \in (\frac{\pi}{2}, \frac{5\pi}{4})$。
$\cos(\beta - \alpha) = -\sqrt{1 - \sin^2(\beta - \alpha)} = -\sqrt{1 - (\frac{\sqrt{10}}{10})^2} = -\frac{3\sqrt{10}}{10}$,
所以$\cos(\alpha + \beta) = \cos[(\beta - \alpha) + 2\alpha] = \cos(\beta - \alpha)\cos 2\alpha - \sin(\beta - \alpha)\sin 2\alpha$
$= (-\frac{3\sqrt{10}}{10}) × (-\frac{2\sqrt{5}}{5}) - \frac{\sqrt{10}}{10} × \frac{\sqrt{5}}{5} = \frac{3\sqrt{10} × 2\sqrt{5}}{10 × 5} - \frac{\sqrt{10} × \sqrt{5}}{10 × 5} = \frac{6\sqrt{50} - \sqrt{50}}{50} = \frac{5\sqrt{50}}{50} = \frac{\sqrt{2}}{2}$,
因为$\alpha \in (\frac{\pi}{4}, \frac{\pi}{2})$,$\beta \in [\pi, \frac{3\pi}{2}]$,
所以$\alpha + \beta \in (\frac{5\pi}{4}, 2\pi)$。
在这个区间内,$\cos(\alpha + \beta) = \frac{\sqrt{2}}{2}$时,
$\alpha + \beta = \frac{7\pi}{4}$。
查看更多完整答案,请扫码查看


