2026年一本密卷高考数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年一本密卷高考数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
17. 如图,母线长为 3 的圆台形状的实木筒(壁厚忽略不计)两底面的半径分别为 1,2,在该实木筒内放入一个等高的正三棱台物体,则该正三棱台物体的体积的最大值为

$\frac{7\sqrt{6}}{2}$
.
答案:
17. $\frac{7\sqrt{6}}{2}$ 当正三棱台的两底面正三角形为圆台的两底面圆的内接正三角形时,该正三棱台的体积取得最大值。
因为圆台的母线长为3,两底面圆的半径分别为1与2,
所以圆台的高$h = \sqrt{3^2 - (2 - 1)^2} = 2\sqrt{2}$。
设正三棱台两底面正三角形的边长分别为$a$,$b(a < b)$,
由正弦定理可得$\frac{a}{\sin 60°} = 2× 1$,$\frac{b}{\sin 60°} = 2× 2$,
解得$a = \sqrt{3}$,$b = 2\sqrt{3}$,
故该正三棱台物体的体积的最大值为
$V = \frac{2\sqrt{2}}{3}(\frac{\sqrt{3}}{4}a^2×\frac{\sqrt{3}}{4}ab + \frac{\sqrt{3}}{4}b^2) = \frac{2\sqrt{2}}{3}×[\frac{\sqrt{3}}{4}×(\sqrt{3})^2 + \frac{\sqrt{3}}{4}×\sqrt{3}× 2\sqrt{3} + \frac{\sqrt{3}}{4}×(2\sqrt{3})^2] = \frac{7\sqrt{6}}{2}$。
因为圆台的母线长为3,两底面圆的半径分别为1与2,
所以圆台的高$h = \sqrt{3^2 - (2 - 1)^2} = 2\sqrt{2}$。
设正三棱台两底面正三角形的边长分别为$a$,$b(a < b)$,
由正弦定理可得$\frac{a}{\sin 60°} = 2× 1$,$\frac{b}{\sin 60°} = 2× 2$,
解得$a = \sqrt{3}$,$b = 2\sqrt{3}$,
故该正三棱台物体的体积的最大值为
$V = \frac{2\sqrt{2}}{3}(\frac{\sqrt{3}}{4}a^2×\frac{\sqrt{3}}{4}ab + \frac{\sqrt{3}}{4}b^2) = \frac{2\sqrt{2}}{3}×[\frac{\sqrt{3}}{4}×(\sqrt{3})^2 + \frac{\sqrt{3}}{4}×\sqrt{3}× 2\sqrt{3} + \frac{\sqrt{3}}{4}×(2\sqrt{3})^2] = \frac{7\sqrt{6}}{2}$。
18. 已知三棱锥 $ A - BCD $ 中,$ AB = AD $,$ BC = CD = BD = 2 $,二面角 $ A - BD - C $ 为直二面角,三棱锥 $ A - BCD $ 的各个顶点都在球 $ M $ 上,球 $ M $ 的表面积为 $ \frac{112\pi}{9} $,则三棱锥 $ A - BCD $ 的体积为
$\sqrt{3}$
.
答案:
18. $\sqrt{3}$ 如图,取$BD$的中点$O$,连接$AO$,$CO$,由$AB = AD$,$BC = CD = BD = 2$,得$AO\perp BD$,$CO\perp BD$,
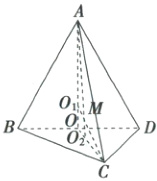
所以$\angle AOC$为二面角$A - BD - C$的平面角,
因为二面角$A - BD - C$为直二面角,所以$\angle AOC = 90°$,
即$AO\perp OC$,又$BD\cap OC = O$,
所以$AO\perp$平面$BCD$,
所以$AO$即三棱锥$A - BCD$的高。
设$\triangle ABD$与$\triangle BCD$的外接圆的圆心分别为$O_1$,$O_2$,则$O_1$,$O_2$分别在$AO$,$CO$上,连接$MO_1$,$MO_2$,$AM$,$CM$。
由$BC = CD = BD = 2$可得$CO = \sqrt{3}$,$CO_2 = \frac{2\sqrt{3}}{3}$,
$OO_2 = \frac{\sqrt{3}}{3}$。
设球$M$的半径为$R$,则$4\pi R^2 = \frac{112\pi}{9}$,
得$R^2 = \frac{28}{9}$。
所以$AO = AO_1 + MO_2 = \sqrt{R^2 - MO_1^2} + \sqrt{R^2 - CO_2^2}$
$ = \sqrt{\frac{28}{9} - (\frac{\sqrt{3}}{3})^2} + \sqrt{\frac{28}{9} - (\frac{2\sqrt{3}}{3})^2} = 3$,
所以$V_{A - BCD} = \frac{1}{3}S_{\triangle BCD}× AO = \frac{1}{3}×\frac{\sqrt{3}}{4}× 2^2× 3 = \sqrt{3}$。
18. $\sqrt{3}$ 如图,取$BD$的中点$O$,连接$AO$,$CO$,由$AB = AD$,$BC = CD = BD = 2$,得$AO\perp BD$,$CO\perp BD$,

所以$\angle AOC$为二面角$A - BD - C$的平面角,
因为二面角$A - BD - C$为直二面角,所以$\angle AOC = 90°$,
即$AO\perp OC$,又$BD\cap OC = O$,
所以$AO\perp$平面$BCD$,
所以$AO$即三棱锥$A - BCD$的高。
设$\triangle ABD$与$\triangle BCD$的外接圆的圆心分别为$O_1$,$O_2$,则$O_1$,$O_2$分别在$AO$,$CO$上,连接$MO_1$,$MO_2$,$AM$,$CM$。
由$BC = CD = BD = 2$可得$CO = \sqrt{3}$,$CO_2 = \frac{2\sqrt{3}}{3}$,
$OO_2 = \frac{\sqrt{3}}{3}$。
设球$M$的半径为$R$,则$4\pi R^2 = \frac{112\pi}{9}$,
得$R^2 = \frac{28}{9}$。
所以$AO = AO_1 + MO_2 = \sqrt{R^2 - MO_1^2} + \sqrt{R^2 - CO_2^2}$
$ = \sqrt{\frac{28}{9} - (\frac{\sqrt{3}}{3})^2} + \sqrt{\frac{28}{9} - (\frac{2\sqrt{3}}{3})^2} = 3$,
所以$V_{A - BCD} = \frac{1}{3}S_{\triangle BCD}× AO = \frac{1}{3}×\frac{\sqrt{3}}{4}× 2^2× 3 = \sqrt{3}$。
19. 已知曲线 $ C_{1}:x^{2}+y^{2} = 4y(x\geqslant 0) $,曲线 $ C_{2}:x^{2}+y^{2}-2y - 8 = 0(x < 0,y > 0) $,直线 $ l:y = \sqrt{3}x + m $,若直线 $ l $ 与曲线 $ C_{1} $,$ C_{2} $ 都有公共点,则实数 $ m $ 的取值范围为
$(-\infty, -2)\cup(7, +\infty)$
.
答案:
19. $(-\infty, -2)\cup(7, +\infty)$ 曲线$C_1$是以$(0, 2)$为圆心,2为半径的圆在$y$轴上及$y$轴右侧的部分,曲线$C_2$是以$(0, 1)$为圆心,3为半径的圆在$x$轴上方、$y$轴左侧的部分,如图。因为直线$l: y = \sqrt{3}x + m$的倾斜角为$60°$,所以当直线$l$与曲线$C_1$相切于点$Q$时,设直线$l$与$y$轴交于点$M(0, m_1)$,连接$C_1Q$,则$\vert C_1M\vert = 2\vert C_1Q\vert = 4$,则$m_1 = -2$,当直线$l$与曲线$C_2$相切于点$T$时,设直线$l$与$y$轴交于点$P(0, m_2)$,连接$C_2T$,则$\vert C_2P\vert = 2\vert C_2T\vert = 6$,则$m_2 = 7$。
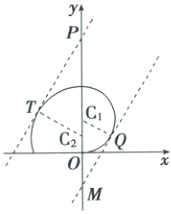
结合图形可知,若直线$l$与曲线$C_1$,$C_2$都没有公共点,则实数$m$的取值范围为$(-\infty, -2)\cup(7, +\infty)$。
19. $(-\infty, -2)\cup(7, +\infty)$ 曲线$C_1$是以$(0, 2)$为圆心,2为半径的圆在$y$轴上及$y$轴右侧的部分,曲线$C_2$是以$(0, 1)$为圆心,3为半径的圆在$x$轴上方、$y$轴左侧的部分,如图。因为直线$l: y = \sqrt{3}x + m$的倾斜角为$60°$,所以当直线$l$与曲线$C_1$相切于点$Q$时,设直线$l$与$y$轴交于点$M(0, m_1)$,连接$C_1Q$,则$\vert C_1M\vert = 2\vert C_1Q\vert = 4$,则$m_1 = -2$,当直线$l$与曲线$C_2$相切于点$T$时,设直线$l$与$y$轴交于点$P(0, m_2)$,连接$C_2T$,则$\vert C_2P\vert = 2\vert C_2T\vert = 6$,则$m_2 = 7$。

结合图形可知,若直线$l$与曲线$C_1$,$C_2$都没有公共点,则实数$m$的取值范围为$(-\infty, -2)\cup(7, +\infty)$。
20. 已知直线 $ l $ 与圆 $ O:x^{2}+y^{2} = 20 $ 相交于 $ A $,$ B $ 两点,以线段 $ AB $ 为直径的圆经过定点 $ P(2,0) $,则 $ AB $ 的中点 $ Q $ 的轨迹方程为
$(x - 1)^2 + y^2 = 9$
.
答案:
20. $(x - 1)^2 + y^2 = 9$ 设$Q(x, y)$,连接$OQ$,$PQ$,因为弦$AB$的中点为$Q$,$O$为圆心,圆$O$的半径为$2\sqrt{5}$,
所以$\vert OQ\vert^2 = 20 - \vert AQ\vert^2$,
又以线段$AB$为直径的圆经过定点$P(2, 0)$,
则$\vert PQ\vert = \vert AQ\vert$,所以$\vert OQ\vert^2 + \vert PQ\vert^2 = 20$。
方法一:即$x^2 + y^2 + (x - 2)^2 + y^2 = 20$,整理得$(x - 1)^2 + y^2 = 9$。
方法二:取线段$OP$的中点$M(1, 0)$,连接$MQ$,则由中线长公式可得$4\vert MQ\vert^2 + \vert OP\vert^2 = 2(\vert OQ\vert^2 + \vert PQ\vert^2) = 40$,所以$\vert MQ\vert^2 = 9$,$\vert MQ\vert = 3$,所以$Q$的轨迹是以$M(1, 0)$为圆心、3为半径的圆。故点$Q$的轨迹方程为$(x - 1)^2 + y^2 = 9$。
所以$\vert OQ\vert^2 = 20 - \vert AQ\vert^2$,
又以线段$AB$为直径的圆经过定点$P(2, 0)$,
则$\vert PQ\vert = \vert AQ\vert$,所以$\vert OQ\vert^2 + \vert PQ\vert^2 = 20$。
方法一:即$x^2 + y^2 + (x - 2)^2 + y^2 = 20$,整理得$(x - 1)^2 + y^2 = 9$。
方法二:取线段$OP$的中点$M(1, 0)$,连接$MQ$,则由中线长公式可得$4\vert MQ\vert^2 + \vert OP\vert^2 = 2(\vert OQ\vert^2 + \vert PQ\vert^2) = 40$,所以$\vert MQ\vert^2 = 9$,$\vert MQ\vert = 3$,所以$Q$的轨迹是以$M(1, 0)$为圆心、3为半径的圆。故点$Q$的轨迹方程为$(x - 1)^2 + y^2 = 9$。
21. 某数学兴趣小组根据电影《哪吒 2》上映 20 天内,上映天数 $ x $ 与累计票房 $ y $(单位:亿元)的散点图(下图),选择应用模型 $ y = b\sqrt{x}+a $ 来拟合 $ y $ 与 $ x $ 的关系.
(1) 求 $ y $ 关于 $ x $ 的回归方程,并依据此方程预测电影上映 25 天后的累计票房;(结果保留一位小数)
(2) 某数据统计机构分析发现电影《哪吒 2》的观众中,年龄在 20~29 岁的占比 28%,在 30~39 岁的占比 41%,40 岁以上的占比 21%.某记者从电影院观看《哪吒 2》的人群中随机抽取 3 位观众采访,求抽到年龄在 20 岁以下的观众人数 $ X $ 的分布列与期望.
附:在 $ \hat{y} = \hat{b}x+\hat{a} $ 中 $ \hat{b} = \frac{\sum_{i = 1}^{n}x_{i}y_{i}-n\overline{x}\overline{y}}{\sum_{i = 1}^{n}x_{i}^{2}-n\overline{x}^{2}} $,$ \hat{a} = \overline{y}-\hat{b}\overline{x} $.
参考数据:$ \sqrt{x_{i}} = t_{i} $,$ \overline{t}\approx 3.08 $,$ \overline{y}\approx 66.5 $,$ \sum_{i = 1}^{20}t_{i}^{2}\approx 210 $,$ \sum_{i = 1}^{20}x_{i}^{2}\approx 2870 $,$ \sum_{i = 1}^{20}t_{i}y_{i}\approx 4816.35 $,$ \sum_{i = 1}^{20}x_{i}y_{i}\approx 18114.22 $.

(1) 求 $ y $ 关于 $ x $ 的回归方程,并依据此方程预测电影上映 25 天后的累计票房;(结果保留一位小数)
(2) 某数据统计机构分析发现电影《哪吒 2》的观众中,年龄在 20~29 岁的占比 28%,在 30~39 岁的占比 41%,40 岁以上的占比 21%.某记者从电影院观看《哪吒 2》的人群中随机抽取 3 位观众采访,求抽到年龄在 20 岁以下的观众人数 $ X $ 的分布列与期望.
附:在 $ \hat{y} = \hat{b}x+\hat{a} $ 中 $ \hat{b} = \frac{\sum_{i = 1}^{n}x_{i}y_{i}-n\overline{x}\overline{y}}{\sum_{i = 1}^{n}x_{i}^{2}-n\overline{x}^{2}} $,$ \hat{a} = \overline{y}-\hat{b}\overline{x} $.
参考数据:$ \sqrt{x_{i}} = t_{i} $,$ \overline{t}\approx 3.08 $,$ \overline{y}\approx 66.5 $,$ \sum_{i = 1}^{20}t_{i}^{2}\approx 210 $,$ \sum_{i = 1}^{20}x_{i}^{2}\approx 2870 $,$ \sum_{i = 1}^{20}t_{i}y_{i}\approx 4816.35 $,$ \sum_{i = 1}^{20}x_{i}y_{i}\approx 18114.22 $.

答案:
21. 解:
(1)由题意知$\hat{b} = \frac{\sum_{i = 1}^{20}t_i y_i - n\bar{t}\bar{y}}{\sum_{i = 1}^{20}t_i^2 - n\bar{t}^2} \approx \frac{4816.35 - 20× 3.08× 66.5}{210 - 20× 3.08^2} = \frac{719.95}{20.272} \approx 35.5$,$\hat{a} = \bar{y} - \hat{b}\bar{t} \approx -42.8$,所以$\hat{y} = 35.5\sqrt{x} - 42.8$。
当$x = 25$时,$\hat{y} = 35.5× 5 - 42.8 = 134.7$,
故预测电影上映25天后的累计票房为134.7亿元。
(2)由题意知年龄在20岁以下的观众占比10%,则$X\sim B(3, 0.1)$,
所以$P(X = 0) = C_3^0(0.1)^0(0.9)^3 = 0.729$,
$P(X = 1) = C_3^1(0.1)^1(0.9)^2 = 0.243$,
$P(X = 2) = C_3^2(0.1)^2(0.9)^1 = 0.027$,
$P(X = 3) = C_3^3(0.1)^3(0.9)^0 = 0.001$。
$X$的分布列为
| $X$ | 0 | 1 | 2 | 3 |
| --- | --- | --- | --- | --- |
| $P$ | 0.729 | 0.243 | 0.027 | 0.001 |
所以$E(X) = 0 + 0.243 + 2× 0.027 + 3× 0.001 = 0.3$。
(1)由题意知$\hat{b} = \frac{\sum_{i = 1}^{20}t_i y_i - n\bar{t}\bar{y}}{\sum_{i = 1}^{20}t_i^2 - n\bar{t}^2} \approx \frac{4816.35 - 20× 3.08× 66.5}{210 - 20× 3.08^2} = \frac{719.95}{20.272} \approx 35.5$,$\hat{a} = \bar{y} - \hat{b}\bar{t} \approx -42.8$,所以$\hat{y} = 35.5\sqrt{x} - 42.8$。
当$x = 25$时,$\hat{y} = 35.5× 5 - 42.8 = 134.7$,
故预测电影上映25天后的累计票房为134.7亿元。
(2)由题意知年龄在20岁以下的观众占比10%,则$X\sim B(3, 0.1)$,
所以$P(X = 0) = C_3^0(0.1)^0(0.9)^3 = 0.729$,
$P(X = 1) = C_3^1(0.1)^1(0.9)^2 = 0.243$,
$P(X = 2) = C_3^2(0.1)^2(0.9)^1 = 0.027$,
$P(X = 3) = C_3^3(0.1)^3(0.9)^0 = 0.001$。
$X$的分布列为
| $X$ | 0 | 1 | 2 | 3 |
| --- | --- | --- | --- | --- |
| $P$ | 0.729 | 0.243 | 0.027 | 0.001 |
所以$E(X) = 0 + 0.243 + 2× 0.027 + 3× 0.001 = 0.3$。
查看更多完整答案,请扫码查看


