《2026年一本密卷高考数学》

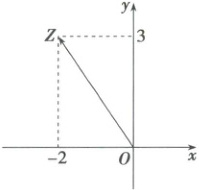
1. 如图,向量$\overrightarrow{OZ}$对应的复数是$z$,则$z· \overline{z}$的值为


A.6
B.$\sqrt{6}$
C.13
D.$\sqrt{13}$

答案： 1.C 由题意，向量$\overrightarrow{OZ}$对应的复数是$z = - 2 + 3i$，则$z · \overline{z} = |z|^{2} = ( - 2)^{2} + 3^{2} = 13$。故选C。

2. 若集合$M=\{x\mid -3\lt x\lt 1\},N=\{x\mid \frac{1}{x + 2}\geqslant 1\}$,则$M\cap N$等于

A.$\{x\mid -1\lt x\lt 2\}$
B.$\{x\mid -2\lt x\leqslant -1\}$
C.$\{x\mid -3\lt x\lt -2\}$
D.$\{x\mid -1\leqslant x\lt 1\}$

答案： 2.B 因为$\frac{1}{x + 2} \geqslant 1 \Leftrightarrow \frac{1}{x + 2} - 1 \geqslant 0 \Leftrightarrow \frac{- x - 1}{x + 2} \geqslant 0 \Leftrightarrow \begin{cases} (x + 2)(x + 1) \leqslant 0 \\ x + 2 \neq 0 \end{cases}$，所以$- 2 ＜ x \leqslant - 1$，所以$N = \left\{ x\left| \frac{1}{x + 2} \geqslant 1 \right. \right\} = \{ x| - 2 ＜ x \leqslant - 1\}$，又$M = \{ x| - 3 ＜ x ＜ 1\}$，所以$M \cap N = \{ x| - 2 ＜ x \leqslant - 1\}$。故选B。

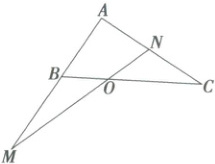
3. 如图,在$\triangle ABC$中,点$O$是线段$BC$上靠近点$B$的三等分点,过点$O$的直线分别交直线$AB$、$AC$于点$M$、$N$.设$\overrightarrow{AB}=m\overrightarrow{AM},\overrightarrow{AC}=n\overrightarrow{AN}$,则$2m + n$的值为(C)


A.1
B.2
C.3
D.4

答案：
3.C 连接$AO$，因为点$O$是线段$BC$上靠近点$B$的三等分点，则$\overrightarrow{CO} = 2\overrightarrow{OB}$，即$\overrightarrow{AO} - \overrightarrow{AC} = 2(\overrightarrow{AB} - \overrightarrow{AO})$，
所以，$\overrightarrow{AO} = \frac{2}{3}\overrightarrow{AB} + \frac{1}{3}\overrightarrow{AC}$，又因为$\overrightarrow{AB} = m\overrightarrow{AM},\overrightarrow{AC} = n\overrightarrow{AN}$，则$\overrightarrow{AO} = \frac{2}{3}m\overrightarrow{AM} + \frac{1}{3}n\overrightarrow{AN}$，因为$M,N,O$三点共线，设$\overrightarrow{MO} = k\overrightarrow{MN}$，则$\overrightarrow{AO} - \overrightarrow{AM} = k(\overrightarrow{AN} - \overrightarrow{AM})$，所以，$\overrightarrow{AO} = (1 - k)\overrightarrow{AM} + k\overrightarrow{AN}$，且$\overrightarrow{AM},\overrightarrow{AN}$不共线，
所以$\frac{2}{3}m = 1 - k,\frac{1}{3}n = k$，故$\frac{2}{3}m + \frac{1}{3}n = 1 - k + k = 1$，因此$2m + n = 3$。
故选C。

4. 已知双曲线$C:\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}} = 1(a\gt 0,b\gt 0)$的左、右焦点分别为$F_{1},F_{2}$,若以$F_{1}F_{2}$为直径的圆与以点$P(\sqrt{2},\frac{1}{2})$为圆心、$\frac{3}{2}$为半径的圆相切于点$Q$,且点$Q$在$C$上,则$C$的离心率为

A.$\frac{\sqrt{6}}{2}$
B.$\sqrt{6}$
C.$\sqrt{3}$
D.$\frac{3}{2}$

答案：
4.A 由两圆的圆心分别为$O(0,0),P(\sqrt{2},\frac{1}{2})$，且圆$P$的半径为$\frac{3}{2}$，$|OP| = \sqrt{2 + \frac{1}{4}} = \frac{3}{2}$，可得点$P$在以$F_1F_2$为直径的圆内，且两圆内切，所以点$P$为$OQ$的中点，所以$Q(2\sqrt{2},1),|OQ| = \sqrt{8 + 1} = 3$，所以圆$O$的半径为$3$，即$|OF_1| = 3$，所以$\begin{cases} a^{2} + b^{2} = 9 \\ \frac{8}{a^{2}} - \frac{1}{b^{2}} = 1 \end{cases}$，解得$a = \sqrt{6},b = \sqrt{3}$，所以C的离心率为$\frac{3}{\sqrt{6}} = \frac{\sqrt{6}}{2}$。
故选A。

5. 已知$a\gt 2,8^{a}+15^{a}=17^{b}$,则

A.$a\gt b\gt 2$
B.$a\gt 2\gt b$
C.$b\gt a\gt 2$
D.$b\gt 2$,但$a$和$b$的大小关系无法确定

答案： 5.A 由于$a ＞ 2$，所以$17^{b} = 8^{a} + 15^{a} ＞ 8^{2} + 15^{2} = 17^{2}$，因此$b ＞ 2$，又因为$17^{b - a} = (\frac{8}{17})^{a} + (\frac{15}{17})^{a} ＜ (\frac{8}{17})^{2} + (\frac{15}{17})^{2} = 1$，即$b - a ＜ 0$，故$2 ＜ b ＜ a$。故选A。

6. 对于独立性检验,下列说法中错误的是

A.$\chi^{2}$的值越大,说明两事件相关程度越大
B.$\chi^{2}$的值越小,说明两事件相关程度越小
C.$\chi^{2}\leqslant 3.841$时,则在犯错误的概率不超过$0.05$的前提下认为事件$A$与$B$有关
D.$\chi^{2}\gt 3.841$时,则可以大概率认为事件$A$与$B$有关

答案： 6.C 对于$A,B$，因观测值$\chi^{2} = \frac{n(ad - bc)^{2}}{(a + b)(c + d)(a + c)(b + d)}$，$\chi^{2}$的值越大，$|ad - bc|$越大，事件$A$与事件$B$关系越强；反之，事件$A$与事件$B$关系越弱，故$A,B$项均正确；对于$C,D$，因只有$P(\chi^{2} \geqslant 3.841) \approx 0.05$时，说明在犯错误的概率不超过$0.05$的前提下认为事件$A$与$B$有关，而$\chi^{2} \leqslant 3.841$，故$C$错误；$D$正确。故选C。