《2026年一本密卷高考数学》

16.（15分）设数列$\{a_{n}\}$满足$a_{1}=3$，$\frac{a_{n + 1}}{n}=\frac{a_{n}}{n + 1}+\frac{1}{n(n + 1)}$。
（1）证明：$\{na_{n}\}$为等差数列；
（2）设$f(x)=a_{1}x + a_{2}x^{2}+·s + a_{m}x^{m}$，求$f'(-2)$。

答案： （1）证明：由题意，$n\in N^*$，
在数列$\{a_n\}$中，$a_1 = 3$，$\frac{a_{n + 1}}{n}=\frac{a_n}{n + 1}+\frac{1}{n(n + 1)}$，
$\therefore(n + 1)a_{n + 1}=na_n + 1$，即$(n + 1)a_{n + 1}-na_n = 1$，
$\therefore\{na_n\}$是以$a_1 = 3$为首项，1为公差的等差数列。
（2）由题意及（1）得，$n\in N^*$，
在数列$\{na_n\}$中，首项为3，公差为1，
$\therefore na_n=3 + 1×(n - 1)$，即$a_n=1+\frac{2}{n}$，
在$f(x)=a_1x + a_2x^2+·s+a_mx^m$中，
$f(x)=3x + 2x^2+·s+(1+\frac{2}{m})x^m$，
$f'(x)=3 + 4x+·s+(m + 2)x^{m - 1}$，
$\begin{cases}f'(x)=3 + 4x+·s+(m + 2)x^{m - 1}\\xf'(x)=3x + 4x^2+·s+(m + 2)x^m\end{cases}$
当$x\neq1$且$x\neq0$时，
$\therefore(1 - x)f'(x)=3 + x + x^2+·s+x^{m - 1}-(m + 2)x^m=\frac{3(1 - x^m)}{1 - x}-\frac{x(1 - x^{m - 1})}{1 - x}-(m + 2)x^m$，
$\therefore f'(x)=\frac{3}{1 - x}+\frac{x(1 - x^{m - 1})}{(1 - x)^2}-\frac{(m + 2)x^m}{1 - x}$
$\therefore f'(-2)=\frac{3}{1 - (-2)}+\frac{-2[1 - (-2)^{m - 1}]}{[1 - (-2)]^2}-\frac{(m + 2)(-2)^m}{1 - (-2)}$
$=1+\frac{(-2)[1 - (-2)^{m - 1}]}{9}-\frac{(m + 2)(-2)^m}{3}$
$=1-\frac{2}{9}-\frac{-2[1 - (-2)^{m - 1}]}{9}-\frac{(3m + 7)(-2)^m}{9}$
$=\frac{7}{9}-\frac{(3m + 7)(-2)^m}{9}$。

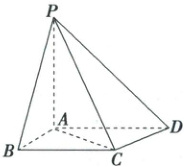
17.（15分）如图所示的四棱锥$P - ABCD$中，$PA\perp$平面$ABCD$，$BC// AD$，$AB\perp AD$。
（1）证明：平面$PAB\perp$平面$PAD$；
（2）$PA = AB=\sqrt{2}$，$AD = 1+\sqrt{3}$，$BC = 2$，$P$，$B$，$C$，$D$在同一个球面上，设该球面的球心为$O$。
（ⅰ）证明：$O$在平面$ABCD$上；
（ⅱ）求直线$AC$与直线$PO$所成角的余弦值。

答案：
（1）证明：在四棱锥$P - ABCD$中，$PA\perp$平面$ABCD$，$AB\perp AD$，
$AB\subset$平面$ABCD$，$AD\subset$平面$ABCD$，
所以$AP\perp AB$，$AP\perp AD$，
因为$AP\subset$平面$PAD$，$AD\subset$平面$PAD$，$AP\cap AD = A$，
所以$AB\perp$平面$PAD$，
因为$AB\subset$平面$PAB$，
所以平面$PAB\perp$平面$PAD$。
（2）（ⅰ）证明：方法一：在四棱锥$P - ABCD$中，$AP\perp AB$，$AP\perp AD$，$AB\perp AD$，$BC// AD$，$PA = AB=\sqrt{2}$，$AD = 1+\sqrt{3}$，
建立空间直角坐标系如下图所示，

所以$A(0,0,0)$，$B(\sqrt{2},0,0)$，$C(\sqrt{2},2,0)$，$D(0,1+\sqrt{3},0)$，$P(0,0,\sqrt{2})$，
若$P$，$B$，$C$，$D$在同一个球面上，则$|OP| = |OB| = |OC| = |OD|$。
在平面$xAy$中，

所以$A(0,0)$，$B(\sqrt{2},0)$，$C(\sqrt{2},2)$，$D(0,1+\sqrt{3})$，所以线段$CD$中点坐标$F(\frac{\sqrt{2}}{2},\frac{\sqrt{3}+3}{2})$。
直线$CD$的斜率：$k_1=\frac{1+\sqrt{3}-2}{0 - \sqrt{2}}=-\frac{\sqrt{3}-1}{\sqrt{2}}$，
直线$CD$的垂直平分线$EF$斜率：$k_2=\frac{\sqrt{2}}{\sqrt{3}-1}=\frac{\sqrt{6}+\sqrt{2}}{2}$，
所以直线$CD$的方程：$y-\frac{\sqrt{3}+3}{2}=\frac{\sqrt{6}+\sqrt{2}}{2}(x - \frac{\sqrt{2}}{2})$，
即$y=\frac{\sqrt{6}+\sqrt{2}}{2}(x - \frac{\sqrt{2}}{2})+\frac{\sqrt{3}+3}{2}$，
当$y = 1$时，$1=\frac{\sqrt{6}+\sqrt{2}}{2}(x_0 - \frac{\sqrt{2}}{2})+\frac{\sqrt{3}+3}{2}$，
解得：$x_0 = 0$，
所以$O(0,1)$。
在立体几何中，$O(0,1,0)$，
$\begin{cases}|OP|=\sqrt{0^2 + 1^2+(0 - \sqrt{2})^2}\\|OB|=\sqrt{(0 - \sqrt{2})^2+1^2+0^2}\\|OC|=\sqrt{(0 - \sqrt{2})^2+(1 - 2)^2+0^2}\\|OD|=\sqrt{0^2+(1 - 1 - \sqrt{3})^2+0^2}\end{cases}$
解得：$|OP| = |OB| = |OC| = |OD|=\sqrt{3}$，
所以点$O$在平面$ABCD$上。
方法二：因为$P$，$B$，$C$，$D$在同一个球面上，
所以球心到四个点的距离相等。
在$\triangle BCD$中，到三角形三点距离相等的点是该三角形的外心，
作出$BC$和$CD$的垂直平分线，如下图所示，

由几何知识得，
$OE = AB=\sqrt{2}$，$BE = CE = AO_1 = GO_1=\frac{1}{2}BC = 1$，$O_1D = AD - AO_1=\sqrt{3}$，
$BO_1 = CO_1=\sqrt{1^2+(\sqrt{2})^2}=\sqrt{3}$，
所以$O_1D = BO_1 = CO_1$，
所以点$O_1$是$\triangle BCD$的外心。
在$Rt\triangle AO_1P$中，$AP\perp AD$，$AP=\sqrt{2}$，
由勾股定理得，

$PO_1=\sqrt{AP^2 + AO_1^2}=\sqrt{(\sqrt{2})^2+1^2}=\sqrt{3}$，
所以$PO_1 = BO_1 = CO_1 = O_1D=\sqrt{3}$，
所以点$O_1$即为点$P$，$B$，$C$，$D$所在球的球心$O$，此时点$O$在线段$AD$上，$AD\subset$平面$ABCD$，
所以点$O$在平面$ABCD$上。
（ⅱ）方法一：由题意，（1）（2）（ⅱ）及图得，

设直线$AC$与直线$PO$所成角为$\theta$，
所以$\cos\theta=\frac{|\overrightarrow{AC}·\overrightarrow{PO}|}{|\overrightarrow{AC}||\overrightarrow{PO}|}$
$=\frac{| \sqrt{2}×0 + 2×1+0|}{\sqrt{(\sqrt{2})^2+2^2+0^2}×\sqrt{0^2+1^2+(-\sqrt{2})^2}}=\frac{\sqrt{2}}{3}$。
方法二：由几何知识得，$PO=\sqrt{3}$，
$AB\perp AD$，$BC// AD$，
所以$AB\perp BC$，
在$Rt\triangle ABC$中，$AB=\sqrt{2}$，$BC = 2$，由勾股定理得，
$AC=\sqrt{AB^2 + BC^2}=\sqrt{(\sqrt{2})^2+2^2}=\sqrt{6}$。
过点$O$作$AC$的平行线，交$BC$的延长线于$C_1$，连接$AC_1$，$PC_1$，

则$OC_1 = AC=\sqrt{6}$，直线$AC$与直线$PO$所成角即为$\triangle POC_1$中$\angle POC_1$或其补角。
因为$PA\perp$平面$ABCD$，$AC_1\subset$平面$ABCD$，$PA\cap AC_1 = A$，
所以$PA\perp AC_1$，
在$Rt\triangle ABC_1$中，$AB=\sqrt{2}$，$BC_1 = BC + CC_1 = 2 + 1 = 3$，由勾股定理得，
$AC_1=\sqrt{AB^2 + BC_1^2}=\sqrt{(\sqrt{2})^2+3^2}=\sqrt{11}$，
在$Rt\triangle APC_1$中，$PA=\sqrt{2}$，由勾股定理得，
$PC_1=\sqrt{PA^2 + AC_1^2}=\sqrt{(\sqrt{2})^2+(\sqrt{11})^2}=\sqrt{13}$，
在$\triangle POC_1$中，由余弦定理得，
$PC_1^2 = PO^2 + OC_1^2-2PO· OC_1\cos\angle POC_1$，
即$(\sqrt{13})^2=(\sqrt{3})^2+(\sqrt{6})^2-2\sqrt{3}×\sqrt{6}\cos\angle POC_1$，
解得：$\cos\angle POC_1=-\frac{\sqrt{2}}{3}$。
所以直线$AC$与直线$PO$所成角的余弦值为$|\cos\angle POC_1|=\frac{\sqrt{2}}{3}$。