《2026年一本密卷高考数学》

23. 近年来，有着中国特色的潮流文化开始大热，人们称之为“国潮”，构成“国潮”的元素十分丰富.“非遗”作为中国传统文化的重要组成部分，越来越受到年轻人的追捧，成为了新“国潮”.某旅游景区为吸引更多游客前来，推出了打铁花、舞龙舞狮等非遗展演活动，下表统计了该景区推出非遗展演活动后第 $ x $ 个月的营业额 $ y $（单位：千万元）.

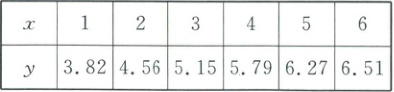
(1) 通过回归分析，可以利用模型 $ \hat{y} = b\sqrt{x}+a $ 对 $ y $ 与 $ x $ 的关系进行拟合，利用表格数据，求出 $ y $ 关于 $ x $ 的回归方程；（结果保留两位小数）
(2) 为了庆祝“春节”申遗成功，该景区特在 2025 年春节期间推出了抽奖活动，规则如下：游客从含有 5 张舞龙图案与 $ k(k\geqslant 5) $ 张舞狮图案的卡池中一次性抽取 2 张卡片，记录所抽取卡片的图案，然后将卡片放回卡池中，再重复抽取 2 次，若这 3 次中恰有 1 次抽取的 2 张卡片图案不相同，则游客中奖.当 $ k $ 为多少时，游客中奖概率最高？
附：对于一组具有线性相关关系的数据 $ (u_{1},v_{1}) $，$ (u_{2},v_{2}) $，$ ·s $，$ (u_{n},v_{n}) $，其对应经验回归直线 $ \hat{v} = \hat{\beta}u+\hat{\alpha} $ 的斜率和截距的最小二乘估计分别为 $ \hat{\beta} = \frac{\sum_{i = 1}^{n}(u_{i}-\overline{u})(v_{i}-\overline{v})}{\sum_{i = 1}^{n}(u_{i}-\overline{u})^{2}} $，$ \hat{\alpha} = \overline{v}-\hat{\beta}\overline{u} $.
参考数据：$ t_{i} = \sqrt{x_{i}}(i = 1,2,·s,6) $，$ \overline{t}\approx 1.81 $，$ \sum_{i = 1}^{6}y_{i} = 32.1 $，$ \sum_{i = 1}^{6}x_{i}y_{i} = 121.96 $，$ \sum_{i = 1}^{6}t_{i}y_{i}\approx 60.74 $.

答案： 23. 解：
(1)由题意知$\bar{y} = \frac{32.1}{6} = 5.35$，$\sum_{i = 1}^6 t_i^2 = \sum_{i = 1}^6 x_i = 1 + 2 + 3 + 4 + 5 + 6 = 21$，
则$\hat{b} = \frac{\sum_{i = 1}^6 (t_i - \bar{t})(y_i - \bar{y})}{\sum_{i = 1}^6 (t_i - \bar{t})^2}$
$ = \frac{\sum_{i = 1}^6 t_i y_i - 6\bar{t}\bar{y}}{\sum_{i = 1}^6 t_i^2 - 6\bar{t}^2}$
$\approx \frac{60.74 - 6× 1.81× 5.35}{21 - 6× 1.81^2} \approx 1.96$，
所以$\hat{a} = \bar{y} - \hat{b}\bar{t} \approx 5.35 - 1.96× 1.81 \approx 1.80$，
所以$y$关于$x$的回归方程为$\hat{y} = 1.96\sqrt{x} + 1.80$。
(2)设游客一次性从卡池中抽取2张卡片，图案不相同的概率为$p$，游客中奖的概率为$P$，
由题意知$p = \frac{C_5^1· C_k^1}{C_{5 + k}^2} = \frac{5k}{\frac{(5 + k)!}{2!·(3 + k)!}} = \frac{10k}{(5 + k)(4 + k)}$，
则$P = C_3^1 p(1 - p)^2 = 3p^3 - 6p^2 + 3p$。
设$f(x) = \frac{10x}{(5 + x)(4 + x)}(x\geq 5)$，
则$f(x) = \frac{10}{x + \frac{20}{x} + 9}$，
易知$y = x + \frac{20}{x} + 9$在$(5, +\infty)$上单调递增，
则$f(x)$在$(5, +\infty)$上单调递减，
所以$f(x) \leq \frac{10}{5 + \frac{20}{5} + 9} = \frac{5}{9}$，
即$0 ＜ p \leq \frac{5}{9}$。
设$g(x) = 3x^3 - 6x^2 + 3x(0 ＜ x \leq \frac{5}{9})$，
则$g'(x) = 9x^2 - 12x + 3 = 3(3x - 1)(x - 1)$，
所以$g(x)$在$(0, \frac{1}{3})$上单调递增，在$(\frac{1}{3}, \frac{5}{9}]$上单调递减，
所以当$p = \frac{10k}{(5 + k)(4 + k)} = \frac{1}{3}$时，$P$取最大值，
此时$k = 1$（舍去）或$k = 20$。
所以当$k$为20时，游客中奖概率最高。