《2026年一本密卷高考数学》

7. 若函数$f(x)$的定义域内存在$x_{1},x_{2}(x_{1}\neq x_{2})$,使得$\frac{f(x_{1})+f(x_{2})}{2}=1$成立,则称$f(x)$为“完整函数”.已知$f(x)=\frac{\sqrt{3}}{2}\sin(\omega x-\frac{\pi}{6})-\frac{1}{2}\cos(\omega x+\frac{5\pi}{6})(\omega\gt 0)$是$[\frac{3\pi}{2},\frac{5\pi}{2}]$上的“完整函数”,则$\omega$的取值范围为

A.$[\frac{13}{5},3]\cup [\frac{17}{5},4)$
B.$[\frac{13}{5},3]\cup [\frac{17}{5},+\infty)$
C.$[\frac{13}{5},+\infty)$
D.$[\frac{13}{5},3]\cup [4,+\infty)$

答案： 7.B 由题意得$f(x) = \frac{\sqrt{3}}{2}\sin(\omega x - \frac{\pi}{6}) - \frac{1}{2}\cos(\omega x + \frac{5\pi}{6}) = \frac{\sqrt{3}}{2}\sin(\omega x - \frac{\pi}{6}) + \frac{1}{2}\cos(\omega x - \frac{\pi}{6}) = \sin\omega x$，因为$\frac{f(x_{1}) + f(x_{2})}{2} = 1$，所以$f(x_{1}) + f(x_{2}) = 2$，故$f(x)$在$[\frac{3\pi}{2},\frac{5\pi}{2}]$上有两个最大值点，令$\omega x = t$，则函数$y = \sin t$在区间$[\frac{3\omega\pi}{2},\frac{5\omega\pi}{2}]$上至少存在两个最大值点，则$\frac{2\pi}{\omega} \leqslant \pi$，解得$\omega \geqslant 2$。
当$2T = \frac{4\pi}{\omega} \leqslant \pi$，即$\omega \geqslant 4$时，显然符合题意。
当$2 \leqslant \omega ＜ 4$时，因为$\frac{3\pi}{2} \leqslant x \leqslant \frac{5\pi}{2}$，所以$\frac{3\omega\pi}{2} \leqslant \omega x \leqslant \frac{5\omega\pi}{2}$，因为$2 \leqslant \omega ＜ 4$，所以$3\pi \leqslant \frac{3\omega\pi}{2} ＜ 6\pi,5\pi \leqslant \frac{5\omega\pi}{2} ＜ 10\pi$，分以下两种情况讨论：
①当$\frac{3\omega\pi}{2} \leqslant \frac{9\pi}{2}$，即$\omega \leqslant 3$时，$\frac{5\omega\pi}{2} \geqslant \frac{13\pi}{2}$，即$\omega \geqslant \frac{13}{5}$，所以$\frac{13}{5} \leqslant \omega \leqslant 3$。
②当$\frac{9\pi}{2} ＜ \frac{3\omega\pi}{2} ＜ 6\pi$，即$3 ＜ \omega ＜ 4$时，$\frac{5\omega\pi}{2} \geqslant \frac{17\pi}{2}$，即$\omega \geqslant \frac{17}{5}$，所以$\frac{17}{5} \leqslant \omega ＜ 4$。
综上，$\omega$的取值范围为$[\frac{13}{5},3] \cup [\frac{17}{5}, + \infty)$，故B正确。故选B。

8. 已知正实数$x,y$满足$\frac{x}{2}+2y - 2=\ln x+\ln y$,则$y^{x}=$

A.2
B.$\sqrt{2}$
C.$\frac{1}{4}$
D.$\frac{\sqrt{2}}{2}$

答案： 8.C 由题设可得$\ln(xy) = \frac{x}{2} + 2y - 2 \geqslant 2\sqrt{xy} - 2$（当且仅当$x = 4y$时取等号），即$\ln(xy) \geqslant 2\sqrt{xy} - 2$，由于$x,y$均为正实数，即$\ln\sqrt{xy} \geqslant \sqrt{xy} - 1$，设$m(x) = \ln x - x + 1$，则当$x ＞ 1$时，$m^{\prime}(x) = \frac{1}{x} - 1 ＜ 0$，$m(x)$在$(1, + \infty)$单调递减，当$0 ＜ x ＜ 1$时，$m^{\prime}(x) ＞ 0$，$m(x)$在$(0,1)$单调递增，故当$m(x) \leqslant m(1) = 0$，故$\ln x \leqslant x - 1$，当且仅当$x = 1$时取等号，因此$\ln\sqrt{xy} \leqslant \sqrt{xy} - 1$，故$\ln\sqrt{xy} = \sqrt{xy} - 1$，则$\begin{cases} x = 4y \\ \sqrt{xy} = 1 \end{cases}$，解得$\begin{cases} x = 2 \\ y = \frac{1}{2} \end{cases}$，所以$y^{x} = \frac{1}{4}$。
故选C。

9. 下列关于概率统计的知识,其中说法正确的是

A.数据$-3,-1,3,7,8,9,11,15$的第$25$百分位数是$1$
B.若一组样本数据$(x_{i},y_{i})(i = 1,2,·s,n)$的对应样本点都在直线$y=-\frac{1}{3}x + 1$上,则这组样本数据的相关系数为$-\frac{1}{3}$
C.已知随机变量$X\sim B(n,p)$,若$E(X)=36,D(X)=9$,则$n = 48$
D.某班有$50$名同学,一次考试后的数学成绩服从正态分布$N(100,10^{2})$,则理论上说在$90\sim 100$分的人数约为$17$人.(参考数据:$P(\mu-\sigma\leqslant X\leqslant\mu+\sigma)\approx 0.6827,P(\mu - 2\sigma\leqslant X\leqslant\mu+2\sigma)\approx 0.9545,P(\mu - 3\sigma\leqslant X\leqslant\mu+3\sigma)\approx 0.9973$

答案： 9.ACD 对于选项A，$8$个数据从小到大排列，由于$8 × 25\% = 2$，所以第$25$百分位数应该是第二个与第三个的平均数$\frac{- 1 + 3}{2} = 1$，故A正确；对于选项B，因为样本点都在直线$y = - \frac{1}{3}x + 1$上，说明是负相关且线性相关性很强，所以相关系数为$- 1$，故B错误。对于选项C，因为$X \sim B(n,p),E(X) = 36$，$D(X) = 9$，所以$\begin{cases} np = 36 \\ np(1 - p) = 9 \end{cases}$，解得$p = \frac{3}{4},n = 48$，故C正确；对于选项D，由$P(90 \leqslant x \leqslant 100) = \frac{1}{2}P(\mu - \sigma \leqslant x \leqslant \mu + \sigma) = 0.34135$，可得在$90 \sim 100$分的人数是：$50 × 0.34135 \approx 17$，故D正确。故选ACD。

10. 已知函数$f(x)=\ln\frac{x}{2 - x}+ax + b(x - 1)^{3}$,则

A.函数$f(x)$的定义域为$(0,2)$
B.当$a = 0,b = 0$时,函数$f(x)$在定义域上单调递增
C.曲线$y = f(x)$是中心对称图形
D.若$b = 0$,且$f'(x)\geqslant 0,a$的最小值是$0$

答案： 10.ABC 对于A，由函数解析式可得$\frac{x}{2 - x} ＞ 0$，解得$0 ＜ x ＜ 2$，因此函数$f(x)$的定义域为$(0,2)$，显然A正确；对于B，当$a = 0,b = 0$时，$f(x) = \ln\frac{x}{2 - x} = \ln x - \ln(2 - x)$，易知函数$y = \ln x$单调递增，$y = \ln(2 - x)$单调递减，所以函数$f(x)$在定义域上单调递增，B正确；对于C，令$g(x) = \ln\frac{x}{2 - x}$，$g(2 - x) = \ln\frac{2 - x}{x}$，$g(x) + g(2 - x) = 0$，因此$g(x)$的图象关于点$(1,0)$中心对称，易知$f(x) = g(x) + a(x - 1) + a + b(x - 1)^{2}$满足$f(x) + f(2 - x) = 2a$，可得$f(x)$的图象关于点$(1,a)$中心对称，可得C正确；对于D，$b = 0$时，$f(x) = \ln\frac{x}{2 - x} + ax$，其中$x \in (0,2)$，则$f^{\prime}(x) = \frac{1}{x} + \frac{1}{2 - x} + a = \frac{2}{x(2 - x)} + a$，$x \in (0,2)$，因为$x(2 - x) \leqslant (\frac{2 - x + x}{2})^{2} = 1$，当且仅当$x = 1$时等号成立，故$f^{\prime}(x)_{\min} = 2 + a$，而$f^{\prime}(x) \geqslant 0$成立，故$a + 2 \geqslant 0$，即$a \geqslant - 2$，所以$a$的最小值为$- 2$，即D错误。
故选：ABC。

11. 数学中有许多形状优美的曲线,曲线$E:3x^{2}+3y^{2}-2|xy| = 8$就是其中之一、下列说法正确的是

A.曲线$E$有$4$条对称轴
B.曲线$E$内有$9$个整点(横、纵坐标均为整数的点)
C.若$M(x,y)$是曲线$E$上的任意一点,则$3y - x$的最大值为$5$
D.设直线$y = kx(k\gt 0)$与曲线$E$交于$A,B$两点,则$|AB|$的最大值为$4$

答案：
11.ABD 对于A，点$(x,y)$是曲线$E$上任意点，显然$(x, - y),( - x,y),(y,x),( - y, - x)$都满足曲线$E$的方程，因此曲线$E$关于$x$轴、$y$轴、直线$y = x$、直线$y = - x$都对称，A正确；对于B，由$3|x|^{2} - 2|y||x| + 3|y|^{2} - 8 = 0$，得$\Delta = 4|y|^{2} - 12(3|y|^{2} - 8) \geqslant 0$，解得$|y| \leqslant \sqrt{3}$，同理$|x| \leqslant \sqrt{3}$，因此曲线$E$在两组平行直线$x = \pm \sqrt{3},y = \pm \sqrt{3}$所围成的正方形及内部，而点$( \pm 1, \pm 1),(0, \pm 1),( \pm 1,0),(0,0)$中，任意一点坐标都使$3x^{2} + 3y^{2} - 2|xy| - 8 ＜ 0$，因此曲线$E$内有$9$个整点，B正确；

对于C，由曲线$E$的对称性知，当$M(x,y)$位于第二象限时，$3y - x$取得最大值，此时方程为$3x^{2} + 3y^{2} + 2xy = 8$，令$t = 3y - x$，将$x = 3y - t$代入$3x^{2} + 3y^{2} + 2xy = 8$，得$36y^{2} - a20ty + 3t^{2} - 8 = 0$，故$\Delta^{\prime} = 400t^{2} - 144(3t^{2} - 8) \geqslant 0$，解得$|t| \leqslant 6$，因此$3y - x$的最大值为$6$，C错误；对于D，由$\begin{cases} y = kx \\ 3x^{2} + 3y^{2} - 2|xy| = 8 \end{cases}$消去$y$得$x^{2} = \frac{8}{3k^{2} - 2k + 3}$，解得$x = \pm \frac{2\sqrt{2}}{\sqrt{3k^{2} - 2k + 3}}$，则$|AB| = \sqrt{k^{2} + 1} · \frac{4\sqrt{2}}{\sqrt{3k^{2} - 2k + 3}} = \frac{4\sqrt{2}}{\sqrt{3 - \frac{2k}{k^{2} + 1}}}$，当且仅当$k = 1$时取等号，D正确。
故选ABD。

12. 某池塘中水生植物的覆盖水塘面积$x$(单位:$dm^{2}$)与水生植物的株数$y$(单位:株)之间的相关关系,收集了$4$组数据,用模型$y = ce^{bx}(c\gt 0)$去拟合$x$与$y$的关系,设$z=\ln y,x$与$z$的数据如表格所示:

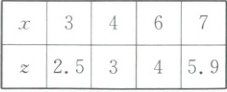
得到$x$与$z$的经验回归方程$\hat{z}=0.7x+\hat{a}$,则$c=$$e^{0.35}$.

答案： 12.$e^{0.35}$ 由已知可得，$\overline{x} = \frac{3 + 4 + 6 + 7}{4} = 5$，$\overline{z} = \frac{2.5 + 3 + 4 + 5.9}{4} = 3.85$，所以$3.85 = 0.7 × 5 + \hat{a}$，解得$\hat{a} = 0.35$，所以$\hat{z} = 0.7x + 0.35$。由$z = \ln y$，得$\ln y = 0.7x + 0.35$，所以$y = e^{0.7x + 0.35} = e^{0.35} · e^{0.7x}$，所以$c = e^{0.35}$。

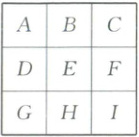
13. 如图,有一个触屏感应灯,该灯共有$9$个灯区,每个灯区都处于“点亮”或“熄灭”状态,触摸按其中一个灯区,将导致该灯区及相邻(上、下或左、右相邻)的灯区改变状态.假设起初所有灯区均处于“点亮”状态,若从中随机先后按下两个不同灯区,则$B,G$灯区最终仍处于“点亮”状态的概率为$\frac{5}{18}$.

答案： 13.$\frac{5}{18}$ 从$9$个灯区中随机先后按下两个灯区，共有$A_{9}^{2} = 72$种按法。与$B$相邻的灯区为$A,C,E$；与$G$相邻的灯区为$D,H$，故将$9$个灯区分为三类：第一类$F,I$灯区，第二类$A,B,C,E$灯区，第三类$D,G,H$灯区。若要使得$B,G$灯区最终仍处于“点亮”状态，则需在同类灯区中随机先后按两个不同灯区。①若先后按下的是$F,I$两个灯区，则$B,G$灯区最终仍处于“点亮”状态，共有$A_{2}^{2} = 2$种按法；②若先后按下的是$A,B,C,E$灯区中的两个，则$B,G$灯区最终仍处于“点亮”状态，共有$A_{4}^{2} = 12$种按法；③若先后按下的是$D,G,H$灯区中的两个，则$B,G$灯区最终仍处于“点亮”状态，共有$A_{3}^{2} = 6$种按法。故$B,G$灯区最终仍处于“点亮”状态的概率为$\frac{2 + 12 + 6}{72} = \frac{5}{18}$。