2026年一本密卷高考数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年一本密卷高考数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. (多选)北京时间 2024 年 7 月 27 日,中国双人组合在巴黎奥运会中夺得射击混合团体 10 米气步枪冠军,这是 2024 巴黎奥运会产生的首枚金牌,也是中国代表团在本届奥运会获得的首枚金牌.两人在决赛中的 14 次射击环数如图所示,则(
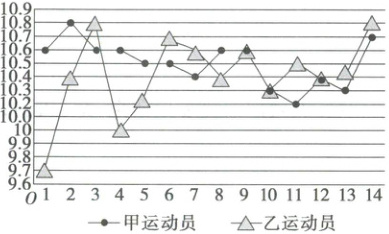
A.乙运动员的平均射击环数约为 10.4
B.甲运动员射击环数的第 75 百分位数为 10.6
C.乙运动员射击环数的方差小于甲运动员射击环数的方差
D.甲运动员射击环数的极差小于乙运动员射击环数的极差
ABD
)
A.乙运动员的平均射击环数约为 10.4
B.甲运动员射击环数的第 75 百分位数为 10.6
C.乙运动员射击环数的方差小于甲运动员射击环数的方差
D.甲运动员射击环数的极差小于乙运动员射击环数的极差
答案:
1. ABD 对于A,乙运动员的平均射击环数为$\frac{1}{14}$×(9.7+10.4+10.8+10+10.2+10.7+10.6+10.4+10.6+10.3+10.5+10.4+10.4+10.8)≈10.4,故A正确。对于B,将甲运动员的射击环数从小到大排列为10.2,10.3,10.3,10.4,10.4,10.5,10.5,10.6,10.6,10.6,10.6,10.6,10.7,10.8,14×0.75 = 10.5,则甲运动员射击环数的第75百分位数是从小到大排列的第11个数,即10.6,故B正确。对于C,乙运动员的射击环数更分散,故方差更大,故C错误。对于D,甲运动员的射击环数极差为10.8−10.2 = 0.6,乙运动员的射击环数极差为10.8−9.7 = 1.1,故D正确。故选ABD。
2. 已知双曲线 $ C:\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}} = 1(a > 0,b > 0) $ 的右焦点为 $ F $,$ M $,$ N $ 为直线 $ y = \frac{b}{a}x $ 上关于坐标原点对称的两点,$ A $ 为双曲线的右顶点,若 $ \overrightarrow{FM}·\overrightarrow{FN} = 0 $,且 $ \sin\angle MAN = \frac{\sqrt{6}}{3} $,则双曲线 $ C $ 的离心率为(
A.$ \sqrt{3} $
B.$ \frac{\sqrt{6}}{2} $
C.$ \sqrt{15} $
D.$ \sqrt{33} $
A
)A.$ \sqrt{3} $
B.$ \frac{\sqrt{6}}{2} $
C.$ \sqrt{15} $
D.$ \sqrt{33} $
答案:
2. A 因为$\overrightarrow{FM}·\overrightarrow{FN} = 0$,所以$FM\perp FN$,又$M, N$为直线$y = \frac{b}{a}x$上关于坐标原点对称的两点,$F(c, 0)$,所以$\vert OM\vert = \vert ON\vert = \vert OF\vert = c$($O$为坐标原点)。
设$M(x_0, \frac{b}{a}x_0)$,
则$\sqrt{x_0^2 + (\frac{b}{a}x_0)^2} = c$,
可得$x_0^2(1 + \frac{b^2}{a^2}) = c^2$,
而$1 + \frac{b^2}{a^2} = \frac{c^2}{a^2}$,
所以$x_0^2 = a^2$,则$x_0 = a$或$x_0 = -a$。
不妨取$M(a, b)$,$N(-a, -b)$。
因为$A(a, 0)$,所以$\overrightarrow{AM} = (0, b)$,$\overrightarrow{AN} = (-2a, -b)$。
$\vert\overrightarrow{AM}\vert = b$,$\vert\overrightarrow{AN}\vert = \sqrt{(-2a)^2 + (-b)^2} = \sqrt{4a^2 + b^2}$,
$\overrightarrow{AM}·\overrightarrow{AN} = 0×(-2a) + b×(-b) = -b^2$。
因为$\sin\angle MAN = \frac{\sqrt{6}}{3}$,
所以$\cos\angle MAN = \pm\sqrt{1 - (\frac{\sqrt{6}}{3})^2} = \pm\frac{\sqrt{3}}{3}$。
根据向量的夹角公式得$\cos\angle MAN = \frac{\overrightarrow{AM}·\overrightarrow{AN}}{\vert\overrightarrow{AM}\vert\vert\overrightarrow{AN}\vert}$
$ = \frac{-b^2}{b\sqrt{4a^2 + b^2}} = -\frac{\sqrt{3}}{3}$。
两边平方可得$\frac{b^4}{b^2(4a^2 + b^2)} = \frac{1}{3}$,化简得$3b^2 = 4a^2 + b^2$,即$b^2 = 2a^2$。
又$c^2 = a^2 + b^2$,把$b^2 = 2a^2$代入可得$c^2 = 3a^2$。
故双曲线的离心率$e = \frac{c}{a} = \sqrt{3}$。
故选A。
设$M(x_0, \frac{b}{a}x_0)$,
则$\sqrt{x_0^2 + (\frac{b}{a}x_0)^2} = c$,
可得$x_0^2(1 + \frac{b^2}{a^2}) = c^2$,
而$1 + \frac{b^2}{a^2} = \frac{c^2}{a^2}$,
所以$x_0^2 = a^2$,则$x_0 = a$或$x_0 = -a$。
不妨取$M(a, b)$,$N(-a, -b)$。
因为$A(a, 0)$,所以$\overrightarrow{AM} = (0, b)$,$\overrightarrow{AN} = (-2a, -b)$。
$\vert\overrightarrow{AM}\vert = b$,$\vert\overrightarrow{AN}\vert = \sqrt{(-2a)^2 + (-b)^2} = \sqrt{4a^2 + b^2}$,
$\overrightarrow{AM}·\overrightarrow{AN} = 0×(-2a) + b×(-b) = -b^2$。
因为$\sin\angle MAN = \frac{\sqrt{6}}{3}$,
所以$\cos\angle MAN = \pm\sqrt{1 - (\frac{\sqrt{6}}{3})^2} = \pm\frac{\sqrt{3}}{3}$。
根据向量的夹角公式得$\cos\angle MAN = \frac{\overrightarrow{AM}·\overrightarrow{AN}}{\vert\overrightarrow{AM}\vert\vert\overrightarrow{AN}\vert}$
$ = \frac{-b^2}{b\sqrt{4a^2 + b^2}} = -\frac{\sqrt{3}}{3}$。
两边平方可得$\frac{b^4}{b^2(4a^2 + b^2)} = \frac{1}{3}$,化简得$3b^2 = 4a^2 + b^2$,即$b^2 = 2a^2$。
又$c^2 = a^2 + b^2$,把$b^2 = 2a^2$代入可得$c^2 = 3a^2$。
故双曲线的离心率$e = \frac{c}{a} = \sqrt{3}$。
故选A。
查看更多完整答案,请扫码查看


