《2026年一本密卷高考数学》

3. 已知 $ \sin\alpha-\cos(\alpha-\frac{\pi}{6}) = \frac{\sqrt{5}}{3} $，则 $ \cos(2\alpha-\frac{2\pi}{3}) $ 的值为(B)

A.$ \frac{4}{9} $
B.$ -\frac{1}{9} $
C.$ \frac{4}{5} $
D.$ -\frac{1}{5} $

答案： 3. B $\sin\alpha - \cos(\alpha - \frac{\pi}{6}) = \frac{\sqrt{5}}{3}$，即$\sin\alpha - \cos\alpha\cos\frac{\pi}{6} - \sin\alpha\sin\frac{\pi}{6} = \frac{1}{2}\sin\alpha - \frac{\sqrt{3}}{2}\cos\alpha = \sin(\alpha - \frac{\pi}{3}) = \frac{\sqrt{5}}{3}$，
所以$\cos(2\alpha - \frac{2\pi}{3}) = 1 - 2\sin^2(\alpha - \frac{\pi}{3}) = 1 - \frac{10}{9} = -\frac{1}{9}$。故选B。

4. (多选)已知函数 $ f(x) = \sqrt{3}\sin2x+\sin^{4}x-\cos^{4}x,x\in\mathbf{R} $，则(ABD)

A.$ f(\frac{\pi}{6}+x)+f(-x) = 0 $
B.$ |f(x)|\leqslant f(\frac{\pi}{3}) $
C.$ f(x) $ 在 $ [-\frac{\pi}{4},\frac{\pi}{4}] $ 上单调递增
D.若 $ f(x+\varphi) $ 为偶函数，则 $ |\varphi| $ 的最小值为 $ \frac{\pi}{6} $

答案： 4. ABD $f(x) = \sqrt{3}\sin2x + \sin^4x - \cos^4x = \sqrt{3}\sin2x + (\sin^2x + \cos^2x)(\sin^2x - \cos^2x) = \sqrt{3}\sin2x - \cos2x = 2\sin(2x - \frac{\pi}{6})$。若$f(\frac{\pi}{6} + x) + f(-x) = 0$，则函数$f(x)$的图象关于$(\frac{\pi}{12}, 0)$对称，$f(\frac{\pi}{12}) = 2\sin(2×\frac{\pi}{12} - \frac{\pi}{6}) = 0$，满足对称条件，A正确；因为$f(\frac{\pi}{3}) = 2\sin(2×\frac{\pi}{3} - \frac{\pi}{6}) = 2$，即函数$f(x)$在$x = \frac{\pi}{3}$处取得最大值，所以$\vert f(x)\vert \leq f(\frac{\pi}{3})$恒成立，B正确；由$x\in[-\frac{\pi}{4}, \frac{\pi}{4}]$，得$2x - \frac{\pi}{6}\in[-\frac{2\pi}{3}, \frac{\pi}{3}]$，所以函数$f(x)$在$[-\frac{\pi}{4}, \frac{\pi}{4}]$上不单调，C错误；$f(x + \varphi) = 2\sin[2(x + \varphi) - \frac{\pi}{6}] = 2\sin(2x + 2\varphi - \frac{\pi}{6})$，若其为偶函数，则$2\varphi - \frac{\pi}{6} = k\pi + \frac{\pi}{2}(k\in Z)$，则$\varphi = \frac{k\pi}{2} + \frac{\pi}{3}(k\in Z)$，所以$\vert\varphi\vert_{min} = \frac{\pi}{6}$，D正确。故选ABD。

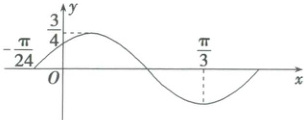
5. 信息在传递中多数是以波的形式进行传递的，因而必然会存在干扰信号波(干扰信号波的解析式形如 $ y = A\sin(\omega x+\varphi)(A ＞ 0,\omega ＞ 0,|\varphi| ＜ \frac{\pi}{2}) $).某种“信号净化器”可产生解析式形如 $ y = A_{0}\sin(\omega_{0}x+\varphi_{0}) $ 的波，只需要调整参数 $ (A_{0},\omega_{0},\varphi_{0}) $，就可以产生与干扰波波峰相同，方向相反的波来“抵消”干扰.右图是某个信号的部分图象，想要通过“信号净化器”过滤得到标准的正弦波(即仅含有标准正弦函数图象)，可以将净化器的参数调整为(B)


A.$ A_{0} = \frac{3}{4},\omega_{0} = 4,\varphi_{0} = \frac{\pi}{6} $
B.$ A_{0} = -\frac{3}{4},\omega_{0} = 4,\varphi_{0} = \frac{\pi}{6} $
C.$ A_{0} = 1,\omega_{0} = 1,\varphi_{0} = 0 $
D.$ A_{0} = -1,\omega_{0} = 1,\varphi_{0} = 0 $

答案： 5. B 由题可知干扰波对应的函数解析式为$f(x) = A\sin(\omega x + \varphi)(A ＞ 0, \omega ＞ 0, \vert\varphi\vert ＜ \frac{\pi}{2})$。
由题图得$\frac{\pi}{3} - (-\frac{\pi}{24}) = \frac{3}{4}T$（$T$为干扰波的最小正周期），
可得$T = \frac{\pi}{2}$，所以$\omega = \frac{2\pi}{T} = 4$。
因为函数$f(x)$的最大值为$\frac{3}{4}$，
所以$A = \frac{3}{4}$，
将$(\frac{\pi}{3}, -\frac{3}{4})$代入$f(x) = \frac{3}{4}\sin(4x + \varphi)$，
得$\varphi = \frac{\pi}{6} + 2k\pi(k\in Z)$，
又$\vert\varphi\vert ＜ \frac{\pi}{2}$，
所以$\varphi = \frac{\pi}{6}$，
所以$f(x) = \frac{3}{4}\sin(4x + \frac{\pi}{6})$。
欲消除此干扰波，需要选择波峰相同，方向相反的波，
所以$A_0 = -\frac{3}{4}$，$\omega_0 = 4$，$\varphi_0 = \frac{\pi}{6}$。故选B。