2026年一本密卷高考数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年一本密卷高考数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
9.(2025·天津市滨海新区三模)已知复数 $ z $ 满足 $ z(1+2\mathrm{i})=|3-4\mathrm{i}| $(其中 $ \mathrm{i} $ 为虚数单位),则复数 $ z $ 为
1-2i
。
答案:
9.$1-2i$ 因为复数$z$满足$z(1+2i)=\vert3-4i\vert$,所以$z=\frac{5}{1+2i}=\frac{5(1-2i)}{(1+2i)(1-2i)}=1-2i$.
10.(2025·山东威海市三模)已知向量 $ \boldsymbol{a},\boldsymbol{b} $ 满足 $ |\boldsymbol{a}|=4 $,$ |\boldsymbol{b}|=1 $,$ (\boldsymbol{a}-2\boldsymbol{b}) \perp \boldsymbol{b} $,则 $ \boldsymbol{a} $ 与 $ \boldsymbol{b} $ 的夹角为
$\frac{\pi}{3}$
。
答案:
10.$\frac{\pi}{3}$ 因为$(a-2b)\perp b$,所以$(a-2b)· b=0$,得$a· b=2b^{2}=2$,因为$\cos\langle a,b\rangle=\frac{a· b}{\vert a\vert\vert b\vert}=\frac{2}{4×1}=\frac{1}{2}$,所以$a$与$b$的夹角为$\frac{\pi}{3}$.
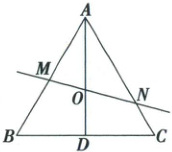
11.(13 分)(2025·天津市滨海新区三模)已知正 $ \triangle ABC $ 的边长为 $ \sqrt{3} $,中心为 $ O $,过 $ O $ 的动直线 $ l $ 与边 $ AB $,$ AC $ 分别相交于点 $ M $、$ N $,$ \overrightarrow{AM}=\lambda \overrightarrow{AB} $,$ \overrightarrow{AN}=\mu \overrightarrow{AC} $,$ \overrightarrow{BD}=\overrightarrow{DC} $。
(1)若 $ \overrightarrow{AN}=2 \overrightarrow{NC}$
(2)求 $ \triangle AMN $ 与 $ \triangle ABC $ 的面积之比的最小值。

(1)若 $ \overrightarrow{AN}=2 \overrightarrow{NC}$
$-\frac{3}{4}$
$$,则 $ \overrightarrow{AD} · \overrightarrow{BN}= $ ;(2)求 $ \triangle AMN $ 与 $ \triangle ABC $ 的面积之比的最小值。
答案:
11.解:
(1)$\overrightarrow{AD}·\overrightarrow{BN}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})·(\overrightarrow{AN}-\overrightarrow{AB})=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})·(\frac{2}{3}\overrightarrow{AC}-\overrightarrow{AB})=\frac{1}{2}(-\frac{1}{3}\overrightarrow{AB}·\overrightarrow{AC}+\frac{2}{3}\overrightarrow{AC}^{2}-\overrightarrow{AB}^{2})=\frac{1}{2}×(-\frac{1}{3}×\sqrt{3}×\sqrt{3}×\frac{1}{2}+\frac{2}{3}×3-3)=-\frac{3}{4}$.
(2)因为$\overrightarrow{AO}=\frac{2}{3}×\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})=\frac{1}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$,所以$\overrightarrow{AO}=\frac{1}{3\lambda}\overrightarrow{AM}+\frac{1}{3\mu}\overrightarrow{AN}$,因为$M,O,N$三点共线,故$\frac{1}{3\lambda}+\frac{1}{3\mu}=1$,即$\frac{1}{\lambda}+\frac{1}{\mu}=3$,又因为$\frac{S_{\triangle AMN}}{S_{\triangle ABC}}=\frac{\frac{1}{2}\vert AM\vert·\vert AN\vert·\sin A}{\frac{1}{2}\vert AB\vert·\vert AC\vert\sin A}=\lambda\mu$,而$\lambda,\mu\in(0,1]$,$\frac{1}{\lambda}+\frac{1}{\mu}=3$,则$\frac{1}{\lambda}+\frac{1}{\mu}=3\geq2\sqrt{\frac{1}{\lambda}·\frac{1}{\mu}}$,即$\lambda\mu\geq\frac{4}{9}$,当且仅当$\lambda=\mu=\frac{2}{3}$时取等号,所以$\triangle AMN$与$\triangle ABC$的面积之比的最小值为$\frac{4}{9}$.
(1)$\overrightarrow{AD}·\overrightarrow{BN}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})·(\overrightarrow{AN}-\overrightarrow{AB})=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})·(\frac{2}{3}\overrightarrow{AC}-\overrightarrow{AB})=\frac{1}{2}(-\frac{1}{3}\overrightarrow{AB}·\overrightarrow{AC}+\frac{2}{3}\overrightarrow{AC}^{2}-\overrightarrow{AB}^{2})=\frac{1}{2}×(-\frac{1}{3}×\sqrt{3}×\sqrt{3}×\frac{1}{2}+\frac{2}{3}×3-3)=-\frac{3}{4}$.
(2)因为$\overrightarrow{AO}=\frac{2}{3}×\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})=\frac{1}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$,所以$\overrightarrow{AO}=\frac{1}{3\lambda}\overrightarrow{AM}+\frac{1}{3\mu}\overrightarrow{AN}$,因为$M,O,N$三点共线,故$\frac{1}{3\lambda}+\frac{1}{3\mu}=1$,即$\frac{1}{\lambda}+\frac{1}{\mu}=3$,又因为$\frac{S_{\triangle AMN}}{S_{\triangle ABC}}=\frac{\frac{1}{2}\vert AM\vert·\vert AN\vert·\sin A}{\frac{1}{2}\vert AB\vert·\vert AC\vert\sin A}=\lambda\mu$,而$\lambda,\mu\in(0,1]$,$\frac{1}{\lambda}+\frac{1}{\mu}=3$,则$\frac{1}{\lambda}+\frac{1}{\mu}=3\geq2\sqrt{\frac{1}{\lambda}·\frac{1}{\mu}}$,即$\lambda\mu\geq\frac{4}{9}$,当且仅当$\lambda=\mu=\frac{2}{3}$时取等号,所以$\triangle AMN$与$\triangle ABC$的面积之比的最小值为$\frac{4}{9}$.
12.(15 分)设两个向量 $ \boldsymbol{a},\boldsymbol{b} $ 满足 $ |\boldsymbol{a}|=1 $,$ |\boldsymbol{b}|=2 $。
(1)若 $ (2\boldsymbol{a}-\boldsymbol{b}) · (\boldsymbol{a}+\boldsymbol{b})=-3 $,求 $ \boldsymbol{a},\boldsymbol{b} $ 的夹角 $ \theta $;
(2)若 $ \boldsymbol{a},\boldsymbol{b} $ 的夹角为 $ 60^{\circ} $,向量 $ t\boldsymbol{a}+\boldsymbol{b} $ 与 $ 2\boldsymbol{a}+t\boldsymbol{b} $ 的夹角为钝角,求实数 $ t $ 的取值范围。
(1)若 $ (2\boldsymbol{a}-\boldsymbol{b}) · (\boldsymbol{a}+\boldsymbol{b})=-3 $,求 $ \boldsymbol{a},\boldsymbol{b} $ 的夹角 $ \theta $;
(2)若 $ \boldsymbol{a},\boldsymbol{b} $ 的夹角为 $ 60^{\circ} $,向量 $ t\boldsymbol{a}+\boldsymbol{b} $ 与 $ 2\boldsymbol{a}+t\boldsymbol{b} $ 的夹角为钝角,求实数 $ t $ 的取值范围。
答案:
12.解:
(1)$\because(2a-b)(a+b)=-3$,$\therefore2\vert a\vert^{2}+a· b-\vert b\vert^{2}=-3$,又$\because\vert a\vert=1,\vert b\vert=2$,$\therefore2+a· b-4=-3$即$a· b=-1$,$\therefore\cos\theta=\frac{a· b}{\vert a\vert\vert b\vert}=-\frac{1}{2}$,又$\theta\in[0,\pi]$,$\therefore\theta=\frac{2\pi}{3}$.
(2)$\because a,b$的夹角为$60°$且$\vert a\vert=1,\vert b\vert=2$,$\therefore a· b=\vert a\vert·\vert b\vert\cos60°=1×2×\frac{1}{2}=1$,$\because$向量$ta+b$与$2a+tb$的夹角为钝角,$\therefore(ta+b)(2a+tb)<0$且$ta+b$与$2a+tb$不共线,$\begin{cases}2t\vert a\vert^{2}+(t^{2}+2)a· b+t\vert b\vert^{2}<0\\t^{2}-2\neq0\end{cases}$即$\begin{cases}t^{2}+6t+2<0\\t^{2}\neq2\end{cases}$,解得:$-3-\sqrt{7}<t<-3+\sqrt{7}$且$t\neq-\sqrt{2}$实数$t$的取值范围是$\{t\mid-3-\sqrt{7}<t<-3+\sqrt{7}$且$t\neq-\sqrt{2}\}$.
(1)$\because(2a-b)(a+b)=-3$,$\therefore2\vert a\vert^{2}+a· b-\vert b\vert^{2}=-3$,又$\because\vert a\vert=1,\vert b\vert=2$,$\therefore2+a· b-4=-3$即$a· b=-1$,$\therefore\cos\theta=\frac{a· b}{\vert a\vert\vert b\vert}=-\frac{1}{2}$,又$\theta\in[0,\pi]$,$\therefore\theta=\frac{2\pi}{3}$.
(2)$\because a,b$的夹角为$60°$且$\vert a\vert=1,\vert b\vert=2$,$\therefore a· b=\vert a\vert·\vert b\vert\cos60°=1×2×\frac{1}{2}=1$,$\because$向量$ta+b$与$2a+tb$的夹角为钝角,$\therefore(ta+b)(2a+tb)<0$且$ta+b$与$2a+tb$不共线,$\begin{cases}2t\vert a\vert^{2}+(t^{2}+2)a· b+t\vert b\vert^{2}<0\\t^{2}-2\neq0\end{cases}$即$\begin{cases}t^{2}+6t+2<0\\t^{2}\neq2\end{cases}$,解得:$-3-\sqrt{7}<t<-3+\sqrt{7}$且$t\neq-\sqrt{2}$实数$t$的取值范围是$\{t\mid-3-\sqrt{7}<t<-3+\sqrt{7}$且$t\neq-\sqrt{2}\}$.
查看更多完整答案,请扫码查看


