《2026年一本密卷高考数学》

1. (2025·四川省成都市三模)函数 $ f(x)=\frac{\sin \pi x}{e^{x}+e^{-x}} $ 的部分图象大致为(D)

答案： 1.D　根据题意，函数$f(x)$定义域为$\mathbf{R}$，且$f(-x)=\frac{\sin (-\pi x)}{\mathrm{e}^{-x}+\mathrm{e}^{x}}=-\frac{\sin \pi x}{\mathrm{e}^{x}+\mathrm{e}^{-x}}=-f(x)$，所以函数$f(x)$为奇函数，图象关于原点对称，又$x\in(0,1)$时，$\pi x \in(0,\pi)$，所以$\sin \pi x＞0$，且$\mathrm{e}^{x}+\mathrm{e}^{-x}＞0$恒成立，则$f(x)＞0$，所以只有D满足.故选D.

2. (2025·江西省萍乡市三模)已知定义在 $ \mathbf{R} $ 上的函数 $ f(x) $ 满足对于任意实数 $ x,y $ 均有 $ f(xy)=yf(x) $，且 $ 2f(2)=f(1)+6 $，则 $ f(2025)= $(D)

A.675
B.1350
C.2025
D.4050

答案： 2.D　用$x$替换$y$，$y$替换$x$可得$f(xy)=yf(x)=xf(y)$，当$x\neq0$，$y\neq0$时，故可知$\frac{f(x)}{x}$是常函数，于是知当$x\neq0$时，$f(x)=cx$，其中$c$为常数，故$4c=c +6$，解得$c=2$，于是$f(2025)=2×2025=4050$.故选D.

3. (2025·河北石家庄三模)已知 $ f(x) $ 是定义在 $ \mathbf{R} $ 上的奇函数，当 $ x_{1},x_{2} \in(0,+\infty) $ 且 $ x_{1} \neq x_{2} $ 时，都有 $ \frac{x_{2} f\left(x_{1}\right)-x_{1} f\left(x_{2}\right)}{x_{1} x_{2}\left(x_{1}-x_{2}\right)}＞0 $ 成立，$ f(2025)=2025 $，则不等式 $ f(x)-x＞0 $ 的解集为(B)

A.$ (-\infty,-2025) \cup(2025,+\infty) $
B.$ (-2025,0) \cup(2025,+\infty) $
C.$ (-2025,2025) $
D.$ \left(-\frac{1}{2025}, \frac{1}{2025}\right) $

答案： 3.B　构造函数$g(x)=\frac{f(x)}{x}$，其中$x\neq0$，则$g(-x)=\frac{f(-x)}{-x}=\frac{f(x)}{x}=g(x)$，故函数$g(x)$为偶函数，当$x_1$、$x_2\in(0,+\infty)$且$x_1\neq x_2$时，都有$\frac{x_2f(x_1)-x_1f(x_2)}{x_1x_2(x_1 - x_2)}＞0$成立，不妨设$x_1＜x_2$，则$\frac{x_2f(x_1)-x_1f(x_2)}{x_1x_2}=\frac{f(x_1)}{x_1}-\frac{f(x_2)}{x_2}＜0$，即$g(x_1)＜g(x_2)$，故函数$g(x)$在$(0,+\infty)$上单调递增，在$(-\infty,0)$上单调递减，因为$f(2025)=2025$，则$g(-2025)=g(2025)=\frac{f(2025)}{2025}=1$，当$x＞0$时，由$f(x)-x＞0$得$\frac{f(x)}{x}＞1$，即$g(x)＞g(2025)$，解得$x＞2025$；当$x＜0$时，由$f(x)-x＞0$得$\frac{f(x)}{x}＜1$，即$g(x)＜g(-2025)$，解得$-2025＜x＜0$.综上所述，不等式$f(x)-x＞0$的解集为$(-2025,0)\cup(2025,+\infty)$.故选B.

4. (2025·山东威海市三模)已知函数 $ f(x)=\left\{\begin{array}{l}(1-a) x+2 a, x＜1, \\ x-\frac{1}{x}, x \geqslant 1\end{array}\right. $ 的值域为 $ \mathbf{R} $，则 $ a $ 的取值范围是(C)

A.$ (-\infty, 1) $
B.$ (-1,+\infty) $
C.$ [-1,1) $
D.$ (1,+\infty) $

答案： 4.C　因为$y=x$在$[1,+\infty)$单调递增，$y=-\frac{1}{x}$在$[1,+\infty)$单调递增，所以当$x\geqslant1$时，$f(x)=x-\frac{1}{x}$单调递增，则$f(x)\geqslant f(1)=0$，又函数$f(x)$的值域为$\mathbf{R}$，所以$x＜1$时，函数$y=(1-a)x + 2a$的值域要取到$(-\infty,0)$的所有实数，所以$1-a＞0$，当$1-a＞0$时，即$a＜1$时，函数$y=(1-a)x + 2a$单调递增，$x\to-\infty$时，$y\to-\infty$，当$x=1$时，$y=1-a + 2a=a + 1\geqslant0$，即$a\geqslant-1$，所以$-1\leqslant a＜1$，即$a$的取值范围是$[-1,1)$.故选C.

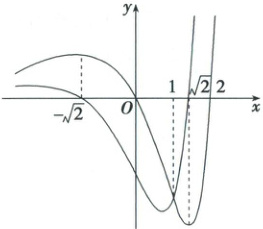
5. (2025·湖南省郴州市三模)已知函数 $ f(x) $ 与其导函数 $ f^{\prime}(x) $ 的部分图象如图所示. 设函数 $ g(x)=\frac{f(x)}{e^{x}} $，则(B)


A.$ f(0)＜f(1) $
B.$ e f(-1)＞f(0) $
C.$ g(x) $ 在 $ (1,2) $ 上单调递减
D.$ g(x) $ 在 $ x=1 $ 处取得极大值

答案：
5.B　由图可知$f(x)$、$f'(x)$的分布如图所示.

易得当$-\sqrt{2}＜x＜\sqrt{2}$时，$f'(x)＜0$，所以$f(x)$在$(-\sqrt{2},\sqrt{2})$上单调递减，则$f(0)＞f(1)$，A错误；由$g(x)=\frac{f(x)}{\mathrm{e}^{x}}$，得$g'(x)=\frac{f'(x)-f(x)}{\mathrm{e}^{x}}$.当$-\sqrt{2}＜x＜1$时，$f'(x)-f(x)＜0$，所以$g'(x)＜0$，所以$g(x)$在$(-\sqrt{2},1)$上单调递减，所以$g(-1)＞g(0)$，即$\frac{f(-1)}{\mathrm{e}^{-1}}＞\frac{f(0)}{\mathrm{e}^{0}}$，所以$\mathrm{e}f(-1)＞f(0)$，B正确；当$1＜x＜2$时，$f'(x)＞f(x)$，则$f'(x)-f(x)＞0$，所以$g'(x)＞0$，$g(x)$在$(1,2)$上单调递增，C错误；当$x=1$时，$f'(x)=f(x)$，所以$g'(x)=0$，因为$g(x)$在$(-\sqrt{2},1)$上单调递减，在$(1,2)$上单调递增，所以$g(x)$在$x=1$处取得极小值，D错误.故选B.

6. (2025·安徽省安庆市三模)已知函数 $ f(x)=e^{x}-a \ln (a x-a)+a(a＞0) $，若对于任意的 $ x＞1 $ 使得不等式 $ f(x) \geqslant 0 $ 成立，则实数 $ a $ 的取值范围是(A)

A.$ \left(0, e^{2}\right] $
B.$ \left(0, e^{e}\right] $
C.$ \left[e^{2},+\infty\right) $
D.$ \left[e^{e},+\infty\right) $

答案： 6.A　因为$a＞0$，由$ax - a＞0$可得$x＞1$，即函数$f(x)$的定义域为$(1,+\infty)$，$f(x)=\mathrm{e}^{x}-a\ln a-a\ln(x - 1)+a\geqslant0$可得$\frac{\mathrm{e}^{x}}{a}-\ln a\geqslant\ln(x - 1)-1$，即$\mathrm{e}^{x-\ln a}+x-\ln a\geqslant x - 1+\ln(x - 1)$，构造函数$g(x)=x+\ln x$，其中$x＞0$，则$g'(x)=1+\frac{1}{x}＞0$，故函数$g(x)$在$(0,+\infty)$上单调递增，所以$g(\mathrm{e}^{x-\ln a})\geqslant g(x - 1)$，可得$\mathrm{e}^{x-\ln a}\geqslant x - 1$，则$x-\ln a\geqslant\ln(x - 1)$，即$\ln a\leqslant x-\ln(x - 1)$，其中$x＞1$，令$h(x)=x-\ln(x - 1)$，其中$x＞1$，则$h'(x)=1-\frac{1}{x - 1}=\frac{x - 2}{x - 1}$，当$1＜x＜2$时，$h'(x)＜0$，此时函数$h(x)$单调递减，当$x＞2$时，$h'(x)＞0$，此时函数$h(x)$单调递增，所以$\ln a\leqslant h(x)_{\min}=h(2)=2$，解得$a\leqslant\mathrm{e}^{2}$.综上，$0＜a\leqslant\mathrm{e}^{2}$.故选A.