《2026年一本密卷高考数学》

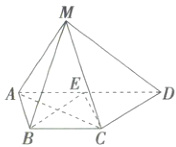
25. 在四棱锥 $ M - ABCD $ 中，$ AD = 4 $，$ AB = BC = 2 $，$ \angle BAD = 90^{\circ} $，$ BC// AD $，线段 $ AD $ 的中点为 $ E $，且 $ MC\perp BE $.
证明：平面 $ MAC\perp $ 平面 $ ACD $.

答案：
25. 证明：根据题意作出图形，如图，连接$CE$。
因为$E$是$AD$的中点，所以$AD = 2AE$。
因为$AD = 4$，所以$AE = 2$，
因为$BC = 2$，且$BC// AD$，所以$BC// AE$，且$BC = AE$，
所以四边形$ABCE$为平行四边形，
又$AB = BC$，$\angle BAD = 90°$，

所以四边形$ABCE$是正方形，所以$BE\perp AC$。
因为$MC\perp BE$，$MC$，$AC\subset$平面$MAC$，且$MC\cap AC = C$，
所以$BE\perp$平面$MAC$。
因为$BE\subset$平面$ABCD$，所以平面$MAC\perp$平面$ABCD$，
所以平面$MAC\perp$平面$ACD$。

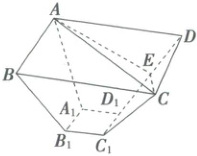
26. 如图，在底面为菱形的四棱台 $ ABCD - A_{1}B_{1}C_{1}D_{1} $ 中，点 $ E $ 为 $ DD_{1} $ 的中点，
(1) 证明：平面 $ ABB_{1}A_{1} $ 与平面 $ CDD_{1}C_{1} $ 的交线与 $ CD $ 平行；
(2) 在棱 $ CC_{1} $ 上是否存在一点 $ Q $，使得 $ BQ// $ 平面 $ AEC $？若存在，请证明；若不存在，请说明理由.

答案： 1. （1）证明：
因为四棱台$ABCD - A_{1}B_{1}C_{1}D_{1}$的底面$ABCD$是菱形，所以$AB// CD$。
又$AB\subset$平面$ABB_{1}A_{1}$，$CD\not\subset$平面$ABB_{1}A_{1}$，根据线面平行的判定定理$a\not\subset\alpha,b\subset\alpha,a// b\Rightarrow a//\alpha$，可得$CD//$平面$ABB_{1}A_{1}$。
设平面$ABB_{1}A_{1}\cap$平面$CDD_{1}C_{1}=l$，根据线面平行的性质定理$a//\alpha,a\subset\beta,\alpha\cap\beta = b\Rightarrow a// b$，因为$CD\subset$平面$CDD_{1}C_{1}$，所以$CD// l$。
2. （2）解：
存在，当$Q$为$CC_{1}$的中点时，$BQ//$平面$AEC$。
证明：
连接$BD$交$AC$于点$O$，连接$OE$。
因为底面$ABCD$是菱形，所以$O$是$BD$的中点。
又因为$E$是$DD_{1}$的中点，在$\triangle BDD_{1}$中，根据三角形中位线定理$EF// BC$，$EF=\frac{1}{2}BC$（这里$EF$类比$OE$，$BC$类比$BQ$相关线段关系），可得$OE// BQ$（通过构造平行四边形或利用中位线比例关系，在四棱台中，设$CC_{1}$中点为$Q$，连接$EQ$，$BQ$，$EQ// CD$，$EQ = \frac{1}{2}(CD + C_{1}D_{1})$，$OB// CD$，$OB=\frac{1}{2}CD$（四棱台上下底面平行且$CD// C_{1}D_{1}$），可证四边形$OBQE$是平行四边形）。
又$OE\subset$平面$AEC$，$BQ\not\subset$平面$AEC$，根据线面平行的判定定理$a\not\subset\alpha,b\subset\alpha,a// b\Rightarrow a//\alpha$，所以$BQ//$平面$AEC$。
综上，（1）得证；（2）存在，$Q$为$CC_{1}$中点。