2026年一本密卷高考数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年一本密卷高考数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 已知集合 $ A = \{ x | | x | < 3 \} $, $ B = \{ x \in \mathbf{N} | x ^ { 2 } < 11 \} $, 则 $ A \cap B = $ (
A.$ \{ - 2, - 1, 0, 1, 2, 3 \} $
B.$ \{ 0, 1, 2 \} $
C.$ \{ 1, 2, 3 \} $
D.$ \{ 1, 2 \} $
B
)A.$ \{ - 2, - 1, 0, 1, 2, 3 \} $
B.$ \{ 0, 1, 2 \} $
C.$ \{ 1, 2, 3 \} $
D.$ \{ 1, 2 \} $
答案:
1.B 因为$A=\{x||x|<3\}=\{x|-3<x<3\}$,$B=\{x\in \mathbf{N}|x^{2}<11\}=\{0,1,2,3\}$,所以$A\cap B =\{0,1,2\}$。故选B。
2. 设 $ i $ 为虚数单位, 复数 $ z $ 的共轭复数为 $ \overline { z } $, 若 $ \overline { z } = \frac { 2 + i } { i ^ { 2 0 2 3 } } $, 则 $ z $ 在复平面内对应的点位于第象限. (
A.一
B.二
C.三
D.四
A
)A.一
B.二
C.三
D.四
答案:
2.A 由题意得$\bar{z}=\frac{2+i}{1^{4× 506+1}}=\frac{2+i}{i}=1-2i$,所以$z =1 + 2i$,则$z$在复平面内对应的点位于第一象限。故选A。
3. 已知向量 $ a $, $ b $ 满足 $ | a | = 1 $, $ b = ( t, 2 - t ) $, $ a - b $ 与 $ a $ 垂直, 则 $ | a - b | $ 的最小值为 (
A.$ \sqrt { 2 } $
B.$ \frac { \sqrt { 2 } } { 2 } $
C.1
D.3
C
)A.$ \sqrt { 2 } $
B.$ \frac { \sqrt { 2 } } { 2 } $
C.1
D.3
答案:
3.C 由$\boldsymbol{a}-\boldsymbol{b}$与$\boldsymbol{a}$垂直,得$(\boldsymbol{a}-\boldsymbol{b})·\boldsymbol{a}=0$,则$\boldsymbol{a}·\boldsymbol{b}=\boldsymbol{a}^{2}=1$,所以$|\boldsymbol{a}-\boldsymbol{b}|=\sqrt{\boldsymbol{a}^{2}-2\boldsymbol{a}·\boldsymbol{b}+\boldsymbol{b}^{2}}=\sqrt{1^{2}-2×1× t^{2}+(2 - t)^{2}}=\sqrt{2(t - 1)^{2}+1}=1$,所以当$t = 1$时,$|\boldsymbol{a}-\boldsymbol{b}|$的最小值为$1$。故选C。
4. 二项式 $ \left( x + \frac { 1 } { \sqrt { x } } \right) ^ { 6 } $ 的展开式中, 把展开式中的项重新排列, 则有理项互不相邻的排法种数为 (
A.$ A _ { 7 } ^ { 7 } $ 种
B.$ A _ { 4 } ^ { 4 } A _ { 3 } ^ { 3 } $ 种
C.$ A _ { 4 } ^ { 4 } A _ { 3 } ^ { 3 } $ 种
D.$ A _ { 3 } ^ { 3 } A _ { 4 } ^ { 4 } $ 种
D
)A.$ A _ { 7 } ^ { 7 } $ 种
B.$ A _ { 4 } ^ { 4 } A _ { 3 } ^ { 3 } $ 种
C.$ A _ { 4 } ^ { 4 } A _ { 3 } ^ { 3 } $ 种
D.$ A _ { 3 } ^ { 3 } A _ { 4 } ^ { 4 } $ 种
答案:
4.D 二项式$(x+\frac{1}{\sqrt{x}})^{6}$的展开式的通项为:$T_{r + 1}=C_{6}^{r}· x^{6 - r}·(\frac{1}{\sqrt{x}})^{r}=C_{6}^{r}· x^{6-\frac{3r}{2}}(0\leq r\leq6,r\in\mathbf{N})$,令$6-\frac{3r}{2}\in\mathbf{Z}$,得$r\in\{0,2,4,6\}$,所以展开式中的有理项有$4$项,把展开式中的项重新排列,先把$3$项无理项全排列,再把$4$项有理项插入形成的$4$个空中,所以有理项互不相邻的排法种数为$A_{3}^{3}A_{4}^{4}$种。故选D。
5. 已知圆锥的底面半径为 3, 圆锥内的最大球的表面积为 $ 9 \pi $, 则该圆锥的侧面积为 (
A.$ 9 \pi $
B.$ 15 \pi $
C.$ 10 \sqrt { 2 } \pi $
D.$ 20 \sqrt { 3 } \pi $
B
)A.$ 9 \pi $
B.$ 15 \pi $
C.$ 10 \sqrt { 2 } \pi $
D.$ 20 \sqrt { 3 } \pi $
答案:
5.B 由球的表面积公式$S = 4\pi R^{2}=9\pi\Rightarrow R=\frac{3}{2}$,即圆锥内的最大球的直径为$\frac{3}{2}$,圆锥轴截面如图,则$AD = BD = 3$,$OD = OE=\frac{3}{2}$,因为$\angle COE+\angle DOE=\angle CAB+\angle DOE=\pi$,所以$\angle COE=\angle CAB$,设$\angle COE=\angle CAB = 2\alpha$,则$\sin\alpha=\frac{OD}{OA}=\frac{\frac{3}{2}}{\sqrt{(\frac{3}{2})^{2}+3^{2}}}=\frac{\sqrt{5}}{5}$,$\cos\alpha=\frac{AD}{OA}=\frac{3}{\sqrt{(\frac{3}{2})^{2}+3^{2}}}=\frac{2\sqrt{5}}{5}$,则$\cos2\alpha=\cos^{2}\alpha-\sin^{2}\alpha=\frac{3}{5}$。
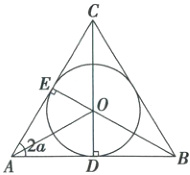
在$\triangle COE$中,$\cos2\alpha=\frac{OE}{OC}\Rightarrow OC=\frac{OE}{\cos2\alpha}=\frac{\frac{3}{2}}{\frac{3}{5}}=\frac{5}{2}$,所以$CD = CO + OD = 4$,所以$BC=\sqrt{CD^{2}+BD^{2}}=5$,所以圆锥的侧面积为$\pi×3×5 = 15\pi$。故选B。
5.B 由球的表面积公式$S = 4\pi R^{2}=9\pi\Rightarrow R=\frac{3}{2}$,即圆锥内的最大球的直径为$\frac{3}{2}$,圆锥轴截面如图,则$AD = BD = 3$,$OD = OE=\frac{3}{2}$,因为$\angle COE+\angle DOE=\angle CAB+\angle DOE=\pi$,所以$\angle COE=\angle CAB$,设$\angle COE=\angle CAB = 2\alpha$,则$\sin\alpha=\frac{OD}{OA}=\frac{\frac{3}{2}}{\sqrt{(\frac{3}{2})^{2}+3^{2}}}=\frac{\sqrt{5}}{5}$,$\cos\alpha=\frac{AD}{OA}=\frac{3}{\sqrt{(\frac{3}{2})^{2}+3^{2}}}=\frac{2\sqrt{5}}{5}$,则$\cos2\alpha=\cos^{2}\alpha-\sin^{2}\alpha=\frac{3}{5}$。

在$\triangle COE$中,$\cos2\alpha=\frac{OE}{OC}\Rightarrow OC=\frac{OE}{\cos2\alpha}=\frac{\frac{3}{2}}{\frac{3}{5}}=\frac{5}{2}$,所以$CD = CO + OD = 4$,所以$BC=\sqrt{CD^{2}+BD^{2}}=5$,所以圆锥的侧面积为$\pi×3×5 = 15\pi$。故选B。
6. 设椭圆 $ C : \frac { x ^ { 2 } } { a ^ { 2 } } + \frac { y ^ { 2 } } { b ^ { 2 } } = 1 ( a > b > 0 ) $ 的一个焦点为 $ F $, 点 $ O $ 为坐标原点, 若 $ C $ 上存在点 $ P $ 使得 $ \triangle O P F $ 为等边三角形, 则 $ C $ 的离心率为 (
A.$ \frac { 1 } { 2 } $
B.$ \frac { \sqrt { 3 } } { 2 } $
C.$ \sqrt { 3 } - 1 $
D.$ \frac { \sqrt { 3 } + 1 } { 4 } $
C
)A.$ \frac { 1 } { 2 } $
B.$ \frac { \sqrt { 3 } } { 2 } $
C.$ \sqrt { 3 } - 1 $
D.$ \frac { \sqrt { 3 } + 1 } { 4 } $
答案:
6.C 设椭圆的另一焦点为$F_{1}$,连接$F_{1}P$如图所示。
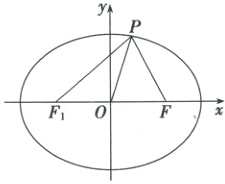
因为$\triangle OPF$为等边三角形,所以$|OF_{1}|=|OF|=|OP|=c$,所以$\angle F_{1}PF = 90^{\circ}$,又因为$\angle PFO = 60^{\circ}$,所以$|PF_{1}|=\sin60^{\circ}×|F_{1}F|=\sqrt{3}c$,由椭圆定义可知$|PF| = 2a-|PF_{1}|=2a-\sqrt{3}c = c$,整理,得$\frac{c}{a}=\frac{2}{\sqrt{3}+1}=\sqrt{3}-1$。故选C。
6.C 设椭圆的另一焦点为$F_{1}$,连接$F_{1}P$如图所示。

因为$\triangle OPF$为等边三角形,所以$|OF_{1}|=|OF|=|OP|=c$,所以$\angle F_{1}PF = 90^{\circ}$,又因为$\angle PFO = 60^{\circ}$,所以$|PF_{1}|=\sin60^{\circ}×|F_{1}F|=\sqrt{3}c$,由椭圆定义可知$|PF| = 2a-|PF_{1}|=2a-\sqrt{3}c = c$,整理,得$\frac{c}{a}=\frac{2}{\sqrt{3}+1}=\sqrt{3}-1$。故选C。
7. 已知函数 $ f ( x ) = \cos ( \omega x + \varphi ) \left( \omega > 0, - \frac { \pi } { 2 } < \varphi < 0 \right) $, $ \left| f \left( - \frac { \pi } { 6 } \right) \right| = 1 $, $ f \left( \frac { \pi } { 6 } \right) = 0 $, 且 $ f ( x ) $ 在区间 $ \left( \frac { \pi } { 6 }, \frac { 5 \pi } { 2 4 } \right) $ 上单调, 则 $ \omega $ 的最大值为 (
A.$ \frac { 9 } { 2 } $
B.$ \frac { 2 1 } { 2 } $
C.$ \frac { 3 3 } { 2 } $
D.$ \frac { 4 5 } { 2 } $
B
)A.$ \frac { 9 } { 2 } $
B.$ \frac { 2 1 } { 2 } $
C.$ \frac { 3 3 } { 2 } $
D.$ \frac { 4 5 } { 2 } $
答案:
7.B 由题意知,$\frac{\pi}{6}-(-\frac{\pi}{6})=(2k + 1)×\frac{T}{4}(k\in\mathbf{Z})$,则$T=\frac{4\pi}{3(2k + 1)}$,因为$T=\frac{2\pi}{|\omega|}$,所以$\omega=\frac{3(2k + 1)}{2}$,又因为$f(x)$在区间$(\frac{\pi}{6},\frac{5\pi}{24})$上单调,所以$\frac{5\pi}{24}-\frac{\pi}{6}\leq\frac{T}{4}$,解得$0<\omega\leq12$,则$\omega$的最大值为$\frac{21}{2}$。故选B。
8. 已知函数 $ f ( x ) ( f ( x ) $ 不恒为零), 其中 $ f ^ { \prime } ( x ) $ 为 $ f ( x ) $ 的导函数, 对于任意的 $ x, y \in \mathbf { R } $, 满足 $ f ( x + y ) f ( x - y ) = f ^ { 2 } ( x ) - f ^ { 2 } ( y ) $, 且 $ f ( 1 ) = 2 $, $ f ( 2 ) = 0 $, 则 (
A.$ f ( 0 ) = 1 $
B.$ f ( x + 4 ) $ 是偶函数
C.$ f ^ { \prime } ( x + 1 ) $ 关于点 $ ( 1, 0 ) $ 对称
D.$ \sum _ { k = - 1 } ^ { 1 2 } f ( k ) = - 2 $
D
)A.$ f ( 0 ) = 1 $
B.$ f ( x + 4 ) $ 是偶函数
C.$ f ^ { \prime } ( x + 1 ) $ 关于点 $ ( 1, 0 ) $ 对称
D.$ \sum _ { k = - 1 } ^ { 1 2 } f ( k ) = - 2 $
答案:
8.D A选项:由$f(x + y)f(x - y)=f^{2}(x)-f^{2}(y)$,令$x = y = 0$,则$f^{2}(0)=f^{2}(0)-f^{2}(0)=0$,即$f(0)=0$,A选项错误;
B选项:令$x = 0$,可知$f(y)f(-y)=-f^{2}(y)$,又$f(y)$不恒为$0$,则$f(-y)=-f(y)$,所以函数$f(x)$为奇函数。令$\begin{cases}x = 1 + t\\y = 1 - t\end{cases}$,则$f(2)· f(2t)=f^{2}(1 + t)-f^{2}(1 - t)=0$,即$f^{2}(1 + t)=f^{2}(1 - t)$,即$f^{2}(2 - x)=f^{2}(x)$,又$f(2 + x)f(2 - x)=-f^{2}(x)=-f^{2}(2 - x)$,则$f(2 + x)=-f(2 - x)$,所以$f(x + 4)=-f(-x)=f(x)$,所以$f(x + 4)$为奇函数,B选项错误;
C选项:由B选项可知$f(2 + x)=-f(2 - x)$,两边同时求导可知$f^{\prime}(2 + x)=f^{\prime}(2 - x)$,即函数$f^{\prime}(x)$关于直线$x = 2$对称,所以函数$f^{\prime}(x + 1)$关于直线$x = 1$对称,C选项错误;
D选项:由B选项可知$f(x + 4)=f(x)$,即函数$f(x)$的一个周期$T = 4$,由上述分析和已知条件,$f(-1)+f(1)=0$,$f(0)=f(2)=0$,所以$\sum_{k = -1}^{12}f(k)=f(-1)+f(0)+f(1)+f(2)+·s+f(11)+f(12)=3[f(-1)+f(0)+f(1)+f(2)]+f(-1)+f(0)=0 - f(1)-0=-2$,D选项正确。故选D。
B选项:令$x = 0$,可知$f(y)f(-y)=-f^{2}(y)$,又$f(y)$不恒为$0$,则$f(-y)=-f(y)$,所以函数$f(x)$为奇函数。令$\begin{cases}x = 1 + t\\y = 1 - t\end{cases}$,则$f(2)· f(2t)=f^{2}(1 + t)-f^{2}(1 - t)=0$,即$f^{2}(1 + t)=f^{2}(1 - t)$,即$f^{2}(2 - x)=f^{2}(x)$,又$f(2 + x)f(2 - x)=-f^{2}(x)=-f^{2}(2 - x)$,则$f(2 + x)=-f(2 - x)$,所以$f(x + 4)=-f(-x)=f(x)$,所以$f(x + 4)$为奇函数,B选项错误;
C选项:由B选项可知$f(2 + x)=-f(2 - x)$,两边同时求导可知$f^{\prime}(2 + x)=f^{\prime}(2 - x)$,即函数$f^{\prime}(x)$关于直线$x = 2$对称,所以函数$f^{\prime}(x + 1)$关于直线$x = 1$对称,C选项错误;
D选项:由B选项可知$f(x + 4)=f(x)$,即函数$f(x)$的一个周期$T = 4$,由上述分析和已知条件,$f(-1)+f(1)=0$,$f(0)=f(2)=0$,所以$\sum_{k = -1}^{12}f(k)=f(-1)+f(0)+f(1)+f(2)+·s+f(11)+f(12)=3[f(-1)+f(0)+f(1)+f(2)]+f(-1)+f(0)=0 - f(1)-0=-2$,D选项正确。故选D。
9. 某农业研究所为了解种植新品种玉米的亩产量情况, 从某地区随机抽查 100 亩种植新品种玉米的亩产量(单位: $ \mathrm { kg } $ ), 整理出如下统计表:

已知这 100 亩的亩产量均在 $[ 8 0 0, 1 4 0 0 ] $ 内, 根据表中数据, 下列结论正确的是 (
A.这 100 亩种植新品种玉米的亩产量的极差介于 $ 400 \mathrm { kg } $ 至 $ 600 \mathrm { kg } $ 之间
B.这 100 亩种植新品种玉米的亩产量的中位数大于 $ 1 1 0 0 \mathrm { kg } $
C.估计该地区种植新品种玉米的亩产量不低于 $ 1 0 0 0 \mathrm { kg } $ 的占比为 $ 7 0 \% $
D.估计该地区种植新品种玉米的亩产量的平均值介于 $ 1 1 5 0 \mathrm { kg } $ 至 $ 1 2 0 0 \mathrm { kg } $ 之间

已知这 100 亩的亩产量均在 $[ 8 0 0, 1 4 0 0 ] $ 内, 根据表中数据, 下列结论正确的是 (
AC
)A.这 100 亩种植新品种玉米的亩产量的极差介于 $ 400 \mathrm { kg } $ 至 $ 600 \mathrm { kg } $ 之间
B.这 100 亩种植新品种玉米的亩产量的中位数大于 $ 1 1 0 0 \mathrm { kg } $
C.估计该地区种植新品种玉米的亩产量不低于 $ 1 0 0 0 \mathrm { kg } $ 的占比为 $ 7 0 \% $
D.估计该地区种植新品种玉米的亩产量的平均值介于 $ 1 1 5 0 \mathrm { kg } $ 至 $ 1 2 0 0 \mathrm { kg } $ 之间
答案:
9.AC 由表中数据可知,这$100$亩种植新品种玉米的亩产量的极差小于等于$1400 - 800 = 600$,大于$1300 - 900 = 400$,故A正确;由表可知,$20 + 15 + 5<50$,所以亩产量的中位数小于$1100kg$,故B错误;估计该地区种植新品种玉米亩的产量不低于$1000kg$的占比为$1 - 10\% - 20\% = 70\%$,故C正确;根据表中数据,亩产量在$[1000,1100)$的有$100 - 10 - 20 - 20 - 15 - 5 = 30$,估计该地区种植新品种玉米的亩产量的平均数$\bar{x}<\frac{10×900 + 20×1000 + 30×1100 + 20×1200 + 15×1300 + 5×1400}{100}=1125$,故D错误。故选AC。
查看更多完整答案,请扫码查看


