《2026年一本密卷高考数学》

27. 如图，在矩形 $ AA_1D_1D $ 中，$\overrightarrow{AE}=\overrightarrow{ED}$，$\overrightarrow{B_1D_1}=2\overrightarrow{A_1B_1}$，$AE = 3$，$AB_1 = 2\sqrt{3}$。把该矩形折起，形成一个正三棱柱 $ ABC - A_1B_1C_1 $，其中点 $ D $，$ D_1 $ 分别与 $ A $，$ A_1 $ 重合，且点 $ F $ 为该正三棱柱的棱 $ A_1C_1 $ 的中点。
(1) 求正三棱柱 $ ABC - A_1B_1C_1 $ 的体积；
(2) 求异面直线 $ AF $ 和 $ BC $ 所成角的余弦值；
(3) 求平面 $ AEF $ 与平面 $ ABB_1 $ 的夹角的正弦值。

答案：
27.解：
(1)根据题意构造正三棱柱，如图所示，其中$AB=2$，$BE=1$，$AB_1=2\sqrt{3}$，
则$AA_1^2=AB_1^2 - A_1B_1^2=(2\sqrt{3})^2 - 2^2=8$，
得$AA_1=2\sqrt{2}$.
所以正三棱柱$ABC - A_1B_1C_1$的体积$V = S_{\triangle ABC}×AA_1=\frac{1}{2}×2×2×\frac{\sqrt{3}}{2}×2\sqrt{2}=2\sqrt{6}$.
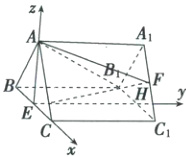
(2)取$B_1C_1$的中点$H$，连接$EH$，则$EH// BB_1$，所以$EH\perp$平面$ABC$，所以$EH\perp EA$，$EH\perp EC$.又$AE\perp BC$，故以点$E$为原点，分别以$EC$，$EH$，$EA$的方向为$x$轴，$y$轴，$z$轴的正方向建立如图所示的空间直角坐标系.
则$E(0,0,0)$，$A(0,0,\sqrt{3})$，$B(-1,0,0)$，$C(1,0,0)$，$B_1(-1,2\sqrt{2},0)$，$A_1(0,2\sqrt{2},\sqrt{3})$，$C_1(1,2\sqrt{2},0)$，$F(\frac{1}{2},2\sqrt{2},\frac{\sqrt{3}}{2})$，
则$\overrightarrow{AF}=(\frac{1}{2},2\sqrt{2},-\frac{\sqrt{3}}{2})$，$\overrightarrow{BC}=(2,0,0)$，
所以$|\overrightarrow{AF}| = 3$，$|\overrightarrow{BC}| = 2$，$\overrightarrow{AF}·\overrightarrow{BC}=1$，
所以$|\cos\langle\overrightarrow{AF},\overrightarrow{BC}\rangle|=\frac{|\overrightarrow{AF}·\overrightarrow{BC}|}{|\overrightarrow{AF}|·|\overrightarrow{BC}|}=\frac{1}{6}$，
所以异面直线$AF$和$BC$所成角的余弦值为$\frac{1}{6}$.

(3)由
(2)可知$\overrightarrow{EA}=(0,0,\sqrt{3})$，$\overrightarrow{EF}=(\frac{1}{2},2\sqrt{2},\frac{\sqrt{3}}{2})$.设平面$AEF$的法向量为$\mathbf{n}=(x,y,z)$，
则$\begin{cases}\overrightarrow{EA}·\mathbf{n}=\sqrt{3}z = 0\\\overrightarrow{EF}·\mathbf{n}=\frac{1}{2}x + 2\sqrt{2}y + \frac{\sqrt{3}}{2}z = 0\end{cases}$
取$y = 1$，得$x = -4\sqrt{2}$，$z = 0$，
则平面$AEF$的一个法向量为$\mathbf{n}=(-4\sqrt{2},1,0)$.
同理，由
(2)可知$\overrightarrow{AB_1}=(-1,2\sqrt{2},-\sqrt{3})$，$\overrightarrow{BB_1}=(0,2\sqrt{2},0)$.
设平面$ABB_1$的法向量为$\mathbf{m}=(x_1,y_1,z_1)$，
则$\begin{cases}\overrightarrow{AB_1}·\mathbf{m}=-x_1 + 2\sqrt{2}y_1 - \sqrt{3}z_1 = 0\\\overrightarrow{BB_1}·\mathbf{m}=2\sqrt{2}y_1 = 0\end{cases}$
取$z_1 = 1$，得$x_1 = -\sqrt{3}$，$y_1 = 0$，
则平面$ABB_1$的一个法向量为$\mathbf{m}=(-\sqrt{3},0,1)$.
所以$\cos\langle\mathbf{m},\mathbf{n}\rangle=\frac{\mathbf{m}·\mathbf{n}}{|\mathbf{m}|·|\mathbf{n}|}=\frac{4\sqrt{6}}{2×\sqrt{33}}=\frac{2\sqrt{22}}{11}$.
设平面$AEF$与平面$ABB_1$的夹角为$\theta$，
则$\sin\theta=\sqrt{1 - \cos^2\langle\mathbf{m},\mathbf{n}\rangle}=\sqrt{1 - (\frac{2\sqrt{22}}{11})^2}=\frac{\sqrt{33}}{11}$，
所以平面$AEF$与平面$ABB_1$的夹角的正弦值为$\frac{\sqrt{33}}{11}$.