2026年一本密卷高考数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年一本密卷高考数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
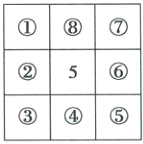
9. (2025·四川省德阳市三模)根据洛书记载:“以五居中,五方皆为阳数,四隅皆为阴数”意为九宫格中 5 位于居中位置,四个顶角填偶数,其余位置填奇数(用完 1 到 9 九个数字). 按洛书的填写方法,记事件 $A$ =“满足图案中每行、每列及对角线上的三个数字和都相等,且 $a + b\geqslant 9$”,则 $P(A)=$

$\frac{1}{96}$
.
答案:
9.$\frac{1}{96}$ 九宫格的中间填5,①③⑤⑦位置填偶数2,4,6,8,②④⑥⑧位置填奇数1,3,7,9,故总的情况共有$A_4^4 A_4^4 = 24×24$种情况。要使每一横行,每一竖列以及两条对角线上三个数字之和都相等,则和为15,所以①⑤、③⑦位置填2,8或4,6;满足$a + b \geq 9$,则③处填的数字不大于6,故符合条件的情况有以下类型:
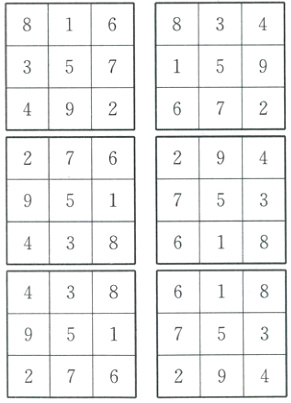
因此,符合条件的有6种情况,故概率为$P(A) = \frac{6}{24×24} = \frac{1}{96}$。
9.$\frac{1}{96}$ 九宫格的中间填5,①③⑤⑦位置填偶数2,4,6,8,②④⑥⑧位置填奇数1,3,7,9,故总的情况共有$A_4^4 A_4^4 = 24×24$种情况。要使每一横行,每一竖列以及两条对角线上三个数字之和都相等,则和为15,所以①⑤、③⑦位置填2,8或4,6;满足$a + b \geq 9$,则③处填的数字不大于6,故符合条件的情况有以下类型:


因此,符合条件的有6种情况,故概率为$P(A) = \frac{6}{24×24} = \frac{1}{96}$。
10. (2025·江苏如皋市三模)已知一个黑色袋子里装有 2 个红球,4 个白球,这些球除颜色不同外,其余均相同,甲同学每次从袋子中任取一个球,不放回,直到把两个红球都取出来即终止,记此时袋子里剩余球的个数为 $X$. 则随机变量 $X$ 的期望是
$\frac{4}{3}$
.
答案:
10.$\frac{4}{3}$ $X$的可能取值为0,1,2,3,4
$P(X = 0) = \frac{C_2^1 C_5^1 A_4^4}{A_6^6} = \frac{1}{3}$;
$P(X = 1) = \frac{C_2^1 C_1^1 A_4^4}{A_6^6} = \frac{4}{15}$;
$P(X = 2) = \frac{C_2^1 C_1^1 A_4^4}{A_6^6} = \frac{1}{5}$;
$P(X = 3) = \frac{C_2^2 A_4^4}{A_6^6} = \frac{2}{15}$;
$P(X = 4) = \frac{A_2^2 A_4^4}{A_6^6} = \frac{1}{15}$。
随机变量$X$的分布列为:
|$X$|0|1|2|3|4|
|----|----|----|----|----|----|
|$P$|$\frac{1}{3}$|$\frac{4}{15}$|$\frac{1}{5}$|$\frac{2}{15}$|$\frac{1}{15}$|
$E(X) = 1×\frac{4}{15} + 2×\frac{1}{5} + 3×\frac{2}{15} + 4×\frac{1}{15} = \frac{4}{3}$
$P(X = 0) = \frac{C_2^1 C_5^1 A_4^4}{A_6^6} = \frac{1}{3}$;
$P(X = 1) = \frac{C_2^1 C_1^1 A_4^4}{A_6^6} = \frac{4}{15}$;
$P(X = 2) = \frac{C_2^1 C_1^1 A_4^4}{A_6^6} = \frac{1}{5}$;
$P(X = 3) = \frac{C_2^2 A_4^4}{A_6^6} = \frac{2}{15}$;
$P(X = 4) = \frac{A_2^2 A_4^4}{A_6^6} = \frac{1}{15}$。
随机变量$X$的分布列为:
|$X$|0|1|2|3|4|
|----|----|----|----|----|----|
|$P$|$\frac{1}{3}$|$\frac{4}{15}$|$\frac{1}{5}$|$\frac{2}{15}$|$\frac{1}{15}$|
$E(X) = 1×\frac{4}{15} + 2×\frac{1}{5} + 3×\frac{2}{15} + 4×\frac{1}{15} = \frac{4}{3}$
11. (13 分)(2025·湖南省郴州市三模)某兴趣小组调查了某校 100 名学生 100 米短跑成绩的情况,其中有 60 名学生的短跑成绩合格. 这 100 名学生中有 45 名学生每周的锻炼时间超过 5 小时,60 名短跑成绩合格的学生中有 35 名学生每周的锻炼时间超过 5 小时.
(1)根据所给数据,完成以下表格,依据小概率值 $\alpha = 0.005$ 的 $\chi^{2}$ 独立性检验,是否可以推断学生短跑成绩合格与每周的锻炼时间超过 5 小时有关?单位:人

(2)正确的跑步姿势和起跑技巧等都可以让跑步者更好地发挥自己的能力. 现对短跑成绩不合格的学生进行跑步技巧培训,已知每周的锻炼时间超过 5 小时的学生参加跑步技巧培训后,学生的短跑成绩合格的概率为 $\frac{5}{6}$,每周的锻炼时间不超过 5 小时的学生参加跑步技巧培训后,学生的短跑成绩合格的概率为 $\frac{3}{4}$. 用频率代替概率,从短跑成绩不合格的学生中随机抽取 1 名学生(记为甲)进行跑步技巧培训,求学生甲参加培训后短跑成绩合格的概率.
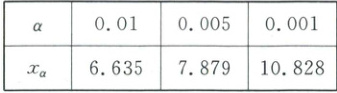
参考公式与数据:$\chi^{2}=\frac{n(ad - bc)^{2}}{(a + b)(c + d)(a + c)(b + d)}$,其中 $n = a + b + c + d$.
(1)根据所给数据,完成以下表格,依据小概率值 $\alpha = 0.005$ 的 $\chi^{2}$ 独立性检验,是否可以推断学生短跑成绩合格与每周的锻炼时间超过 5 小时有关?单位:人

(2)正确的跑步姿势和起跑技巧等都可以让跑步者更好地发挥自己的能力. 现对短跑成绩不合格的学生进行跑步技巧培训,已知每周的锻炼时间超过 5 小时的学生参加跑步技巧培训后,学生的短跑成绩合格的概率为 $\frac{5}{6}$,每周的锻炼时间不超过 5 小时的学生参加跑步技巧培训后,学生的短跑成绩合格的概率为 $\frac{3}{4}$. 用频率代替概率,从短跑成绩不合格的学生中随机抽取 1 名学生(记为甲)进行跑步技巧培训,求学生甲参加培训后短跑成绩合格的概率.
参考公式与数据:$\chi^{2}=\frac{n(ad - bc)^{2}}{(a + b)(c + d)(a + c)(b + d)}$,其中 $n = a + b + c + d$.

答案:
11.解:
(1)表格如下:
单位:人
|每周的锻炼时间|短跑成绩合格|短跑成绩不合格|合计|
|----|----|----|----|
|每周的锻炼时间超过5小时|35|10|45|
|每周的锻炼时间不超过5小时|25|30|55|
|合计|60|40|100|
零假设为$H_0$:学生短跑成绩合格与每周锻炼时间相互独立。根据表中的数据,可得$\chi^2 = \frac{100×(35×30 - 25×10)^2}{60×40×45×55} = \frac{3200}{297} \approx 10.774 > 7.879 = \chi_{0.005}$,根据小概率值$\alpha = 0.005$的$\chi^2$独立性检验,可以推断$H_0$不成立,即认为学生短跑成绩合格与每周的锻炼时间超过5小时有关。
(2)由
(1)的列联表可知,短跑成绩不合格的学生共有40名,其每周锻炼时间超过5小时的有10人,不超过5小时的有30人。从短跑成绩不合格的40名学生中随机抽取一名学生,记为甲。
设事件A = “甲参加跑步技巧培训后短跑成绩合格”,事件B = “甲每周的锻炼时间超过5小时”,$\overline{B}$ = “甲每周的锻炼时间不超过5小时”,用列联表中的数据计算频率并替代概率后得$P(B) = \frac{10}{40} = \frac{1}{4}$,$P(\overline{B}) = \frac{30}{40} = \frac{3}{4}$。又已知$P(A|B) = \frac{5}{6}$,$P(A|\overline{B}) = \frac{3}{4}$,由全概率公式可得$P(A) = P(B)P(A|B) + P(\overline{B})P(A|\overline{B}) = \frac{1}{4}×\frac{5}{6} + \frac{3}{4}×\frac{3}{4} = \frac{37}{48}$,所以学生甲参加跑步技巧培训后短跑成绩合格的概率为$\frac{37}{48}$。
(1)表格如下:
单位:人
|每周的锻炼时间|短跑成绩合格|短跑成绩不合格|合计|
|----|----|----|----|
|每周的锻炼时间超过5小时|35|10|45|
|每周的锻炼时间不超过5小时|25|30|55|
|合计|60|40|100|
零假设为$H_0$:学生短跑成绩合格与每周锻炼时间相互独立。根据表中的数据,可得$\chi^2 = \frac{100×(35×30 - 25×10)^2}{60×40×45×55} = \frac{3200}{297} \approx 10.774 > 7.879 = \chi_{0.005}$,根据小概率值$\alpha = 0.005$的$\chi^2$独立性检验,可以推断$H_0$不成立,即认为学生短跑成绩合格与每周的锻炼时间超过5小时有关。
(2)由
(1)的列联表可知,短跑成绩不合格的学生共有40名,其每周锻炼时间超过5小时的有10人,不超过5小时的有30人。从短跑成绩不合格的40名学生中随机抽取一名学生,记为甲。
设事件A = “甲参加跑步技巧培训后短跑成绩合格”,事件B = “甲每周的锻炼时间超过5小时”,$\overline{B}$ = “甲每周的锻炼时间不超过5小时”,用列联表中的数据计算频率并替代概率后得$P(B) = \frac{10}{40} = \frac{1}{4}$,$P(\overline{B}) = \frac{30}{40} = \frac{3}{4}$。又已知$P(A|B) = \frac{5}{6}$,$P(A|\overline{B}) = \frac{3}{4}$,由全概率公式可得$P(A) = P(B)P(A|B) + P(\overline{B})P(A|\overline{B}) = \frac{1}{4}×\frac{5}{6} + \frac{3}{4}×\frac{3}{4} = \frac{37}{48}$,所以学生甲参加跑步技巧培训后短跑成绩合格的概率为$\frac{37}{48}$。
查看更多完整答案,请扫码查看


