《2026年一本密卷高考数学》

1. (2025·天津市滨海新区三模)已知 $m,n$ 是两条不同的直线，$\alpha,\beta$ 是两个不同的平面，则下列命题正确的是(C)

A.若 $m// \alpha,n\subset \alpha$，则 $m// n$
B.若 $m// \alpha,m// n$，则 $n// \alpha$
C.若 $m\perp \alpha,n\perp \beta,m\perp n$，则 $\alpha\perp \beta$
D.若 $\alpha\perp \beta,\alpha\cap \beta = l,m\perp l$，则 $m\perp \alpha$

答案： 1.C　对于A，由$m// \alpha$，$n \subset \alpha$，则$m// n$或$m$，$n$异面，故A错误；对于B，由$m// \alpha$，$m// n$，则$n// \alpha$或$n \subset \alpha$，故B错误；对于C，由$m \perp \alpha$，$m \perp n$，则$n// \alpha$或$n \subset \alpha$，则在平面$\alpha$内存在直线$a// n$，而$n \perp \beta$，则$a\perp \beta$，所以$\alpha \perp \beta$，故C正确；对于D，由$\alpha \perp \beta$，$\alpha \cap \beta = l$，$m \perp l$，只有当$m \subset \beta$或$m// \beta$时，$m \perp \alpha$，故D错误.故选C.

2. (2025·山东省枣庄市三模)已知圆锥的体积为 $\frac{2\sqrt{2}\pi}{3}$，其侧面展开图是一个圆心角为 $\frac{2\pi}{3}$ 的扇形，则该圆锥的底面半径为(B)

A.$\frac{1}{2}$
B.1
C.$\sqrt{2}$
D.2

答案： 2.B　设母线长为$l$，底面半径为$r$，圆锥的高为$h$，则有$2\pi r = \frac{2\pi}{3}l \Rightarrow l = 3r$，又$h = \sqrt{l^{2} - r^{2}} = \sqrt{9r^{2} - r^{2}} = 2\sqrt{2}r$，所以$V = \frac{1}{3}Sh = \frac{1}{3}\pi r^{2} × 2\sqrt{2}r = \frac{2\sqrt{2}\pi r^{3}}{3}=1 \Rightarrow r^{3} =1 \Rightarrow r = 1$.故选B.

3. (2025·山东省泰安市三模)已知正三棱柱的表面积为 $6\sqrt{3}$，则当其体积取得最大值时，该三棱柱的高为(B)

A.3
B.$\frac{2\sqrt{3}}{3}$
C.$\frac{4\sqrt{3}}{3}$
D.$\frac{5\sqrt{2}}{4}$

答案： 3.B　设正三棱柱的底面边长为$a$，高为$h$，则其表面积$S = 2 × \frac{\sqrt{3}}{4}a^{2} + 3ah = 6\sqrt{3}$，得$h = \frac{12 - a^{2}}{2\sqrt{3}a}$，又$h ＞0$，所以$0 ＜ a ＜ 2\sqrt{3}$，故正三棱柱的体积$V = \frac{\sqrt{3}}{4}a^{2}h =\frac{12a - a^{3}}{8}$，则$V'(a) = \frac{3}{2} - \frac{3}{8}a^{2}$，当$0 ＜ a ＜ 2$时，$V'(a) ＞ 0$，$V(a)$单调递增，当$2 ＜ a ＜ 2\sqrt{3}$时，$V'(a) ＜ 0$，$V(a)$单调递减，所以当$a = 2$时，该正三棱柱体积取得最大值，此时三棱柱的高为$\frac{2\sqrt{3}}{3}$.故选B.

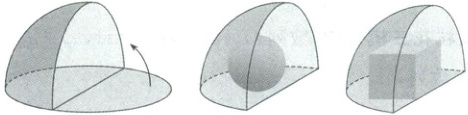
4. (2025·辽宁沈阳三模)如图，一个四分之一球形状的玩具储物盒，若放入一个玩具小球，合上盒盖. 可放小球的最大半径为 $r$. 若是放入一个正方体，合上盒盖，可放正方体的最大棱长为 $a$，则 $\frac{r}{a} =$(D)


A.$2 + \sqrt{2}$
B.$2 - \sqrt{2}$
C.$\frac{3}{2}(\sqrt{2} + 1)$
D.$\frac{3}{2}(\sqrt{2} - 1)$

答案：
4.D　设储物盒所在球的半径为$R$，如图，
　　 　　
小球最大半径$r$满足$(\sqrt{2} + 1)r = R$，所以$r = \frac{R}{\sqrt{2} + 1}= (\sqrt{2} - 1)R$，正方体的最大棱长$a$满足$(\sqrt{2}a)^{2} + (\frac{a}{2})^{2} = R^{2}$，解得$a = \frac{2}{3}R$，所以$\frac{r}{a} = \frac{\sqrt{2} - 1}{\frac{2}{3}} = \frac{3}{2}(\sqrt{2}-1)$.故选D.

5. (2025·河北石家庄三模)在如图所示的试验装置中，正方形框架 $ABCD$ 的边长为 2，长方形框架 $ABEF$ 的长 $BE = \frac{3}{2}AB$，且它们所在平面形成的二面角 $C - AB - E$ 的大小为 $\frac{\pi}{3}$，活动弹子 $M,N$ 分别在对角线 $AC$ 和 $BF$ 上移动，且始终保持 $\frac{AM}{AC} = \frac{BN}{BF} = a$($0 ＜ a ＜ 1$)，则 $MN$ 的长度最小时 $a$ 的取值为(A)


A.$\frac{8}{23}$
B.$\frac{6}{23}$
C.$\frac{6}{15}$
D.$\frac{2}{15}$

答案： 5.A　由题意知，$AB \perp BC$，$AB \perp BE$，$\therefore \angle CBE$就是二面角$C - AB - E$的平面角，即$\angle CBE = \frac{\pi}{3}$，以$B$为原点，以$BA,BE$所在直线分别为$x,y$轴，过$B$点作$z$轴$\perp$平面$ABEF$，建立如图所示的空间直角坐标系，则$B(0,0,0)$，$A(2,0,0)$，$C(0,1,\sqrt{3})$，$F(2,3,0)$，$\therefore \overrightarrow{AC} = (-2,1,\sqrt{3})$，$\overrightarrow{BF} = (2,3,0)$，设$M(x,y,z)$，$N(m,n,0)$，由$\frac{AM}{AC} = \frac{BN}{BF} = a(0 ＜ a ＜1)$，可知$\overrightarrow{AM} = a\overrightarrow{AC}$，$\overrightarrow{BN} = a\overrightarrow{BF}$，$\therefore (x - 2,y,z) = a(-2,1,\sqrt{3})$，$(m,n,0) = a(2,3,0)$，$\therefore\begin{cases} x - 2 = - 2a \\y = a \\z = \sqrt{3}a \end{cases}$，$\begin{cases} m = 2a \\n = 3a \end{cases}$，解得$x = 2 - 2a$，$M(2 - 2a,a,\sqrt{3}a)$，$N(2a,3a,0)$，$\therefore |MN|^{2} = (2 - 2a - 2a)^{2} + (a - 3a)^{2} + (\sqrt{3}a)^{2}= 23a^{2} - 16a + 4 = 23(a - \frac{8}{23})^{2} + \frac{28}{23}$，$\therefore$当$a = \frac{8}{23}$时，$|MN|^{2}$取到最小值，即$MN$取到最小值.故选A.

6. (2025·山东省枣庄市三模)已知正方体 $ABCD - A_1B_1C_1D_1$ 的棱长为 1，点 $P$ 在正方体的内切球表面上运动，且满足 $BP//$ 平面 $ACD_1$，则下列结论不正确的是(B)

A.$BP\perp B_1D$
B.点 $P$ 的轨迹长度为 $\pi$
C.线段 $BP$ 长度的最小值为 $\frac{\sqrt{6}}{6}$
D.$\overrightarrow{BP}·\overrightarrow{BC_1}$ 的最小值为 $1 - \frac{\sqrt{3}}{3}$

答案：
6.B　以$D$为原点，分别以$DA,DC,DD_{1}$所在直线为$x,y,z$轴，建立空间直角坐标系，则$D(0,0,0)$，$A(1,0,0)$，$C(0,1,0)$，$B(1,1,0)$，$D_{1}(0,0,1)$，$B_{1}(1,1,1)$，$A_{1}(1,0,1)$，$C_{1}(0,1,1)$，正方体的内切球的球心为正方体的中心$O(\frac{1}{2},\frac{1}{2},\frac{1}{2})$，半径$r = \frac{1}{2}$，平面$ACD_{1}$的法向量$\mathbf{n}$，$\overrightarrow{AC} = (-1,1,0)$，$\overrightarrow{AD_{1}} = (-1,0,1)$，设$\mathbf{n} = (x,y,z)$，由$\begin{cases} \mathbf{n} · \overrightarrow{AC} = 0 \\\mathbf{n} · \overrightarrow{AD_{1}} = 0 \end{cases}$，即$\begin{cases} - x + y = 0 \\- x + z = 0 \end{cases}$，令$x = 1$，则$y = 1$，$z = 1$，所以$\mathbf{n} = (1,1,1)$.对于选项A，$\overrightarrow{B_{1}D} = (-1,-1,-1)$，因为$BP//$平面$ACD_{1}$，所以$\overrightarrow{BP} · \mathbf{n} = 0$，而$\overrightarrow{B_{1}D} = -\mathbf{n}$，所以$\overrightarrow{BP} · \overrightarrow{B_{1}D} = 0$，即$BP \perp B_{1}D$，A正确.对于选项B，因为$BP//$平面$ACD_{1}$，平面$ACD_{1}//$平面$A_{1}BC_{1}$，所以点$P$的轨迹是平面$A_{1}BC_{1}$与正方体内切球的交线，此交线为圆，记圆心为$O_{1}$.设平面$A_{1}BC_{1}$与正方体的中心$O$的距离$d$，设平面$A_{1}BC_{1}$的法向量为$\mathbf{m}$，$\overrightarrow{BA_{1}} = (0,-1,1)$，$\overrightarrow{BC_{1}} = (-1,0,1)$，设$\mathbf{m} = (a,b,c)$，由$\begin{cases} \mathbf{m} · \overrightarrow{BA_{1}} = 0 \\\mathbf{m} · \overrightarrow{BC_{1}} = 0 \end{cases}$，可得$\begin{cases} - b + c = 0 \\- a + c = 0 \end{cases}$，令$a = 1$，则$\mathbf{m} = (1,1,1)$.$\overrightarrow{OA_{1}} = (\frac{1}{2}, - \frac{1}{2},\frac{1}{2})$，$\therefore$点$O$到平面$A_{1}BC_{1}$的距离为$d = \frac{|\overrightarrow{OA_{1}} · \mathbf{m}|}{|\mathbf{m}|} =\frac{|\frac{1}{2} - \frac{1}{2} + \frac{1}{2}|}{\sqrt{3}} = \frac{\sqrt{3}}{6}$，$\therefore$圆$O_{1}$的半径为$r_{1} = \sqrt{r^{2} - d^{2}} = \sqrt{(\frac{1}{2})^{2} - (\frac{\sqrt{3}}{6})^{2}} = \frac{\sqrt{6}}{6}$，圆的周长$l = 2\pi r_{1}= \frac{\sqrt{6}}{3}\pi$，即点$P$的轨迹长度为$\frac{\sqrt{6}}{3}\pi$，B错误.对于选项C，$BO_{1} = \sqrt{BO^{2} - d^{2}} =\sqrt{(\frac{\sqrt{3}}{2})^{2} - (\frac{\sqrt{3}}{6})^{2}} = \frac{\sqrt{6}}{3}$，点$P$在球面上，$BO = \sqrt{BO^{2} - d^{2}} =\sqrt{(\frac{\sqrt{3}}{2})^{2} - (\frac{\sqrt{3}}{6})^{2}} = \frac{\sqrt{6}}{3}$，线段$BP$长度的最小值为$BO_{1} - \frac{\sqrt{6}}{3} = \frac{\sqrt{6}}{3} - \frac{\sqrt{6}}{3} = \frac{\sqrt{6}}{3}$，C选项正确.对于选项D，设$\overrightarrow{BP}$与$\overrightarrow{BC_{1}}$夹角为$\theta$，$\overrightarrow{BC_{1}} = (-1,0,1)$，$|\overrightarrow{BC_{1}}| =\sqrt{2}$.在平面直角坐标系中，$B(0,\frac{\sqrt{6}}{2})$，$C_{1}( - \frac{\sqrt{2}}{2},0)$，$P(x,y)$，$O_{1}(0,\frac{\sqrt{6}}{6})$，$\overrightarrow{BC} = ( - \frac{\sqrt{2}}{2}, - \frac{\sqrt{6}}{2})$，$\overrightarrow{BP} =(x,y - \frac{\sqrt{6}}{2})$，所以$x^{2} + (y - \frac{\sqrt{6}}{2})^{2} = (\frac{\sqrt{6}}{6})^{2}$，令$x = \frac{\sqrt{6}}{6}\cos\theta$，$y = \frac{\sqrt{6}}{6}\sin\theta + \frac{\sqrt{6}}{2}$，$\overrightarrow{BP} · \overrightarrow{BC} = - \frac{\sqrt{2}}{2}x - \frac{\sqrt{6}}{2}y + \frac{3}{2} = 1 - \frac{\sqrt{3}}{3}\sin(\theta + \frac{\pi}{6}) \geq 1 - \frac{\sqrt{3}}{3}$，所以$\overrightarrow{BP} · \overrightarrow{BC}$的最小值为$1 - \frac{\sqrt{3}}{3}$，D选项正确.故选B.
　　 　　

7. (2025·四川省宜宾市三模)“阿基米德多面体”也称半正多面体，是由两种或多种正多边形面组成，而又不属于正多面体的凸多面体，体现了数学的对称美. 如图，某广场的一张石凳就是一个阿基米德多面体，它是由正方体截去八个一样的四面体得到的二十四等边体，若它所有的棱长都为 2，则(ABC)


A.该石凳的表面积为 $24 + 8\sqrt{3}$
B.该石凳的体积为 $\frac{40\sqrt{2}}{3}$
C.直线 $LH$ 与 $BC$ 的夹角为 $60^{\circ}$
D.$DH\perp$ 平面 $LEI$

答案：
7.ABC　对于A，由图可知，二十四等边体是由6个边长为2的正方形和8个边长为2的等边三角形围成，所以表面积为$6 × 2 × 2 + 8 × \frac{1}{2} × 2 × 2\sin 60^{\circ}= 24 + 8\sqrt{3}$，A正确；对于B，补全八个角构成一个棱长为$2\sqrt{2}$的一个正方体，则该正方体的体积为$V =(2\sqrt{2})^{3} = 16\sqrt{2}$，其中每个小三棱锥的体积为$V_{1} =\frac{1}{3} × \frac{1}{2} × \sqrt{2} × \sqrt{2} × \sqrt{2} = \frac{\sqrt{2}}{3}$，所以该二十四面体的体积为$16\sqrt{2} - 8 × \frac{\sqrt{2}}{3} = \frac{40\sqrt{2}}{3}$，所以B正确；
　　　　　　
对于C，补全八个角构成一个棱长为$2\sqrt{2}$的一个正方体，如图，易知$LH// FC$，$FC$与$BC$所成角为$60^{\circ}$，所以直线$LH$与$BC$的夹角为$60^{\circ}$，C正确；对于D，由正方体易知：$DH// BE$，$LI// AB$，$AB$，$EB$所成角为$60^{\circ}$，所以$DH$，$LI$所成角为$60^{\circ}$，又$LI$在平面$LEI$内，所以$DH \perp$平面$LEI$不成立，故D错误.故选ABC.