《2026年一本密卷高考数学》

9. (多选)2024 年 12 月，DeepSeek 正式上线全新系列大语言模型 DeepSeek - V3，其具备多语言对话、实时信息检索、复杂逻辑推理和创意内容生成等能力，该大语言模型算法降低了应用门槛，预测未来 AI 应用上限将更高.某校科技兴趣小组设计调查问卷调查本校学生对“大语言模型”的了解程度，被调查学生所得分数 $ X $ 可近似看作服从正态分布 $ N(76,225) $，则(附：若随机变量 $ X\sim N(\mu,\sigma^{2}) $，则 $ P(\mu-\sigma\leqslant X\leqslant\mu + \sigma)\approx 0.6827 $，$ P(\mu - 2\sigma\leqslant X\leqslant\mu + 2\sigma)\approx 0.9545 $，$ P(\mu - 3\sigma\leqslant X\leqslant\mu + 3\sigma)\approx 0.9973 $)(ABD)

A.$ P(X ＜ 20) = P(X ＞ 132) $
B.$ P(X ＞ 30) ＞ P(X ＜ 120) $
C.$ P(46\leqslant X\leqslant 106) = 0.8186 $
D.$ P(31\leqslant X\leqslant 91) = 0.84 $

答案： 9. ABD $\frac{20 + 132}{2} = 76$，故$P(X ＜ 20) = P(X ＞ 132)$，故A正确。$\frac{30 + 122}{2} = 76$，$P(X ＞ 30) = P(X ＜ 122) ＞ P(X ＜ 120)$，故B正确。$\mu = 76$，$\sigma = 15$，$P(46\leq X\leq 106) = P(\mu - 2\sigma\leq X\leq \mu + 2\sigma)\approx 0.9545$，故C错误。$P(31\leq X\leq 91) = P(\mu - 3\sigma\leq X\leq \mu + \sigma)\approx \frac{0.6827 + 0.9973}{2} = 0.84$，故D正确。故选ABD。

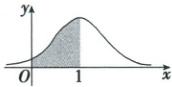
10. (多选)已知正态分布 $ N(1,\sigma^{2}) $ 的正态密度曲线如图所示，$ X\sim N(1,\sigma^{2}) $，则下列选项中，可以表示图中阴影部分面积的是(ABD)


A.$ \frac{1}{2}-P(X\leqslant 0) $
B.$ \frac{1}{2}-P(X\geqslant 2) $
C.$ \frac{1}{2}-P(1\leqslant X\leqslant 2) $
D.$ \frac{1}{2}P(X\leqslant 2)-\frac{1}{2}P(X\leqslant 0) $

答案： 10. ABD 正态分布$N(1, \sigma^2)$的正态密度曲线关于直线$x = 1$对称，可得图中阴影部分的面积为$P(0\leq X\leq 1)$，可表示为$P(0\leq X\leq 1) = P(X\leq 1) - P(X\leq 0) = \frac{1}{2} - P(X\leq 0) = \frac{1}{2} - P(X\geq 2)$，故AB正确。对C，由对称性可得$\frac{1}{2} - P(1\leq X\leq 2) = P(X\geq 2) = P(X\leq 0)$，故C错误。对D，由对称性可得$P(0\leq X\leq 1) = P(1\leq X\leq 2)$，所以$P(0\leq X\leq 1) = \frac{1}{2}[P(X\leq 2) - P(X\leq 0)]$，故D正确。故选ABD。

11. 已知 $ a·\log_{3}4 = 1 $，$ b·\log_{4}5 = 1 $，$ c· e^{0.02} = 1 $，则（ ）

A.$ a ＞ b ＞ c $
B.$ b ＞ a ＞ c $
C.$ c ＞ b ＞ a $
D.$ b ＞ c ＞ a $

答案： 11. C 由题意可得$a = \log_4 3$，$b = \log_5 4$，则$a$，$b$均在0和1之间，$\frac{a}{b} = \log_4 3·\log_4 5 ＜ (\frac{\log_4 3 + \log_4 5}{2})^2 = (\frac{\log_4 15}{2})^2 = (\log_4 \sqrt{15})^2 ＜ 1$，故$a ＜ b$。
当$x ＜ 0$时，令$f(x) = e^x - x - 1$，
则$f'(x) = e^x - 1 ＜ 0$，所以$f(x)$在$(-\infty, 0)$上单调递减，
故$f(x) ＞ e^0 - 0 - 1 = 0$，故$e^x ＞ x + 1$，
所以$c = e^{-0.02} ＞ -0.02 + 1 = 0.98$，
$b = \log_5 4 = 2\log_5 2 = \frac{2}{9}\log_5 2^9 = \frac{2}{9}\log_5 512 ＜ \frac{2}{9}\log_5 5^4 = \frac{8}{9} ＜ 0.9$，
故$c ＞ b$。所以$c ＞ b ＞ a$。故选C。

12. 已知 $ a = \sqrt{e} $，$ b = \frac{3}{2} $，$ c = 2\ln 2 $，则（ ）

A.$ b ＜ c ＜ a $
B.$ a ＜ c ＜ b $
C.$ c ＜ a ＜ b $
D.$ c ＜ b ＜ a $

答案： 12. D 令$f(x) = e^x - x - 1$，则$f'(x) = e^x - 1$，当$x ＜ 0$时，$f'(x) ＜ 0$，当$x ＞ 0$时，$f'(x) ＞ 0$，所以$f(x)$在$(-\infty, 0)$上单调递减，在$(0, +\infty)$上单调递增，
所以$f(x)\geq f(0)$，即$e^x - x - 1\geq e^0 - 0 - 1 = 0$，所以$e^x\geq x + 1$，当且仅当$x = 0$时取等号，
故当$x = \frac{1}{2}$时，$\sqrt{e} = e^{\frac{1}{2}} ＞ \frac{1}{2} + 1 = \frac{3}{2}$，所以$a ＞ b$。
令$g(x) = \ln x - \frac{1}{e}x(x ＞ 0)$，则$g'(x) = \frac{1}{x} - \frac{1}{e}$，
当$0 ＜ x ＜ e$时，$g'(x) ＞ 0$，当$x ＞ e$时，$g'(x) ＜ 0$，
所以$g(x)$在$(0, e)$上单调递增，在$(e, +\infty)$上单调递减，所以$g(x)\leq g(e)$，即$\ln x - \frac{1}{e}x\leq \ln e - \frac{1}{e}× e = 0$，所以$\ln x\leq \frac{1}{e}x$，当且仅当$x = e$时取等号，所以$2\ln 2 = \ln 4 ＜ \frac{1}{e}× 4 ＜ \frac{3}{2}$，所以$c ＜ b$，所以$c ＜ b ＜ a$。故选D。