《2025年周末C计划高中数学必修第一册人教版》

1. （2023全国乙理，2）设全集$U = \mathbf{R}$，集合$M = \{ x | x ＜ 1 \}$，$N = \{ x | - 1 ＜ x ＜ 2 \}$，则$\{ x | x \geq 2 \} =$（ ）

A.$\complement _ { U } ( M \cup N )$
B.$N \cup \complement _ { U } M$
C.$\complement _ { U } ( M \cap N )$
D.$M \cup \complement _ { U } N$

答案：
1.A
解法一：由题意可得$M \cup N = \{x \mid x ＜ 2\}$，则$\complement_U(M \cup N) = \{x \mid x \geq 2\}$，选项 A 正确；
$\complement_U M = \{x \mid x \geq 1\}$，则$N \cup \complement_U M = \{x \mid x ＞ -1\}$，选项 B 错误；
$M \cap N = \{x \mid -1 ＜ x ＜ 1\}$，则$\complement_U(M \cap N) = \{x \mid x \leq -1或x \geq 1\}$，选项 C 错误；
$\complement_U N = \{x \mid x \leq -1或x \geq 2\}$，则$M \cup \complement_U N = \{x \mid x ＜ 1或x \geq 2\}$，选项 D 错误。
解法二(数形结合法)：将集合$M$、$N$在数轴上表示出来，如图所示：

通过数轴可知，$\{x \mid x \geq 2\} = \complement_U(M \cup N)$。
易错警示：利用数轴表示集合时，空心圆圈表示不包含该元素，实心圆点表示包含该元素。

2. （2023北京，8）若$xy \neq 0$，则“$x + y = 0$”是“$\frac { y } { x } + \frac { x } { y } = - 2$”的（C）
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件

答案： 2.C
解法一：先判断充分性，因为$x + y = 0$，所以$x = -y$，所以$\frac{y}{x} + \frac{x}{y} = \frac{-x}{x} + \frac{x}{-x} = -1 - 1 = -2$，所以充分性成立；
再判断必要性，因为$\frac{y}{x} + \frac{x}{y} = -2$，所以$x^2 + y^2 = -2xy$，即$x^2 + y^2 + 2xy = 0$，即$(x + y)^2 = 0$，所以$x + y = 0$，所以必要性成立。
所以“$x + y = 0$”是“$\frac{y}{x} + \frac{x}{y} = -2$”的充要条件。
解法二：先判断充分性，因为$x + y = 0$，所以$\frac{y}{x} + \frac{x}{y}=\frac{y^2 + x^2}{xy}=\frac{x^2 + y^2 + 2xy - 2xy}{xy}=\frac{(x + y)^2 - 2xy}{xy}=\frac{(x + y)^2}{xy} - 2 = -2$，所以充分性成立；
再判断必要性，因为$\frac{y}{x} + \frac{x}{y} = -2$，所以$\frac{y}{x} + \frac{x}{y} = \frac{y^2 + x^2}{xy}= \frac{x^2 + y^2 + 2xy - 2xy}{xy} = \frac{(x + y)^2 - 2xy}{xy} = \frac{(x + y)^2}{xy} - 2 = -2$，所以$\frac{(x + y)^2}{xy} = 0$，所以$(x + y)^2 = 0$，所以$x + y = 0$，所以必要性成立。
所以“$x + y = 0$”是“$\frac{y}{x} + \frac{x}{y} = -2$”的充要条件。

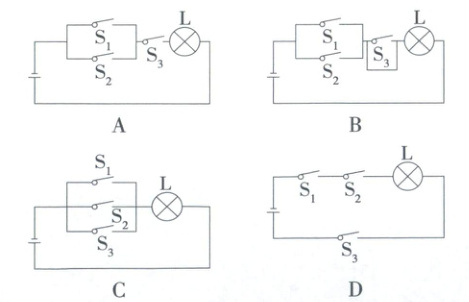
3. 设计如图所示的四个电路图，条件$p$：“灯泡$\mathrm{L}$亮”，条件$q$：“开关$\mathrm{S}_{1}$闭合”，条件$r$：“开关$\mathrm{S}_{3}$闭合”，则满足$q$是$p$的充分不必要条件，且$r$是$p$的既不充分也不必要条件的电路图是（B）

答案： 3.B
对于 A，灯泡 L 亮，可能是$S_1$，$S_3$闭合，也可能是$S_2$，$S_3$闭合，也可能是$S_1$，$S_2$，$S_3$均闭合，故$S_1$不一定闭合；当$S_1$闭合时，若$S_3$未闭合，则灯泡 L 不亮，故$q$是$p$的既不充分也不必要条件，A 错误。
对于 B，由于$S_1$和$S_2$是并联关系，$S_3$与它们串联，但其下方是闭合通路，故$S_1$闭合时，灯泡 L 亮；当灯泡 L 亮时，$S_1$不一定闭合，可能是$S_2$闭合，故$q$是$p$的充分不必要条件；由题图知$S_3$是否闭合不影响灯泡 L，所以$r$是$q$的既不充分也不必要条件，B 正确。
对于 C，由于$S_1$，$S_2$，$S_3$是并联关系，故当$S_1$或$S_3$闭合时，灯泡 L 亮，当灯泡 L 亮时，$S_1$或$S_3$不一定闭合，可能是$S_2$闭合，故$q$是$p$的充分不必要条件，$r$是$p$的充分不必要条件，C 错误；
对于 D，由于$S_1$，$S_2$，$S_3$和 L 是串联关系，故灯泡 L 亮，必有$S_1$，$S_2$，$S_3$均闭合，但当$S_1$或$S_3$闭合，$S_2$未闭合时，灯泡 L 不亮，即$q$是$p$的必要不充分条件，且$r$是$p$的必要不充分条件，D 错误。

4. （2025河北唐山第一中学月考）设$a$，$b \in \mathbf{R}$，集合$A = \{ a, a ^ { 2 } + 1 \}$，$B = \{ b, b ^ { 2 } + 1 \}$，则“$A = B$”是“$a = b$”的（C）
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件

答案： 4.C
因为$A = \{a, a^2 + 1\}$，$B = \{b, b^2 + 1\}$，所以当$A = B$时，有$\begin{cases}a = b, \\a^2 + 1 = b^2 + 1\end{cases}$或$\begin{cases}a = b^2 + 1, \\a^2 + 1 = b\end{cases}$
由$\begin{cases}a = b, \\a^2 + 1 = b^2 + 1\end{cases}$得$a = b$；
由$\begin{cases}a = b^2 + 1, \\a^2 + 1 = b\end{cases}$得$(b^2 + 1)^2 + 1 = b$，整理得$(b^2 - b + 1)(b^2 + b + 2) = 0$，因为$b^2 - b + 1 = (b - \frac{1}{2})^2 + \frac{3}{4} ＞ 0$，$b^2 + b + 2 =(b + \frac{1}{2})^2 + \frac{7}{4} ＞ 0$，所以$(b^2 - b + 1)(b^2 + b + 2) = 0$无解。
综上可得当$A = B$时，有$a = b$，即充分性成立。
当$a = b$时，显然有$A = B$，即必要性成立。
所以“$A = B$”是“$a = b$”的充要条件。

5. （2025福建莆田第二中学期中）已知非空集合$A \subseteq \mathbf{R}$，且$A$满足如下性质：若$a$，$b \in A$，则$a + b \in A$；若$a \in A$，则$- a \in A$，可称集合$A$为一个“群”.以下叙述正确的个数为（C）
①若$A$为一个“群”，则$A$必为无限集；
②若$A$为一个“群”，且$a$，$b \in A$，则$a - b \in A$；
③若$A$，$B$都是“群”，则$A \cap B$必定是“群”.
A.$0$
B.$1$
C.$2$
D.$3$

答案： 5.C
对于①，设集合$A = \{0\}$，显然符合题中两性质，因此集合$A = \{0\}$是一个“群”，但是它是有限集，故本叙述不正确；
对于②，根据“群”的性质，由$b \in A$可得$-b \in A$，因此可得$a - b \in A$，故本叙述正确；
对于③，设$A \cap B = C$，$c \in C$，则一定有$c \in A$，$c \in B$，因为$A$，$B$都是“群”，所以$-c \in A$，$-c \in B$，因此$-c \in C$，若$d \in C$，则$d \in A$，$d \in B$，故$c + d \in A$，$c + d \in B$，所以$c + d \in C$，故本叙述正确。
综上，叙述正确的个数为 2。

6. （2025上海交大附中等四校期中联考）设$A _ { 1 }$，$A _ { 2 }$，$A _ { 3 }$，$···$，$A _ { 7 }$均是含有$2$个元素的集合，且$A _ { 1 } \cap A _ { 7 } = \varnothing$，$A _ { i } \cap A _ { i + 1 } = \varnothing ( i = 1,2,3,···,6 )$，记$B = A _ { 1 } \cup A _ { 2 } \cup A _ { 3 } \cup ··· \cup A _ { 7 }$，则$B$中元素个数的最小值是（5）
A.$4$
B.$5$
C.$6$
D.$7$

答案： 6.B
$\because A_i \cap A_{i + 1} = \varnothing (i = 1,2,3,·s,6)$，
$\therefore A_1$与$A_2$的元素不同，则$A_1 \cup A_2$中的元素个数为 4，若$B$中元素个数的最小值是 4，则只能是$A_1 = A_3 = A_5 = A_7$，$A_2 = A_4 = A_6$，与$A_1 \cap A_7 = \varnothing$矛盾。
若$A_3$的元素是从$A_1$中选择 1 个元素，再加入一个新元素，则$A_1 \cup A_2 \cup A_3$的元素个数为 5，将这 5 个元素适当排列，可得到符合题意的$A_4$，$A_5$，$A_6$，$A_7$，例如$A_1 = \{1,2\}$，$A_2 = \{3,4\}$，$A_3 = \{1,5\}$，不妨取$A_4 = \{2,4\}$，$A_5 = \{3,5\}$，$A_6 = \{1,2\}$，$A_7 = \{3,5\}$，符合题意，故$B$中元素个数的最小值是 5。

7. （2025江苏扬州中学期中）用$C ( A )$表示非空集合$A$中的元素的个数，定义$A * B = \left\{ \begin{array} { l } { C ( A ) - C ( B ), C ( A ) \geq C ( B ), } \\ { C ( B ) - C ( A ), C ( A ) ＜ C ( B ), } \end{array} \right.$已知集合$A = \{ x | x ^ { 2 } + x = 0 \}$，$B = \{ x \in \mathbf{R} | ( x ^ { 2 } + a x ) ( x ^ { 2 } + a x + 1 ) = 0 \}$，则下列结论正确的是（ACD）
A.$\exists a \in \mathbf{R}$，$C ( B ) = 3$
B.$\forall a \in \mathbf{R}$，$C ( B ) \geq 2$
C.“$a = 0$”是“$A * B = 1$”的充分不必要条件
D.若$S = \{ a \in \mathbf{R} | A * B = 1 \}$，则$C ( S ) = 3$

答案： 7.ACD
对于 A，当$a = 2$时，$B = \{-2, -1, 0\}$，此时$C(B) = 3$，故 A 正确。
对于 B，当$a = 0$时，$B = \{0\}$，此时$C(B) = 1$，故 B 不正确。
对于 C，$A = \{-1, 0\}$，则$C(A) = 2$，由 B 知当$a = 0$时，$C(B) = 1$，所以$A * B = 1$；当$A * B = 1$时，因为$C(A) = 2$，所以$C(B) = 1$或$C(B) = 3$，若$C(B) = 1$，则$\begin{cases}a = 0, \\a^2 - 4 ＜ 0\end{cases}$，若$C(B) = 3$，因为方程$x^2 + ax = 0$的两个根$x = 0$和$x = -a$都不是方程$x^2 + ax + 1 = 0$的根，所以需满足$\begin{cases}a \neq 0, \\a^2 - 4 = 0\end{cases}$，解得$a = \pm 2$，所以“$a = 0$”是“$A * B = 1$”的充分不必要条件，故 C 正确。
对于 D，因为$A * B = 1$，所以由 C 可知，$a = 0$或$a = \pm 2$，所以$S = \{-2, 0, 2\}$，所以$C(S) = 3$，故 D 正确。

8. 已知非空集合$A$，$B$，定义$A - B = \{ x | x \in A$且$x \notin B \}$，$A \otimes B = \{ x | x \in A \cup B$且$x \notin A \cap B \}$，则下列结论一定正确的是（BCD）
A.$\complement _ { A } ( A - B ) = B$
B.$A \otimes B = ( A - B ) \cup ( B - A )$
C.当$A \otimes B = B - A$时，$A \subseteq B$
D.当$A - B = B - A$时，$A \otimes B = \varnothing$

答案： 8.BCD
对于 A，由$A - B = \{x \mid x \in A且x \notin B\}$，得$\complement_A(A - B) = \{x \mid x \in A \cap B\}$，A 错误；
对于 B，设$x \in A \otimes B$，则$x \in A \cup B$且$x \notin A \cap B$，因此$x \in A$且$x \notin B$或$x \in B$且$x \notin A$，即$x \in A - B$或$x \in B - A$，则$x \in (A - B) \cup (B - A)$，因此$A \otimes B \subseteq (A - B) \cup (B - A)$，反之，若$x \in (A - B) \cup (B - A)$，则$x \in A - B$或$x \in B - A$，即$x \in A$且$x \in B$，或$x \in B$且$x \notin A$，则$x \in A \cup B$且$x \notin A \cap B$，因此$(A - B) \cup (B - A) \subseteq A \otimes B$，所以$A \otimes B = (A - B) \cup (B - A)$，B 正确；
对于 C，结合 B 知$A \otimes B = (A - B) \cup (B - A) = B - A$，则$(A - B) \subseteq (B - A)$，所以若$x \in A - B$，则$x \in B - A$，由$A = (A - B) \cup (A \cap B)$，得对任意的$x \in A$，有$x \in A - B$或$x \in A \cap B$，又$B = (B - A) \cup (A \cap B)$，所以$x \in B$，所以$A \subseteq B$，C 正确；
对于 D，由题知对任意的$x \in A$，有$x \in A - B$或$x \in A \cap B$，又$A - B = B - A$，所以$x \in B - A$或$x \in A \cap B$，所以$x \in B$，所以$A \subseteq B$，同理，$B \subseteq A$，所以$A = B$，所以$A \cup B = A \cap B$，从而$A \otimes B = \varnothing$，D 正确。
名师指点：本题考查集合的新定义，解题关键是正确理解新定义，把两个新定义运算和集合的交集与并集运算相结合，把新定义运算转化为元素与集合间的关系，达到解题目的。