2025年周末C计划高中数学必修第一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年周末C计划高中数学必修第一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
17. (15 分)(2025 山东菏泽期末)已知函数$f(x)$是定义在$\mathbf{R}$上的奇函数,当$x\gt0$时,$f(x)=-x + 3$.
(1)求函数$f(x)$的解析式;
(2)若关于$x$的方程$f(x^{2}+1)+f(2kx)=0$在$(0,+\infty)$上有解,求实数$k$的取值范围.
(1)求函数$f(x)$的解析式;
(2)若关于$x$的方程$f(x^{2}+1)+f(2kx)=0$在$(0,+\infty)$上有解,求实数$k$的取值范围.
答案:
17.解析:
(1)$\because f(x)$是定义在$\mathbf{R}$上的奇函数,
$\therefore f(x) = - f( - x)$,$f(0) = 0$,(2分)
设$x < 0$,则$- x > 0$,$f( - x) = - ( - x) + 3 = x + 3$,
$\therefore f(x) = - f( - x) = - x - 3$,$x < 0$,(4分)
$\therefore f(x) = \begin{cases} - x - 3,x < 0, \\0,x = 0, \\ - x + 3,x > 0. \end{cases}$(5分)
(2)$\because x^{2} + 1 > 0$,$\therefore f(x^{2} + 1) = - (x^{2} + 1) + 3 = - x^{2} + 2$,(7分)
针对$k$与$0$的关系,分类讨论,脱去“$f$”,将抽象方程转化为具体方程。
①当$k > 0$时,$2kx > 0$在$(0, + \infty)$上恒成立,$\therefore f(2kx) = - 2kx + 3$,
方程$f(x^{2} + 1) + f(2kx) = 0$可化为$- x^{2} + 2 - 2kx + 3 = 0$,
即$x^{2} + 2kx - 5 = 0$,此时$\Delta = 4k^{2} + 20 > 0$,(9分)
所以方程$x^{2} + 2kx - 5 = 0$有两个不等的根,设为$x_{1}$,$x_{2}$,
则$x_{1}x_{2} = - 5 < 0$,所以$x_{1}$,$x_{2}$一正一负,
所以方程$f(x^{2} + 1) + f(2kx) = 0$在$(0, + \infty)$上有解,符合题意。(10分)
②当$k = 0$时,$f(2kx) = 0$,故方程$f(x^{2} + 1) + f(2kx) = 0$即为$- x^{2} + 2 = 0$,解得$x = \sqrt{2}$或$x = - \sqrt{2}$(舍去),符合题意。(12分)
③当$k < 0$时,$2kx < 0$在$(0, + \infty)$上恒成立,$\therefore f(2kx) = - 2kx - 3$,
$\therefore f(x^{2} + 1) + f(2kx) = - x^{2} + 2 - 2kx - 3 = - x^{2} - 2kx - 1$,
令$h(x) = - x^{2} - 2kx - 1$,其图象的对称轴方程为$x = - k > 0$,
$\because$方程$f(x^{2} + 1) + f(2kx) = 0$在$(0, + \infty)$上有解,$\therefore\Delta = 4k^{2} - 4 \geq 0$,解得$k \leq - 1$或$k \geq 1$,$\therefore k \leq - 1$。(14分)
综上所述,$k$的取值范围是$\{ k|k \leq - 1$或$k \geq 0\}$。(15分)
(1)$\because f(x)$是定义在$\mathbf{R}$上的奇函数,
$\therefore f(x) = - f( - x)$,$f(0) = 0$,(2分)
设$x < 0$,则$- x > 0$,$f( - x) = - ( - x) + 3 = x + 3$,
$\therefore f(x) = - f( - x) = - x - 3$,$x < 0$,(4分)
$\therefore f(x) = \begin{cases} - x - 3,x < 0, \\0,x = 0, \\ - x + 3,x > 0. \end{cases}$(5分)
(2)$\because x^{2} + 1 > 0$,$\therefore f(x^{2} + 1) = - (x^{2} + 1) + 3 = - x^{2} + 2$,(7分)
针对$k$与$0$的关系,分类讨论,脱去“$f$”,将抽象方程转化为具体方程。
①当$k > 0$时,$2kx > 0$在$(0, + \infty)$上恒成立,$\therefore f(2kx) = - 2kx + 3$,
方程$f(x^{2} + 1) + f(2kx) = 0$可化为$- x^{2} + 2 - 2kx + 3 = 0$,
即$x^{2} + 2kx - 5 = 0$,此时$\Delta = 4k^{2} + 20 > 0$,(9分)
所以方程$x^{2} + 2kx - 5 = 0$有两个不等的根,设为$x_{1}$,$x_{2}$,
则$x_{1}x_{2} = - 5 < 0$,所以$x_{1}$,$x_{2}$一正一负,
所以方程$f(x^{2} + 1) + f(2kx) = 0$在$(0, + \infty)$上有解,符合题意。(10分)
②当$k = 0$时,$f(2kx) = 0$,故方程$f(x^{2} + 1) + f(2kx) = 0$即为$- x^{2} + 2 = 0$,解得$x = \sqrt{2}$或$x = - \sqrt{2}$(舍去),符合题意。(12分)
③当$k < 0$时,$2kx < 0$在$(0, + \infty)$上恒成立,$\therefore f(2kx) = - 2kx - 3$,
$\therefore f(x^{2} + 1) + f(2kx) = - x^{2} + 2 - 2kx - 3 = - x^{2} - 2kx - 1$,
令$h(x) = - x^{2} - 2kx - 1$,其图象的对称轴方程为$x = - k > 0$,
$\because$方程$f(x^{2} + 1) + f(2kx) = 0$在$(0, + \infty)$上有解,$\therefore\Delta = 4k^{2} - 4 \geq 0$,解得$k \leq - 1$或$k \geq 1$,$\therefore k \leq - 1$。(14分)
综上所述,$k$的取值范围是$\{ k|k \leq - 1$或$k \geq 0\}$。(15分)
18. (17 分)(2025 广东东莞五校联考)东莞广播电视台旗下的电商平台——“家乡好物商城”依托广播、电视与互联网平台优势,主要销售东莞制造的优质产品及东莞对口支援、帮扶地区的农特产品,打通新疆、广西、云南、贵州等地区农特产品的产销对接渠道.近一个月来,“贵州黄牛肉”“广西小砂糖橘”“云南野苹果”等农特产品在东莞热销.通过对过去一个月(以 30 天计)的“广西小砂糖橘”的销售情况的调查发现:每千克的销售价格$P(x)$(单位:元)关于第$x$天$(1\leq x\leq30,x\in\mathbf{N}^{*})$的函数关系近似满足$P(x)=10+\frac{k}{x}(k\gt0)$,日销售量$Q(x)$(单位:千克)关于第$x$天的部分数据如下表所示:
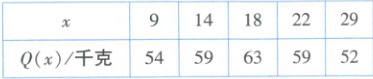
已知第 9 天的日销售收入为 552 元.
(1)求$k$的值;
(2)给出以下四种函数模型:
①$Q(x)=ax + b$;②$Q(x)=a|x - m|+b$;③$Q(x)=a^{x}+b$;④$Q(x)=b\log_{a}x$.
请你根据上表中的数据,从中选择你认为最合适的一种函数模型来描述日销售量$Q(x)$关于第$x$天的变化关系,并求出该函数的解析式;
(3)设该“广西小砂糖橘”的日销售收入为函数$y = f(x)$(单位:元),求函数$f(x)$的最小值.

已知第 9 天的日销售收入为 552 元.
(1)求$k$的值;
(2)给出以下四种函数模型:
①$Q(x)=ax + b$;②$Q(x)=a|x - m|+b$;③$Q(x)=a^{x}+b$;④$Q(x)=b\log_{a}x$.
请你根据上表中的数据,从中选择你认为最合适的一种函数模型来描述日销售量$Q(x)$关于第$x$天的变化关系,并求出该函数的解析式;
(3)设该“广西小砂糖橘”的日销售收入为函数$y = f(x)$(单位:元),求函数$f(x)$的最小值.
答案:
18.解析:
(1)由题意得$Q(9)P(9) = 552$,即$54 × (10 + \frac{k}{9}) = 552$,解得$k = 2$。(2分)
(2)由题表知,$Q(x)$的值随$x$值的增大先增大再减小,所以$Q(x) = a|x - m| + b$更合适。(4分)
把$(14,59)$,$(18,63)$,$(22,59)$代入,得$\begin{cases} a|14 - m| + b = 59, \\a|18 - m| + b = 63, \\a|22 - m| + b = 59, \end{cases}$解得$\begin{cases} m = 18, \\b = 63, \\a = - 1, \end{cases}$
所以$Q(x) = - |x - 18| + 63$。(7分)
经检验,$(9,54)$,$(29,52)$也满足上述解析式。(9分)
(3)由题意得,$f(x) = P(x)Q(x) = (10 + \frac{2}{x})( - |x - 18| + 63)$。(11分)
当$1 \leq x \leq 18$,$x \in \mathbf{N}^{*}$时,$f(x) = (10 + \frac{2}{x})[ - (18 - x) + 63] = 452 + 10x + \frac{90}{x} \geq 452 + 2\sqrt{10x · \frac{90}{x}} = 512$,
当且仅当$10x = \frac{90}{x}$,即$x = 3$时取等号,则$f(x)_{\min} = 512$。(13分)
当$18 < x \leq 30$,$x \in \mathbf{N}^{*}$时,$f(x) = (10 + \frac{2}{x})[ - (x - 18) + 63] = 808 - 10x + \frac{162}{x}$,显然$f(x)$单调递减,所以$f(x)_{\min} = f(30) = 513.4$。(15分)
因为$512 < 513.4$,
所以函数$f(x)$的最小值为$512$。(17分)
(1)由题意得$Q(9)P(9) = 552$,即$54 × (10 + \frac{k}{9}) = 552$,解得$k = 2$。(2分)
(2)由题表知,$Q(x)$的值随$x$值的增大先增大再减小,所以$Q(x) = a|x - m| + b$更合适。(4分)
把$(14,59)$,$(18,63)$,$(22,59)$代入,得$\begin{cases} a|14 - m| + b = 59, \\a|18 - m| + b = 63, \\a|22 - m| + b = 59, \end{cases}$解得$\begin{cases} m = 18, \\b = 63, \\a = - 1, \end{cases}$
所以$Q(x) = - |x - 18| + 63$。(7分)
经检验,$(9,54)$,$(29,52)$也满足上述解析式。(9分)
(3)由题意得,$f(x) = P(x)Q(x) = (10 + \frac{2}{x})( - |x - 18| + 63)$。(11分)
当$1 \leq x \leq 18$,$x \in \mathbf{N}^{*}$时,$f(x) = (10 + \frac{2}{x})[ - (18 - x) + 63] = 452 + 10x + \frac{90}{x} \geq 452 + 2\sqrt{10x · \frac{90}{x}} = 512$,
当且仅当$10x = \frac{90}{x}$,即$x = 3$时取等号,则$f(x)_{\min} = 512$。(13分)
当$18 < x \leq 30$,$x \in \mathbf{N}^{*}$时,$f(x) = (10 + \frac{2}{x})[ - (x - 18) + 63] = 808 - 10x + \frac{162}{x}$,显然$f(x)$单调递减,所以$f(x)_{\min} = f(30) = 513.4$。(15分)
因为$512 < 513.4$,
所以函数$f(x)$的最小值为$512$。(17分)
查看更多完整答案,请扫码查看


