2025年周末C计划高中数学必修第一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年周末C计划高中数学必修第一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
9. (2025 山东日照实验高级中学诊断)若$\alpha$、$\beta$两角的终边互为反向延长线,且$\alpha = - 120^{\circ}$,则符合条件的角$\beta$的一个值是
$60^{\circ}$(答案不唯一)
.
答案:
9.答案 $60^{\circ}$(答案不唯一)
解析 可取$\beta=\alpha + 180^{\circ}=60^{\circ}$.
名师指点
终边互为反向延长线的角有无数个,它们之间
相差$180^{\circ}$的奇数倍;终边在同一直线上的角之间相
差$180^{\circ}$的整数倍;终边相同的角相差$360^{\circ}$的整数倍.
解析 可取$\beta=\alpha + 180^{\circ}=60^{\circ}$.
名师指点
终边互为反向延长线的角有无数个,它们之间
相差$180^{\circ}$的奇数倍;终边在同一直线上的角之间相
差$180^{\circ}$的整数倍;终边相同的角相差$360^{\circ}$的整数倍.
10. (2025 黑龙江黑河龙西北名校联盟考试)某种药物作用在农作物上的分解率为 $v$,与时间 $t$ (小时)满足函数关系式$v = ab^{t}$ ($a$,$b$ 为非零常数),若经过 $12$ 小时该药物的分解率为 $10\%$,经过 $24$ 小时该药物的分解率为 $20\%$,那么这种药物完全分解至少需要经过
52
小时.(参考数据:$\lg 2 \approx 0.3$)
答案:
10.答案 $52$
解析 $\because$经过$12$小时该药物的分解率为$10\%$,经过
$24$小时该药物的分解率为$20\%$,
$\therefore\begin{cases}ab^{12}=0.1,\\ab^{24}=0.2,\end{cases}$解得$\begin{cases}a=\frac{1}{20},\\b=2^{\frac{1}{12}},\end{cases}$
当这种药物完全分解,即$v = 1$时,$\frac{1}{20}×(2^{\frac{1}{12}})^t=1$,得
$(2^{\frac{1}{12}})^t=20$,即$2^{\frac{t}{12}}=20^{12}$,两边取以$2$为底的对数得$t =\log_{2}20^{12}=12\log_{2}20 = 12×\frac{\lg20}{\lg2}=12×\frac{1 + \lg2}{\lg2}\approx12×\frac{1 + 0.3}{0.3}=52$.
解析 $\because$经过$12$小时该药物的分解率为$10\%$,经过
$24$小时该药物的分解率为$20\%$,
$\therefore\begin{cases}ab^{12}=0.1,\\ab^{24}=0.2,\end{cases}$解得$\begin{cases}a=\frac{1}{20},\\b=2^{\frac{1}{12}},\end{cases}$
当这种药物完全分解,即$v = 1$时,$\frac{1}{20}×(2^{\frac{1}{12}})^t=1$,得
$(2^{\frac{1}{12}})^t=20$,即$2^{\frac{t}{12}}=20^{12}$,两边取以$2$为底的对数得$t =\log_{2}20^{12}=12\log_{2}20 = 12×\frac{\lg20}{\lg2}=12×\frac{1 + \lg2}{\lg2}\approx12×\frac{1 + 0.3}{0.3}=52$.
11. (13 分)(2025 江西赣州中学开学检测)
(1)已知角$\alpha = 1200^{\circ}$,将$\alpha$改写成$\beta + 2k\pi(k \in \mathbf{Z},0 \leq \beta < 2\pi)$的形式,并指出$\alpha$是第几象限角;
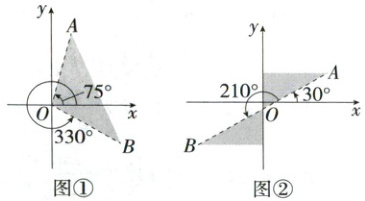
(2)用弧度表示终边落在如图所示阴影部分内(不包括边界)的角的集合.
(1)已知角$\alpha = 1200^{\circ}$,将$\alpha$改写成$\beta + 2k\pi(k \in \mathbf{Z},0 \leq \beta < 2\pi)$的形式,并指出$\alpha$是第几象限角;
(2)用弧度表示终边落在如图所示阴影部分内(不包括边界)的角的集合.

答案:
11.解析
(1)因为$\alpha = 1200^{\circ}=1200×\frac{\pi}{180}=\frac{20\pi}{3}=\frac{2\pi}{3}+3×2\pi$,
所以角$\alpha$与$\frac{2\pi}{3}$的终边相同,
又$\frac{\pi}{2}<\frac{2\pi}{3}<\pi$,所以角$\alpha$是第二象限角.
(2)题图①:因为$75^{\circ}=\frac{5\pi}{12},330^{\circ}=\frac{11\pi}{6}=2\pi-\frac{\pi}{6}$,
所以终边落在阴影部分内(不包括边界)的角的集合
为$\left\{\theta\mid2k\pi-\frac{\pi}{6}<\theta<2k\pi+\frac{5\pi}{12},k\in\mathbf{Z}\right\}$
$\rightarrow$表示终边相同的角时不要漏掉$k\in\mathbf{Z}$
题图②:因为$30^{\circ}=\frac{\pi}{6},90^{\circ}=\frac{\pi}{2},210^{\circ}=\frac{7\pi}{6}=\pi+\frac{\pi}{6}$,
$270^{\circ}=\frac{3\pi}{2}=\pi+\frac{\pi}{2}$,
所以终边落在阴影部分内(不包括边界)的角的集合
为$\left\{\theta\mid k\pi+\frac{\pi}{6}<\theta<k\pi+\frac{\pi}{2},k\in\mathbf{Z}\right\}$
(1)因为$\alpha = 1200^{\circ}=1200×\frac{\pi}{180}=\frac{20\pi}{3}=\frac{2\pi}{3}+3×2\pi$,
所以角$\alpha$与$\frac{2\pi}{3}$的终边相同,
又$\frac{\pi}{2}<\frac{2\pi}{3}<\pi$,所以角$\alpha$是第二象限角.
(2)题图①:因为$75^{\circ}=\frac{5\pi}{12},330^{\circ}=\frac{11\pi}{6}=2\pi-\frac{\pi}{6}$,
所以终边落在阴影部分内(不包括边界)的角的集合
为$\left\{\theta\mid2k\pi-\frac{\pi}{6}<\theta<2k\pi+\frac{5\pi}{12},k\in\mathbf{Z}\right\}$
$\rightarrow$表示终边相同的角时不要漏掉$k\in\mathbf{Z}$
题图②:因为$30^{\circ}=\frac{\pi}{6},90^{\circ}=\frac{\pi}{2},210^{\circ}=\frac{7\pi}{6}=\pi+\frac{\pi}{6}$,
$270^{\circ}=\frac{3\pi}{2}=\pi+\frac{\pi}{2}$,
所以终边落在阴影部分内(不包括边界)的角的集合
为$\left\{\theta\mid k\pi+\frac{\pi}{6}<\theta<k\pi+\frac{\pi}{2},k\in\mathbf{Z}\right\}$
12. (15 分)(2025 湖北云学名校联盟联考)“绿色出行,低碳环保”已成为新的时尚,近几年,国家相继出台了一系列的环保政策,在汽车行业提出了重点扶持新能源汽车的政策,为新能源汽车行业的发展开辟了广阔的前景.某新能源汽车配件公司为扩大生产,计划改进技术生产某种组件,已知生产该组件的年固定成本为 $2000$ 万元,每生产 $x(x \in \mathbf{N}^{*})$万件需另投入成本 $G(x)$万元,且当 $0 < x < 30$ 时,$G(x) = 10x^{2} + 1600x$;当 $x \geq 30$ 时,$G(x) = 2020x + \frac{32000}{x - 10} - 6000$,由市场调研知,该组件每件的售价为 $2000$ 元,且全年内生产的该组件当年能全部销售完.
(1)求年利润 $y$ (万元)与年产量 $x$ (万件)的关系式(利润 $=$ 销售收入 $ -$ 成本);
(2)当该组件的年产量为多少万件时,公司所获年利润最大?最大年利润是多少?
(1)求年利润 $y$ (万元)与年产量 $x$ (万件)的关系式(利润 $=$ 销售收入 $ -$ 成本);
(2)当该组件的年产量为多少万件时,公司所获年利润最大?最大年利润是多少?
答案:
12.解析
(1)由题意可知$y = 2000x - G(x) - 2000$,
当$0<x<30,x\in\mathbf{N}^*$时,$y = 2000x - (10x^2 + 1600x) -2000=-10x^2 + 400x - 2000$;
当$x\geq30,x\in\mathbf{N}^*$时,$y = 2000x - \left(2020x + \frac{32000}{x - 10} -6000\right) - 2000 = 4000 - 20x - \frac{32000}{x - 10}$,
所以年利润$y$(万元)与年产量$x$(万件)的关系式为$y =\begin{cases}-10x^2 + 400x - 2000,0<x<30,\\4000 - 20x - \frac{32000}{x - 10},x\geq30,\end{cases}x\in\mathbf{N}^*$
$\rightarrow$注意自变量的取值范围的限制
(2)当$0<x<30,x\in\mathbf{N}^*$时,$y = -10x^2 + 400x - 2000 =-10(x - 20)^2 + 2000$,
所以当$x = 20$时,$y_{\max}=2000$;
当$x\geq30,x\in\mathbf{N}^*$时,$y = 4000 - 20x - \frac{32000}{x - 10} = 3800 -2\left[20(x - 10) + \frac{32000}{x - 10}\right]\leq3800 - 2\sqrt{20(x - 10)×\frac{32000}{x - 10}} =2200$,当且仅当$20(x - 10)=\frac{32000}{x - 10}$,即$x = 50$时,等号成
立,此时$y_{\max}=2200$.
因为$2000<2200$,所以该组件的年产量为$50$万件时,公
司所获年利润最大,最大年利润为$2200$万元.
(1)由题意可知$y = 2000x - G(x) - 2000$,
当$0<x<30,x\in\mathbf{N}^*$时,$y = 2000x - (10x^2 + 1600x) -2000=-10x^2 + 400x - 2000$;
当$x\geq30,x\in\mathbf{N}^*$时,$y = 2000x - \left(2020x + \frac{32000}{x - 10} -6000\right) - 2000 = 4000 - 20x - \frac{32000}{x - 10}$,
所以年利润$y$(万元)与年产量$x$(万件)的关系式为$y =\begin{cases}-10x^2 + 400x - 2000,0<x<30,\\4000 - 20x - \frac{32000}{x - 10},x\geq30,\end{cases}x\in\mathbf{N}^*$
$\rightarrow$注意自变量的取值范围的限制
(2)当$0<x<30,x\in\mathbf{N}^*$时,$y = -10x^2 + 400x - 2000 =-10(x - 20)^2 + 2000$,
所以当$x = 20$时,$y_{\max}=2000$;
当$x\geq30,x\in\mathbf{N}^*$时,$y = 4000 - 20x - \frac{32000}{x - 10} = 3800 -2\left[20(x - 10) + \frac{32000}{x - 10}\right]\leq3800 - 2\sqrt{20(x - 10)×\frac{32000}{x - 10}} =2200$,当且仅当$20(x - 10)=\frac{32000}{x - 10}$,即$x = 50$时,等号成
立,此时$y_{\max}=2200$.
因为$2000<2200$,所以该组件的年产量为$50$万件时,公
司所获年利润最大,最大年利润为$2200$万元.
查看更多完整答案,请扫码查看


