2025年周末C计划高中数学必修第一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年周末C计划高中数学必修第一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
10. (2025 北京昌平期末)已知函数 $ f(x)=\begin{cases}ax - 2,x < a,\\3x - x^{2},x\geq a.\end{cases} $ 若 $ f(x) $ 无最大值,则实数 $ a $ 的一个取值为
$-1$
;若 $ f(x) $ 存在最大值,则 $ a $ 的取值范围是$[0, 2]$
。
答案:
10.答案 $-1$(答案不唯一,满足$a < 0$即可);$[0, 2]$
解析 当$x < a$时,$f(x) = ax - 2$,当$a < 0$时,$f(x)$单调递减,此时不存在最大值,因此只需满足$a < 0$即可,可取$a = -1$. 若$f(x)$存在最大值,则$a \geq 0$, 当$0 \leq a \leq \frac{3}{2}$时,$y = 3x - x^2$,$x \geq a$的最大值为$\frac{9}{4}$,而$y = ax - 2$,$x < a$单调递增,需满足$a^2 - 2 \leq \frac{9}{4}$,解得$-\frac{\sqrt{17}}{2} \leq a \leq \frac{\sqrt{17}}{2}$,所以$0 \leq a \leq \frac{3}{2}$; 当$a > \frac{3}{2}$时,$y = 3x - x^2$,$x \geq a$的最大值为$3a - a^2$,而$y = ax - 2$,$x < a$单调递增,需满足$a^2 - 2 \leq 3a - a^2$,解得$-\frac{1}{2} \leq a \leq 2$,所以$\frac{3}{2} < a \leq 2$. 综上可得,$a$的取值范围是$[0, 2]$.
解析 当$x < a$时,$f(x) = ax - 2$,当$a < 0$时,$f(x)$单调递减,此时不存在最大值,因此只需满足$a < 0$即可,可取$a = -1$. 若$f(x)$存在最大值,则$a \geq 0$, 当$0 \leq a \leq \frac{3}{2}$时,$y = 3x - x^2$,$x \geq a$的最大值为$\frac{9}{4}$,而$y = ax - 2$,$x < a$单调递增,需满足$a^2 - 2 \leq \frac{9}{4}$,解得$-\frac{\sqrt{17}}{2} \leq a \leq \frac{\sqrt{17}}{2}$,所以$0 \leq a \leq \frac{3}{2}$; 当$a > \frac{3}{2}$时,$y = 3x - x^2$,$x \geq a$的最大值为$3a - a^2$,而$y = ax - 2$,$x < a$单调递增,需满足$a^2 - 2 \leq 3a - a^2$,解得$-\frac{1}{2} \leq a \leq 2$,所以$\frac{3}{2} < a \leq 2$. 综上可得,$a$的取值范围是$[0, 2]$.
11. (2025 湖南长沙长郡中学期中)已知函数 $ f(x) $, $ g(x) $ 是定义在 $ \mathbf{R} $ 上的函数,其中 $ f(x) $ 是奇函数, $ g(x) $ 是偶函数,且 $ f(x)+g(x)=ax^{2}+x + 2 $,若对于任意 $ x_{1},x_{2}\in(1,2) $,且 $ x_{1}<x_{2} $,都有 $ \frac{g(x_{1})-g(x_{2})}{x_{1}-x_{2}}<-1 $,则实数 $ a $ 的取值范围是______
$(-\infty, -\frac{1}{2}]$
。
答案:
11.答案 $(-\infty, -\frac{1}{2}]$
解析 因为$f(x)$是奇函数,$g(x)$是偶函数,所以$f(-x) = -f(x)$,$g(-x) = g(x)$, 对于$f(x) + g(x) = ax^2 + x + 2$用$-x$替换$x$,整理得$f(x) - g(x) = -ax^2 + x - 2$ 联立,解得$f(x) = x$,$g(x) = ax^2 + 2$. 对于任意$x_1, x_2 \in (1, 2)$,且$x_1 < x_2$,$g(x_1) - g(x_2) = x_1 - x_2$等价于$g(x_1) - g(x_2) > x_2 - x_1$,即$g(x_1) + x_1 > g(x_2) + x_2$在$1 < x_1 < x_2 < 2$时恒成立. 记$h(x) = g(x) + x$,则$h(x_1) > h(x_2)$, 即$h(x) = g(x) + x = ax^2 + x + 2$在区间$(1, 2)$上单调递减,
显然$a \neq 0$,$h(x) = ax^2 + x + 2$的图象的对称轴为直线$x = -\frac{1}{2a}$ 当$a > 0$时,$-\frac{1}{2a} < 0$,显然不符合题意; 当$a < 0$时,需使$-\frac{1}{2a} \leq 1$,所以$a \leq -\frac{1}{2}$. 综上可得,实数$a$的取值范围是$(-\infty, -\frac{1}{2}]$.
解析 因为$f(x)$是奇函数,$g(x)$是偶函数,所以$f(-x) = -f(x)$,$g(-x) = g(x)$, 对于$f(x) + g(x) = ax^2 + x + 2$用$-x$替换$x$,整理得$f(x) - g(x) = -ax^2 + x - 2$ 联立,解得$f(x) = x$,$g(x) = ax^2 + 2$. 对于任意$x_1, x_2 \in (1, 2)$,且$x_1 < x_2$,$g(x_1) - g(x_2) = x_1 - x_2$等价于$g(x_1) - g(x_2) > x_2 - x_1$,即$g(x_1) + x_1 > g(x_2) + x_2$在$1 < x_1 < x_2 < 2$时恒成立. 记$h(x) = g(x) + x$,则$h(x_1) > h(x_2)$, 即$h(x) = g(x) + x = ax^2 + x + 2$在区间$(1, 2)$上单调递减,
显然$a \neq 0$,$h(x) = ax^2 + x + 2$的图象的对称轴为直线$x = -\frac{1}{2a}$ 当$a > 0$时,$-\frac{1}{2a} < 0$,显然不符合题意; 当$a < 0$时,需使$-\frac{1}{2a} \leq 1$,所以$a \leq -\frac{1}{2}$. 综上可得,实数$a$的取值范围是$(-\infty, -\frac{1}{2}]$.
12. (13 分)(2025 浙江金华期中)已知 $ f(x)=\begin{cases}-x^{2}+2x,x > 0,\\0,x = 0,\\x^{2}+mx,x < 0\end{cases} $ 是奇函数。
(1)求实数 $ m $ 的值;
(2)作出 $ y = f(x) $ 的图象;
(3)若函数 $ f(x) $ 在区间 $[-1,a - 2]$ 上单调递增,求实数 $ a $ 的取值范围。
(1)求实数 $ m $ 的值;
(2)作出 $ y = f(x) $ 的图象;
(3)若函数 $ f(x) $ 在区间 $[-1,a - 2]$ 上单调递增,求实数 $ a $ 的取值范围。
答案:
12.解析
(1)当$x < 0$时,$-x > 0$,则$f(-x) = -x^2 - 2x$,因为$f(x)$是奇函数,所以$f(x) = -f(-x) = x^2 + 2x$,$x < 0$,所以$m = 2$.
(2)$f(x) = \begin{cases} -x^2 + 2x, & x > 0, \\ 0, & x = 0, \\ x^2 + 2x, & x < 0, \end{cases}$其图象如图所示:
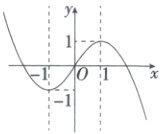
(8分)
(3)由
(2)中图象知,函数$f(x)$的单调递增区间为$[-1, 1]$, (10分) 要使$f(x)$在区间$[-1, a - 2]$上单调递增,则$-1 < a - 2 \leq 1$,解得$1 < a \leq 3$,所以实数$a$的取值范围是$(1, 3]$. (13分)
12.解析
(1)当$x < 0$时,$-x > 0$,则$f(-x) = -x^2 - 2x$,因为$f(x)$是奇函数,所以$f(x) = -f(-x) = x^2 + 2x$,$x < 0$,所以$m = 2$.
(2)$f(x) = \begin{cases} -x^2 + 2x, & x > 0, \\ 0, & x = 0, \\ x^2 + 2x, & x < 0, \end{cases}$其图象如图所示:

(8分)
(3)由
(2)中图象知,函数$f(x)$的单调递增区间为$[-1, 1]$, (10分) 要使$f(x)$在区间$[-1, a - 2]$上单调递增,则$-1 < a - 2 \leq 1$,解得$1 < a \leq 3$,所以实数$a$的取值范围是$(1, 3]$. (13分)
13. (17 分)(2025 河北廊坊期末)我们知道,函数 $ y = f(x) $ 的图象关于坐标原点成中心对称图形的充要条件是函数 $ y = f(x) $ 为奇函数,有同学发现可以将其推广为:函数 $ y = f(x) $ 的图象关于点 $ P(m,n) $ 成中心对称图形的充要条件是函数 $ y = f(x + m)-n $ 为奇函数。已知定义在 $ \mathbf{R} $ 上的函数 $ y = f(x) $ 的图象关于点 $ (1,1) $ 对称。
(1)求 $ f(-1)+f(3) $ 的值;
(2)设函数 $ g(x)=x-\frac{6}{x + 1} $。
①证明函数 $ g(x) $ 的图象关于点 $ (-1,-1) $ 对称;
②用定义证明 $ g(x) $ 在区间 $ (-1,+\infty) $ 上单调递增,并求 $ g(x) $ 在 $[2,+\infty)$ 上的值域;
③当 $ x\in[0,1] $ 时, $ f(x)=x^{2}-2ax + 2a $,若对任意 $ x_{1}\in[0,2] $,总存在 $ x_{2}\in[2,+\infty) $,使得 $ f(x_{1})=g(x_{2}) $ 成立,求实数 $ a $ 的取值范围。
(1)求 $ f(-1)+f(3) $ 的值;
(2)设函数 $ g(x)=x-\frac{6}{x + 1} $。
①证明函数 $ g(x) $ 的图象关于点 $ (-1,-1) $ 对称;
②用定义证明 $ g(x) $ 在区间 $ (-1,+\infty) $ 上单调递增,并求 $ g(x) $ 在 $[2,+\infty)$ 上的值域;
③当 $ x\in[0,1] $ 时, $ f(x)=x^{2}-2ax + 2a $,若对任意 $ x_{1}\in[0,2] $,总存在 $ x_{2}\in[2,+\infty) $,使得 $ f(x_{1})=g(x_{2}) $ 成立,求实数 $ a $ 的取值范围。
答案:
13.解析 若函数$y = f(x + m) - n$为奇函数,则$f(-x + m) - n + f(x + m) - n = 0$,即$f(x + m) + f(-x + m) = 2n$. (1分)
(1)因为$y = f(x)$的图象关于点$(1, 1)$对称,所以$f(x + 1) + f(1 - x) = 2$,令$x = 2$,得$f(-1) + f(3) = 2$. (3分)
(2)①证明:函数$g(x) = x - \frac{6}{x + 1}$的定义域为$\{x \mid x \neq -1\}$, 因为$g(-1 + x) + g(-1 - x) = -1 + x - \frac{6}{-1 + x + 1} - 1 - x - \frac{6}{-1 - x + 1} = -2 - \frac{6}{x} - \frac{6}{-x} = -2 - \frac{6}{x} + \frac{6}{x} = -2$, 所以$g(x)$的图象的对称中心为$(-1, -1)$. (5分)
②任取$x_1, x_2 \in (-1, +\infty)$,且$x_1 < x_2$,则$g(x_1) - g(x_2) = x_1 - \frac{6}{x_1 + 1} - (x_2 - \frac{6}{x_2 + 1}) = (x_1 - x_2) \left[ 1 + \frac{6}{(x_1 + 1)(x_2 + 1)} \right]$, 因为$-1 < x_1 < x_2$,所以$x_1 - x_2 < 0$,$1 + \frac{6}{(x_1 + 1)(x_2 + 1)} > 0$,所以$g(x_1) - g(x_2) < 0$,即$g(x_1) < g(x_2)$,所以$g(x) = x - \frac{6}{x + 1}$在$(-1, +\infty)$上单调递增. (7分)
所以$g(x)$在$[2, +\infty)$上单调递增,又$g(2) = 2 - \frac{6}{2 + 1} = 0$,所以$g(x)$在$[2, +\infty)$上的值域为$[0, +\infty)$. (9分)
③因为对任意$x_1 \in [0, 2]$,总存在$x_2 \in [2, +\infty)$,使得$f(x_1) = g(x_2)$成立,所以$f(x)$在$[0, 2]$上的值域是$g(x)$在$[2, +\infty)$上的值域的子集,记$f(x)$在$[0, 2]$上的值域为$B$,则$B \subseteq [0, +\infty)$. 当$x \in [0, 1]$时,$f(x) = x^2 - 2ax + 2a$, 若$a \leq 0$,则$f(x)$在$[0, 1]$上单调递增,因为$y = f(x)$的图象关于点$(1, 1)$对称,所以$f(x)$在$[1, 2]$上单调递增,所以$f(x)$在$[0, 2]$上单调递增, 故只需$f(0) = 2a \geq 0$即可,解得$a \geq 0$,所以$a = 0$满足题意; (12分)
当$0 < a < 1$时,$f(x)$在$[0, a]$上单调递减,在$[a, 1]$上单调递增,因为$y = f(x)$的图象关于点$(1, 1)$对称,所以$f(x)$在$[1, 2 - a]$上单调递增,在$[2 - a, 2]$上单调递减, 所以$B = [f(a), f(2 - a)]$或$B = [f(2), f(0)]$,当$0 < a < 1$时,$f(a) = -a^2 + 2a > 0$,$f(2) = 2 - f(0) = 2 - 2a > 0$,所以$0 < a < 1$满足题意; (14分)
当$a \geq 1$时,$f(x)$在$[0, 1]$上单调递减,因为$y = f(x)$的图象关于点$(1, 1)$对称,所以$f(x)$在$[1, 2]$上单调递减,故只需$f(2) = 2 - 2a \geq 0$即可,解得$a \leq 1$,所以$a = 1$满足题意. (16分)
综上所述,实数$a$的取值范围为$[0, 1]$. (17分)
(1)因为$y = f(x)$的图象关于点$(1, 1)$对称,所以$f(x + 1) + f(1 - x) = 2$,令$x = 2$,得$f(-1) + f(3) = 2$. (3分)
(2)①证明:函数$g(x) = x - \frac{6}{x + 1}$的定义域为$\{x \mid x \neq -1\}$, 因为$g(-1 + x) + g(-1 - x) = -1 + x - \frac{6}{-1 + x + 1} - 1 - x - \frac{6}{-1 - x + 1} = -2 - \frac{6}{x} - \frac{6}{-x} = -2 - \frac{6}{x} + \frac{6}{x} = -2$, 所以$g(x)$的图象的对称中心为$(-1, -1)$. (5分)
②任取$x_1, x_2 \in (-1, +\infty)$,且$x_1 < x_2$,则$g(x_1) - g(x_2) = x_1 - \frac{6}{x_1 + 1} - (x_2 - \frac{6}{x_2 + 1}) = (x_1 - x_2) \left[ 1 + \frac{6}{(x_1 + 1)(x_2 + 1)} \right]$, 因为$-1 < x_1 < x_2$,所以$x_1 - x_2 < 0$,$1 + \frac{6}{(x_1 + 1)(x_2 + 1)} > 0$,所以$g(x_1) - g(x_2) < 0$,即$g(x_1) < g(x_2)$,所以$g(x) = x - \frac{6}{x + 1}$在$(-1, +\infty)$上单调递增. (7分)
所以$g(x)$在$[2, +\infty)$上单调递增,又$g(2) = 2 - \frac{6}{2 + 1} = 0$,所以$g(x)$在$[2, +\infty)$上的值域为$[0, +\infty)$. (9分)
③因为对任意$x_1 \in [0, 2]$,总存在$x_2 \in [2, +\infty)$,使得$f(x_1) = g(x_2)$成立,所以$f(x)$在$[0, 2]$上的值域是$g(x)$在$[2, +\infty)$上的值域的子集,记$f(x)$在$[0, 2]$上的值域为$B$,则$B \subseteq [0, +\infty)$. 当$x \in [0, 1]$时,$f(x) = x^2 - 2ax + 2a$, 若$a \leq 0$,则$f(x)$在$[0, 1]$上单调递增,因为$y = f(x)$的图象关于点$(1, 1)$对称,所以$f(x)$在$[1, 2]$上单调递增,所以$f(x)$在$[0, 2]$上单调递增, 故只需$f(0) = 2a \geq 0$即可,解得$a \geq 0$,所以$a = 0$满足题意; (12分)
当$0 < a < 1$时,$f(x)$在$[0, a]$上单调递减,在$[a, 1]$上单调递增,因为$y = f(x)$的图象关于点$(1, 1)$对称,所以$f(x)$在$[1, 2 - a]$上单调递增,在$[2 - a, 2]$上单调递减, 所以$B = [f(a), f(2 - a)]$或$B = [f(2), f(0)]$,当$0 < a < 1$时,$f(a) = -a^2 + 2a > 0$,$f(2) = 2 - f(0) = 2 - 2a > 0$,所以$0 < a < 1$满足题意; (14分)
当$a \geq 1$时,$f(x)$在$[0, 1]$上单调递减,因为$y = f(x)$的图象关于点$(1, 1)$对称,所以$f(x)$在$[1, 2]$上单调递减,故只需$f(2) = 2 - 2a \geq 0$即可,解得$a \leq 1$,所以$a = 1$满足题意. (16分)
综上所述,实数$a$的取值范围为$[0, 1]$. (17分)
查看更多完整答案,请扫码查看


