《2025年周末C计划高中数学必修第一册人教版》

11. (2025 安徽阜阳阜南实验中学月考)已知函数$f(x)=\lg(\sqrt{x^{2}-2x + 2}-x + 1)$，则下列说法正确的是（ABD）
A.$f(x)$的值域为$\mathbf{R}$
B.$f(x + 1)$的图象关于原点对称
C.$f(x)$在$(1,+\infty)$上单调递增
D.若$f(x)$在$x\in[1 - m,1 + m]$上的最大值、最小值分别为$M$，$N$，则$M + N = 0$

答案： 11.ABD 对于A，$x^{2} - 2x + 2 - (x - 1)^{2} = 1 ＞ 0$，所以$\sqrt{x^{2} - 2x + 2} ＞ (x - 1)^{2} \geq 0$，则$\sqrt{x^{2} - 2x + 2} - x + 1 ＞ 0$恒成立，所以$f(x)$的定义域为$\mathbf{R}$，
又当$x \to + \infty$时，$y = \sqrt{x^{2} - 2x + 2} - x + 1 = \frac{1}{\sqrt{x^{2} - 2x + 2} + x - 1} \to 0$，$\lg y \to - \infty$，
当$x \to - \infty$时，$y = \sqrt{x^{2} - 2x + 2} - x + 1 \to + \infty$，$\lg y \to + \infty$，且$f(1) = 0$，$f(x)$的图象连续不断，所以$f(x)$的值域为$\mathbf{R}$，故A正确；
对于B，$f(x + 1) = \lg(\sqrt{(x + 1)^{2} - 2(x + 1) + 2} - (x + 1) + 1) = \lg(\sqrt{x^{2} + 1} - x)$，
令$k(x) = f(x + 1) = \lg(\sqrt{x^{2} + 1} - x)$，易知$k(x)$的定义域为$\mathbf{R}$，
又$k( - x) + k(x) = \lg(\sqrt{x^{2} + 1} + x) + \lg(\sqrt{x^{2} + 1} - x) = \lg 1 = 0$，所以$k(x)$为奇函数，其图象关于原点对称，即$f(x + 1)$的图象关于原点对称，故B正确；
对于C，由B知$k(x) = \lg(\sqrt{x^{2} + 1} - x) = \lg\frac{1}{\sqrt{x^{2} + 1} + x}$，易知其在$\mathbf{R}$上单调递减，
又$k(x) = f(x + 1)$，所以将$k(x)$的图象向右平移一个单位长度可得$f(x)$的图象，所以$f(x)$在$\mathbf{R}$上单调递减，故C错误；
对于D，由C知$f(x)$在$\mathbf{R}$上单调递减，故$f(x)$在$[1 - m,1 + m]$上单调递减，
则$M = f(1 - m)$，$N = f(1 + m)$，故$M + N = f(1 - m) + f(1 + m) = k( - m) + k(m) = 0$，故D正确。

12. (2025 安徽宣城二中月考)一个扇形的弧长和面积都是$\frac{2\pi}{3}$，则这个扇形的半径为2.

答案： 12.答案：2
解析：设扇形的弧长为$l$，半径为$r$，面积为$S$，则$l = \frac{2\pi}{3}$，$S = \frac{1}{2}lr = \frac{1}{2} × \frac{2\pi}{3} × r = \frac{2\pi}{3}$，解得$r = 2$。

13. (2025 湖北武汉调研)为了响应节能减排号召，某地政府决定大规模铺设光伏太阳能板，该地区未来第$x$年年底光伏太阳能板的保有量$y$（单位：万块）满足模型$y=\frac{N}{1+\left(\frac{N}{y_{0}}-1\right)e^{-px}}$，其中$N$为饱和度，$y_{0}$为初始值，$p$为年增长率.若该地区 2024 年年底的光伏太阳能板的保有量约为 20 万块，以此为初始值，以后每年的增长率均为 10%，饱和度为 1020 万块，那么 2030 年年底该地区光伏太阳能板的保有量约为________万块.（结果四舍五入保留整数，参考数据：$e^{-0.5}\approx0.61$，$e^{-0.6}\approx0.55$，$e^{-0.7}\approx0.50$）
36

答案： 13.答案：36
解析：由题意得$y_{0} = 20$，$N = 1020$，$p = 10\% = 0.1$，$x = 6$，
则2030年年底该地区光伏太阳能板的保有量为$\frac{1020}{1 + (\frac{1020}{20} - 1)e^{- 0.1 × 6}} = \frac{1020}{1 + 50e^{- 0.6}}$，
因为$e^{- 0.6} \approx 0.55$，所以$\frac{1020}{1 + 50e^{- 0.6}} \approx \frac{1020}{1 + 50 × 0.55} \approx 36$，
所以2030年年底该地区光伏太阳能板的保有量约为36万块。

14. 创新题 新考法 (2025 云南联考)对于任意实数$a$，$b$，定义符号$\max\{a,b\}$，当$a\geq b$时，$\max\{a,b\}=a$；当$a\lt b$时，$\max\{a,b\}=b$.若$f(x)=1 - x^{2}$，$g(x)=\log_{2}|x|$，函数$F(x)=\max\{f(x),g(x)\}-k$有$4$个零点，则$k$的取值范围为________.

答案：
14.答案：$(0,1)$
解析：在同一坐标系内作出$f(x)$，$g(x)$的图象，如图1所示，

则$\max\{ f(x),g(x)\} = \begin{cases} \log_{2}( - x),x ＜ - 1, \\1 - x^{2}, - 1 \leq x \leq 1, \\\log_{2}x,x ＞ 1, \end{cases}$如图2，

令$F(x) = 0$，则$k = \max\{ f(x),g(x)\}$，
故若$F(x)$有4个零点，则$y = \max\{ f(x),g(x)\}$的图象与直线$y = k$有4个交点，由图2可得$0 ＜ k ＜ 1$，
故$k$的取值范围为$(0,1)$。

15. (13 分)(2025 浙江宁波期末)如图，单位圆$O$与$x$轴正半轴的交点为$A$，点$B$，$C$在圆$O$上，且点$B$在第一象限内，点$C$在第二象限内.

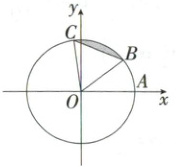
(1)当$\overgroup{BC}$的长为$\frac{\pi}{3}$时，求线段$BC$与$\overgroup{BC}$所围成的弓形（阴影部分）面积；
(2)记$\angle AOC=\alpha,\alpha\in\left(\frac{\pi}{2},\pi\right)$，当$BO\perp CO$，点$B$的横坐标为$\frac{4}{5}$时，求$\sin\alpha+\cos\alpha$的值.

答案： 15.解析：
(1)设$BC$所对的圆心角为$\theta$，$BC$长为$l$，弓形的面积为$S$。
因为$l = \frac{\pi}{3}$，圆$O$的半径$r = 1$，所以$\theta = \frac{l}{r} = \frac{\pi}{3}$，(3分)
故$S_{扇形BOC} = \frac{1}{2}\theta r^{2} = \frac{1}{2} × \frac{\pi}{3} × 1^{2} = \frac{\pi}{6}$，易知$\triangle BOC$为等边三角形，所以$S_{\triangle BOC} = \frac{1}{2} × 1 × \sqrt{1 - (\frac{1}{2})^{2}} = \frac{\sqrt{3}}{4}$，
故$S = S_{扇形BOC} - S_{\triangle BOC} = \frac{\pi}{6} - \frac{\sqrt{3}}{4}$。(6分)
(2)设$\angle AOB = \beta$，则$\alpha = 90^{\circ} + \beta$，由题知$B(\frac{4}{5},\frac{3}{5})$，则$\sin\beta = \frac{3}{5}$，$\cos\beta = \frac{4}{5}$，(9分)
所以$\sin\alpha + \cos\alpha = \sin(90^{\circ} + \beta) + \cos(90^{\circ} + \beta) = \cos\beta - \sin\beta = \frac{4}{5} - \frac{3}{5} = \frac{1}{5}$。(13分)

16. (15 分)(2025 福建部分学校期中)已知$\sin\theta$和$\cos\theta$是关于$x$的方程$x^{2}+mx+\frac{1}{2}=0$的两实根，且$0\lt\theta\lt\frac{\pi}{2}$.
(1)求$m$的值；
(2)求$\sin^{4}\theta+\cos^{4}\theta$的值；
(3)求$\frac{\tan\theta+\tan\frac{7\pi}{3}}{1-\tan\theta\tan\frac{4\pi}{3}}$的值.

答案： 16.解析：
(1)因为$\sin\theta$和$\cos\theta$是关于$x$的方程$x^{2} + mx + \frac{1}{2} = 0$的两实根，
所以$\Delta = m^{2} - 2 \geq 0$，$\sin\theta + \cos\theta = - m$①，$\sin\theta\cos\theta = \frac{1}{2}$②，则$m \geq \sqrt{2}$或$m \leq - \sqrt{2}$，(2分)
将①式等号两边平方可得$(\sin\theta + \cos\theta)^{2} = m^{2}$，
即$\sin^{2}\theta + 2\sin\theta\cos\theta + \cos^{2}\theta = m^{2}$，即$\sin\theta\cos\theta = \frac{m^{2} - 1}{2}$，
结合②式得$m^{2} = 2$，解得$m = \pm \sqrt{2}$。(4分)
因为$0 ＜ \theta ＜ \frac{\pi}{2}$，所以$\sin\theta ＞ 0$，$\cos\theta ＞ 0$，
则$\sin\theta + \cos\theta = - m ＞ 0$，则$m ＜ 0$，故$m = - \sqrt{2}$。(5分)
(2)因为$\sin\theta\cos\theta = \frac{1}{2}$，
所以$\sin^{4}\theta + \cos^{4}\theta = (\sin^{2}\theta + \cos^{2}\theta)^{2} - 2\sin^{2}\theta\cos^{2}\theta = 1 - 2 × (\frac{1}{2})^{2} = \frac{1}{2}$。(8分)
(3)由
(1)知$\cos\theta = \sqrt{2} - \sin\theta$，将其代入$\sin\theta\cos\theta = \frac{1}{2}$，
得$\sin\theta(\sqrt{2} - \sin\theta) = \frac{1}{2}$，
整理得$\sin^{2}\theta - \sqrt{2}\sin\theta + \frac{1}{2} = 0$，所以$\sin\theta = \frac{\sqrt{2}}{2}$，故$\cos\theta = \sqrt{2} - \frac{\sqrt{2}}{2} = \frac{\sqrt{2}}{2}$，
所以$\tan\theta = \frac{\sin\theta}{\cos\theta} = \frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = 1$。(12分)
$\frac{\tan\theta + \tan\frac{7\pi}{3}}{1 - \tan\theta\tan\frac{4\pi}{3}} = \frac{\tan\theta + \tan\frac{\pi}{3}}{1 - \tan\theta\tan\frac{\pi}{3}} = \frac{1 + \sqrt{3}}{1 - 1 × \sqrt{3}} = \frac{1 + \sqrt{3}}{1 - \sqrt{3}} = - 2 - \sqrt{3}$。(15分)