2025年周末C计划高中数学必修第一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年周末C计划高中数学必修第一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. (2025重庆巴蜀中学月考)已知$2^{x}=3^{y}=5^{z}(x,y,z\neq0)$,且$\frac{1}{x}+\frac{1}{y}=\frac{a}{z}$,则$a=$(
A.$\log_{2}3$
B.$\log_{2}5$
C.$\log_{3}5$
D.$\log_{5}6$
D
)A.$\log_{2}3$
B.$\log_{2}5$
C.$\log_{3}5$
D.$\log_{5}6$
答案:
1.D 设$2^{x}=3^{y}=5^{z}=k(k>0),$则$x=log_{2}k,$$y=log_{3}k,$$z =log_{5}k。$
因为$\frac{1}{x}+\frac{1}{y}=\frac{a}{z},$所以$\frac{1}{log_{2}k}+\frac{1}{log_{3}k}=log_{k}2+log_{k}3=log_{k}6=a log_{k}5,$所以$5^{a}=6,$解得$a=log_{5}6。$
因为$\frac{1}{x}+\frac{1}{y}=\frac{a}{z},$所以$\frac{1}{log_{2}k}+\frac{1}{log_{3}k}=log_{k}2+log_{k}3=log_{k}6=a log_{k}5,$所以$5^{a}=6,$解得$a=log_{5}6。$
2. (2023全国甲文,11)已知函数$f(x)=e^{-(x - 1)^{2}}$.记$a = f(\frac{\sqrt{2}}{2})$,$b = f(\frac{\sqrt{3}}{2})$,$c = f(\frac{\sqrt{6}}{2})$,则(
A.$b > c > a$
B.$b > a > c$
C.$c > b > a$
D.$c > a > b$
A
)A.$b > c > a$
B.$b > a > c$
C.$c > b > a$
D.$c > a > b$
答案:
2.A 令$g(x)=−(x−1)^{2},$则g(x)的图象开口向下,对称轴方程为x=1,g(x)在(−∞,1)上单调递增,在(1,+∞)上单调递减。
因为$\frac{\sqrt{2}}{2}<\frac{\sqrt{3}}{2}<1<\frac{\sqrt{6}}{2},$所以$g(\frac{\sqrt{2}}{2})<g(\frac{\sqrt{3}}{2})。$
接下来比较$g(\frac{\sqrt{2}}{2}),$$g(\frac{\sqrt{3}}{2})$与$g(\frac{\sqrt{6}}{2})$的大小,即比较$1−\frac{\sqrt{2}}{2},$$1−\frac{\sqrt{3}}{2}$与$\frac{\sqrt{6}}{2}−1$的大小。
易知$\frac{\sqrt{6}}{2}−1-(1−\frac{\sqrt{3}}{2})=\frac{\sqrt{6}+\sqrt{3}}{2}-\frac{4}{2},$而$(\sqrt{6}+\sqrt{3})^{2}-4^{2}=9+6\sqrt{2}-16=6\sqrt{2}-7>0,$
所以$\frac{\sqrt{6}}{2}−1-(1−\frac{\sqrt{3}}{2})=\frac{\sqrt{6}+\sqrt{3}}{2}-\frac{4}{2}>0,$即$\frac{\sqrt{6}}{2}−1>1−\frac{\sqrt{3}}{2},$所以$g(\frac{\sqrt{6}}{2})<g(\frac{\sqrt{3}}{2})。$
易知$\frac{\sqrt{6}}{2}−1-(1−\frac{\sqrt{2}}{2})=\frac{\sqrt{6}+\sqrt{2}}{2}-\frac{4}{2},$而$(\sqrt{6}+\sqrt{2})^{2}-4^{2}=8+4\sqrt{3}-16=4\sqrt{3}-8=4(\sqrt{3}-2)<0,$即$\frac{\sqrt{6}}{2}−1<1−\frac{\sqrt{2}}{2},$所以$g(\frac{\sqrt{6}}{2})>g(\frac{\sqrt{2}}{2})。$
综上,$g(\frac{\sqrt{2}}{2})<g(\frac{\sqrt{6}}{2})<g(\frac{\sqrt{3}}{2})。$
又$y=e^{x}$为增函数,所以$e^{g(\frac{\sqrt{2}}{2})}<e^{g(\frac{\sqrt{6}}{2})}<e^{g(\frac{\sqrt{3}}{2})},$即a<c<b。
因为$\frac{\sqrt{2}}{2}<\frac{\sqrt{3}}{2}<1<\frac{\sqrt{6}}{2},$所以$g(\frac{\sqrt{2}}{2})<g(\frac{\sqrt{3}}{2})。$
接下来比较$g(\frac{\sqrt{2}}{2}),$$g(\frac{\sqrt{3}}{2})$与$g(\frac{\sqrt{6}}{2})$的大小,即比较$1−\frac{\sqrt{2}}{2},$$1−\frac{\sqrt{3}}{2}$与$\frac{\sqrt{6}}{2}−1$的大小。
易知$\frac{\sqrt{6}}{2}−1-(1−\frac{\sqrt{3}}{2})=\frac{\sqrt{6}+\sqrt{3}}{2}-\frac{4}{2},$而$(\sqrt{6}+\sqrt{3})^{2}-4^{2}=9+6\sqrt{2}-16=6\sqrt{2}-7>0,$
所以$\frac{\sqrt{6}}{2}−1-(1−\frac{\sqrt{3}}{2})=\frac{\sqrt{6}+\sqrt{3}}{2}-\frac{4}{2}>0,$即$\frac{\sqrt{6}}{2}−1>1−\frac{\sqrt{3}}{2},$所以$g(\frac{\sqrt{6}}{2})<g(\frac{\sqrt{3}}{2})。$
易知$\frac{\sqrt{6}}{2}−1-(1−\frac{\sqrt{2}}{2})=\frac{\sqrt{6}+\sqrt{2}}{2}-\frac{4}{2},$而$(\sqrt{6}+\sqrt{2})^{2}-4^{2}=8+4\sqrt{3}-16=4\sqrt{3}-8=4(\sqrt{3}-2)<0,$即$\frac{\sqrt{6}}{2}−1<1−\frac{\sqrt{2}}{2},$所以$g(\frac{\sqrt{6}}{2})>g(\frac{\sqrt{2}}{2})。$
综上,$g(\frac{\sqrt{2}}{2})<g(\frac{\sqrt{6}}{2})<g(\frac{\sqrt{3}}{2})。$
又$y=e^{x}$为增函数,所以$e^{g(\frac{\sqrt{2}}{2})}<e^{g(\frac{\sqrt{6}}{2})}<e^{g(\frac{\sqrt{3}}{2})},$即a<c<b。
3. (2025湖南名校联合体联考)已知函数$f(x)=x^{3}-\frac{2}{e^{x}+1}+3$,且$f(a^{2})+f(3a - 4) > 4$,则实数$a$的取值范围是(
A.$(-\infty,-4)\cup(1,+\infty)$
B.$(-4,1)$
C.$(-\infty,-1)\cup(4,+\infty)$
D.$(-1,4)$
(−∞,−4)∪(1,+∞)
)A.$(-\infty,-4)\cup(1,+\infty)$
B.$(-4,1)$
C.$(-\infty,-1)\cup(4,+\infty)$
D.$(-1,4)$
答案:
$3.A f(x)=x^{3}-\frac{2}{e^{x}+1}+3=x^{3}-\frac{e^{x}+1}{e^{x}+1}+\frac{e^{x}-1}{e^{x}+1}+2=x^{3}+\frac{e^{x}-1}{e^{x}+1}+2。$令$g(x)=x^{3}+\frac{e^{x}-1}{e^{x}+1},$则f(x)=g(x)+2。
由$f(a^{2})+f(3a−4)>4$得$g(a^{2})+2+g(3a−4)+2>4,$所以$g(a^{2})+g(3a−4)>0,$即$g(a^{2})>−g(3a−4)。$
因为g(x)的定义域为R,且$g(−x)=(−x)^{3}+\frac{e^{-x}-1}{e^{-x}+1}=−x^{3}+\frac{1−e^{x}}{1+e^{x}}=−g(x),$
所以g(x)是R上的奇函数,所以−g(3a−4)=g(4−3a)。易知$y=x^{3}$在R上为增函数,$y=\frac{2}{e^{x}+1}$在R上为减函数,所以$g(x)=x^{3}+\frac{e^{x}-1}{e^{x}+1}=x^{3}-\frac{2}{e^{x}+1}+1$在R上为增函数。所以由$g(a^{2})>g(4−3a),$得$a^{2}>4−3a,$解得a>1或a<−4。
所以实数a的取值范围为(−∞,−4)∪(1,+∞)。
由$f(a^{2})+f(3a−4)>4$得$g(a^{2})+2+g(3a−4)+2>4,$所以$g(a^{2})+g(3a−4)>0,$即$g(a^{2})>−g(3a−4)。$
因为g(x)的定义域为R,且$g(−x)=(−x)^{3}+\frac{e^{-x}-1}{e^{-x}+1}=−x^{3}+\frac{1−e^{x}}{1+e^{x}}=−g(x),$
所以g(x)是R上的奇函数,所以−g(3a−4)=g(4−3a)。易知$y=x^{3}$在R上为增函数,$y=\frac{2}{e^{x}+1}$在R上为减函数,所以$g(x)=x^{3}+\frac{e^{x}-1}{e^{x}+1}=x^{3}-\frac{2}{e^{x}+1}+1$在R上为增函数。所以由$g(a^{2})>g(4−3a),$得$a^{2}>4−3a,$解得a>1或a<−4。
所以实数a的取值范围为(−∞,−4)∪(1,+∞)。
4. (2024河北NT20名校联合体月考)已知$a > 1$,$f(x)=\begin{cases}(a - 1)^{x},x\leq\frac{1}{2},\\x+\frac{a}{x}-2,x>\frac{1}{2}\end{cases}$的值域为$D$,$D\subseteq[\frac{2}{3},+\infty)$,则实数$a$的取值范围是(
A.$(1,2)$
B.$(2,3)$
C.$(1,\frac{16}{9}$
D.$[\frac{16}{9},2]$
$[\frac{16}{9},2]$
)A.$(1,2)$
B.$(2,3)$
C.$(1,\frac{16}{9}$
D.$[\frac{16}{9},2]$
答案:
4.D 若1<a<2,则当$x≤\frac{1}{2}$时,$f(x)=(a−1)^{x}$单调递减,此时$f(x)∈[\sqrt{a−1},+∞);$
当$x>\frac{1}{2}$时,$f(x)=x+\frac{a}{x}-2≥2\sqrt{a}-2,$当且仅当$x=\sqrt{a}>\frac{1}{2}$时,等号成立。
又函数f(x)的值域D满足$D⊆[\frac{2}{3},+∞),$所以$\begin{cases}\sqrt{a}-2\geq\frac{2}{3}\\1<a<2\end{cases},$解得$\frac{16}{9}≤a<2。$
若a = 2,则$f(x)=\begin{cases}1,x\leq\frac{1}{2}\\x+\frac{2}{x}-2,x>\frac{1}{2}\end{cases},$故当$x≤\frac{1}{2}$时,f(x)=1;当$x>\frac{1}{2}$时,$f(x)=x+\frac{2}{x}-2≥2\sqrt{2}-2,$当且仅当$x=\sqrt{2}$时,等号成立,所以函数f(x)的值域$D=[2\sqrt{2}-2,+∞),$满足$D⊆[\frac{2}{3},+∞)。$
若a>2,则当$x≤\frac{1}{2}$时,$f(x)=(a−1)^{x}$在$(−∞,\frac{1}{2}]$上单调递增,此时$f(x)∈(0,\sqrt{a−1}],$
所以$(0,\sqrt{a−1}]⊆D,$而$(0,\sqrt{a−1}]⊆[\frac{2}{3},+∞)$不成立,所以a>2不满足题意。
综上,实数a的取值范围为$[\frac{16}{9},2]。$
当$x>\frac{1}{2}$时,$f(x)=x+\frac{a}{x}-2≥2\sqrt{a}-2,$当且仅当$x=\sqrt{a}>\frac{1}{2}$时,等号成立。
又函数f(x)的值域D满足$D⊆[\frac{2}{3},+∞),$所以$\begin{cases}\sqrt{a}-2\geq\frac{2}{3}\\1<a<2\end{cases},$解得$\frac{16}{9}≤a<2。$
若a = 2,则$f(x)=\begin{cases}1,x\leq\frac{1}{2}\\x+\frac{2}{x}-2,x>\frac{1}{2}\end{cases},$故当$x≤\frac{1}{2}$时,f(x)=1;当$x>\frac{1}{2}$时,$f(x)=x+\frac{2}{x}-2≥2\sqrt{2}-2,$当且仅当$x=\sqrt{2}$时,等号成立,所以函数f(x)的值域$D=[2\sqrt{2}-2,+∞),$满足$D⊆[\frac{2}{3},+∞)。$
若a>2,则当$x≤\frac{1}{2}$时,$f(x)=(a−1)^{x}$在$(−∞,\frac{1}{2}]$上单调递增,此时$f(x)∈(0,\sqrt{a−1}],$
所以$(0,\sqrt{a−1}]⊆D,$而$(0,\sqrt{a−1}]⊆[\frac{2}{3},+∞)$不成立,所以a>2不满足题意。
综上,实数a的取值范围为$[\frac{16}{9},2]。$
5. (2025西南名校联盟联考)若不等式$(3^{x + 2a}-9)(x - b)\geq0$在$x\in\mathbf{R}$上恒成立,且$a > 0$,$b > 0$,则$\frac{2}{a}+\frac{1}{b}$的最小值为(
A.$\frac{3}{2}$
B.$\frac{5}{2}$
C.$\frac{7}{2}$
D.$\frac{9}{2}$
$\frac{9}{2}$
)A.$\frac{3}{2}$
B.$\frac{5}{2}$
C.$\frac{7}{2}$
D.$\frac{9}{2}$
答案:
5.D 由$(3^{x + 2a}-9)(x - b)≥0,$得$\begin{cases}3^{x + 2a}-9\geq0\\x - b\geq0\end{cases}$或$\begin{cases}3^{x + 2a}-9\leq0\\x - b\leq0\end{cases},$即$\begin{cases}3^{x + 2a}\geq3^{2}\\x - b\geq0\end{cases}$或$\begin{cases}3^{x + 2a}\leq3^{2}\\x - b\leq0\end{cases}。$
易知$y=3^{x}$为增函数,所以$\begin{cases}x + 2a\geq2\\x\geq b\end{cases}$或$\begin{cases}x + 2a\leq2\\x\leq b\end{cases},$即$\begin{cases}x\geq2 - 2a\\x\geq b\end{cases}$或$\begin{cases}x\leq2 - 2a\\x\leq b\end{cases}。$
当2 - 2a>b时,解得x≤b或x≥2 - 2a,所以存在x∈(b,2 - 2a),使得$(3^{x + 2a}-9)(x - b)<0$成立,与题意不符。
当2 - 2a<b时,解得x≤2 - 2a或x≥b,所以存在x∈(2 - 2a,b),使得$(3^{x + 2a}-9)(x - b)<0$成立,与题意不符。
当2 - 2a = b时,解集为R,即$(3^{x + 2a}-9)(x - b)≥0$在x∈R上恒成立。
所以2 - 2a = b,即2a + b = 2。
因为a>0,b>0,所以$\frac{2}{a}+\frac{1}{b}=\frac{1}{2}(\frac{2}{a}+\frac{1}{b})(2a + b)=\frac{1}{2}(\frac{2a}{b}+\frac{2b}{a}+5)\geq\frac{1}{2}(2\sqrt{\frac{2a}{b}·\frac{2b}{a}}+5)=\frac{9}{2},$当且仅当$\frac{2a}{b}=\frac{2b}{a},$2a + b = 2,即$a = b=\frac{2}{3}$时取等号,所以$\frac{2}{a}+\frac{1}{b}$的最小值为$\frac{9}{2}。$
易知$y=3^{x}$为增函数,所以$\begin{cases}x + 2a\geq2\\x\geq b\end{cases}$或$\begin{cases}x + 2a\leq2\\x\leq b\end{cases},$即$\begin{cases}x\geq2 - 2a\\x\geq b\end{cases}$或$\begin{cases}x\leq2 - 2a\\x\leq b\end{cases}。$
当2 - 2a>b时,解得x≤b或x≥2 - 2a,所以存在x∈(b,2 - 2a),使得$(3^{x + 2a}-9)(x - b)<0$成立,与题意不符。
当2 - 2a<b时,解得x≤2 - 2a或x≥b,所以存在x∈(2 - 2a,b),使得$(3^{x + 2a}-9)(x - b)<0$成立,与题意不符。
当2 - 2a = b时,解集为R,即$(3^{x + 2a}-9)(x - b)≥0$在x∈R上恒成立。
所以2 - 2a = b,即2a + b = 2。
因为a>0,b>0,所以$\frac{2}{a}+\frac{1}{b}=\frac{1}{2}(\frac{2}{a}+\frac{1}{b})(2a + b)=\frac{1}{2}(\frac{2a}{b}+\frac{2b}{a}+5)\geq\frac{1}{2}(2\sqrt{\frac{2a}{b}·\frac{2b}{a}}+5)=\frac{9}{2},$当且仅当$\frac{2a}{b}=\frac{2b}{a},$2a + b = 2,即$a = b=\frac{2}{3}$时取等号,所以$\frac{2}{a}+\frac{1}{b}$的最小值为$\frac{9}{2}。$
6. (2025江苏百校大联考)已知函数$f(x)=\begin{cases}|2^{x}-1|,x\leq2,\\5 - x,x > 2,\end{cases}$若$a < b < c < d$且$f(a)=f(b)=f(d)<f(c)$,则下列说法错误的是( )
A.$a < 0$
B.$c\geq1$
C.$2^{a}d < 5$
D.$2^{a}+2^{b}+2^{d}\in(18,34)$
A.$a < 0$
B.$c\geq1$
C.$2^{a}d < 5$
D.$2^{a}+2^{b}+2^{d}\in(18,34)$
答案:
6.B 作出函数f(x)的图象,如图所示。

作y=|$2^{x}-1$|的图象时,先作$y=2^{x}-1$的图象,再将图象位于x轴下方的部分沿x轴翻折到x轴的上方,其余不变,即可得到y=|$2^{x}-1$|的图象。
因为a<b<c<d且f(a)=f(b)=f(d)<f(c),所以a<0,0<b<1,4<d<5,b<c,但得不出c≥1,故A中说法正确,B中说法错误。
因为f(a)=f(d),所以|$2^{a}-1$|=5 - d,所以$1 - 2^{a}=5 - d,$所以$2^{a}=d - 4,$所以$2^{a}d=d(d - 4)=d^{2}-4d,$易知$y=d^{2}-4d$在(4,5)上单调递增,所以$d^{2}-4d<5,$故C中说法正确。
因为f(b)=f(d),所以|$2^{b}-1$|=5 - d,所以$2^{b}-1=5 - d,$所以$2^{b}=6 - d,$所以$2^{a}+2^{b}+2^{d}=d - 4+6 - d+2^{d}=2+2^{d}。$
易知$y=2+2^{d}$在(4,5)上单调递增,所以$2+2^{d}∈(18,34),$即$2^{a}+2^{b}+2^{d}∈(18,34),$故D中说法正确。
6.B 作出函数f(x)的图象,如图所示。

作y=|$2^{x}-1$|的图象时,先作$y=2^{x}-1$的图象,再将图象位于x轴下方的部分沿x轴翻折到x轴的上方,其余不变,即可得到y=|$2^{x}-1$|的图象。
因为a<b<c<d且f(a)=f(b)=f(d)<f(c),所以a<0,0<b<1,4<d<5,b<c,但得不出c≥1,故A中说法正确,B中说法错误。
因为f(a)=f(d),所以|$2^{a}-1$|=5 - d,所以$1 - 2^{a}=5 - d,$所以$2^{a}=d - 4,$所以$2^{a}d=d(d - 4)=d^{2}-4d,$易知$y=d^{2}-4d$在(4,5)上单调递增,所以$d^{2}-4d<5,$故C中说法正确。
因为f(b)=f(d),所以|$2^{b}-1$|=5 - d,所以$2^{b}-1=5 - d,$所以$2^{b}=6 - d,$所以$2^{a}+2^{b}+2^{d}=d - 4+6 - d+2^{d}=2+2^{d}。$
易知$y=2+2^{d}$在(4,5)上单调递增,所以$2+2^{d}∈(18,34),$即$2^{a}+2^{b}+2^{d}∈(18,34),$故D中说法正确。
7. (2025河南开封期末)如图,已知直线$x = a$,$x = b(a < b < 0)$与函数$y = 2^{x}$,$y = 4^{x}$的图象分别交于点$A$,$B$,$D$,$C$,且四边形$ABCD$为平行四边形,则(
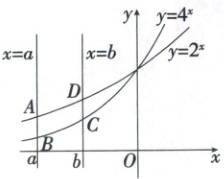
A.$2^{a}+2^{b}=1$
B.$2^{a + 1}+2^{b + 1}=1$
C.$a + b < - 4$
D.$a + b < - 2$
AD
)
A.$2^{a}+2^{b}=1$
B.$2^{a + 1}+2^{b + 1}=1$
C.$a + b < - 4$
D.$a + b < - 2$
答案:
7.AD 由题图得$A(a,2^{a}),$$B(a,4^{a}),$$C(b,4^{b}),$$D(b,2^{b})。$因为四边形ABCD为平行四边形,所以AB=CD,所以$2^{a}-4^{a}=2^{b}-4^{b},$即$2^{a}-2^{b}=4^{a}-4^{b}=(2^{a})^{2}-(2^{b})^{2}=(2^{a}+2^{b})(2^{a}-2^{b})。$
易知$2^{a}-2^{b}≠0,$所以$2^{a}+2^{b}=1,$所以$2^{a + 1}+2^{b + 1}=2,$故A正确,B错误。
由均值不等式得$2^{a}+2^{b}=1≥2\sqrt{2^{a + b}},$所以a + b≤−2,当且仅当a=b=−1时,等号成立。
又a<b<0,所以a + b<−2,故C错误,D正确。
易知$2^{a}-2^{b}≠0,$所以$2^{a}+2^{b}=1,$所以$2^{a + 1}+2^{b + 1}=2,$故A正确,B错误。
由均值不等式得$2^{a}+2^{b}=1≥2\sqrt{2^{a + b}},$所以a + b≤−2,当且仅当a=b=−1时,等号成立。
又a<b<0,所以a + b<−2,故C错误,D正确。
8. (2025四川内江第六中学月考)已知$e = 2.71828·s$,函数$f(x)=a(\frac{1}{e})^{|x|}+b$的图象经过原点,且无限接近于直线$y = e$但不与该直线相交,则(
A.$a = e$
B.$f(x)$的值域为$0,e)$
C.$f(x)$在区间$(0,+\infty)$上单调递减
D.$f(\ln3)=f(\ln\frac{1}{3})$
BD
)A.$a = e$
B.$f(x)$的值域为$0,e)$
C.$f(x)$在区间$(0,+\infty)$上单调递减
D.$f(\ln3)=f(\ln\frac{1}{3})$
答案:
8.BD 因为函数f(x)的图象经过原点,所以a+b=0,即b=−a,所以$f(x)=a(\frac{1}{e})^{|x|}-a。$
又函数f(x)的图象无限接近于直线y=e但不与该直线相交,所以−a=e,所以a=−e,故A错误。
易得$f(x)=−e(\frac{1}{e})^{|x|}+e,$其定义域为R,$f(−x)=−e·(\frac{1}{e})^{|-x|}+e=−e·(\frac{1}{e})^{|x|}+e=f(x),$所以f(x)为偶函数。当x≥0时,$f(x)=−e(\frac{1}{e})^{x}+e∈0,e),$所以函数f(x)的值域为0,e),故B正确。
因为函数$y=(\frac{1}{e})^{x}$为减函数,所以函数$f(x)=−e·(\frac{1}{e})^{|x|}+e$在(0,+∞)上单调递增,故C错误。
因为$\ln\frac{1}{3}=-\ln 3,$f(x)为偶函数,所以$f(\ln\frac{1}{3})=f(\ln 3),$故D正确。
又函数f(x)的图象无限接近于直线y=e但不与该直线相交,所以−a=e,所以a=−e,故A错误。
易得$f(x)=−e(\frac{1}{e})^{|x|}+e,$其定义域为R,$f(−x)=−e·(\frac{1}{e})^{|-x|}+e=−e·(\frac{1}{e})^{|x|}+e=f(x),$所以f(x)为偶函数。当x≥0时,$f(x)=−e(\frac{1}{e})^{x}+e∈0,e),$所以函数f(x)的值域为0,e),故B正确。
因为函数$y=(\frac{1}{e})^{x}$为减函数,所以函数$f(x)=−e·(\frac{1}{e})^{|x|}+e$在(0,+∞)上单调递增,故C错误。
因为$\ln\frac{1}{3}=-\ln 3,$f(x)为偶函数,所以$f(\ln\frac{1}{3})=f(\ln 3),$故D正确。
9. (2025河南青桐鸣大联考)已知实数$a$,$b$满足$\log_{2}\sqrt{3a + 1}+\frac{3}{2}a = 1$,$4^{b}+2b = 3$,则$a - b=$
$-\frac{1}{6}$
.
答案:
9.答案$ -\frac{1}{6}$
解析 由$log_{2}\sqrt{3a + 1}+\frac{3}{2}a = 1,$得$log_{2}\sqrt{3a + 1}=1-\frac{3}{2}a,$所以$\sqrt{3a + 1}=2^{1-\frac{3}{2}a},$所以$3a + 1=2^{2 - 3a},$所以$2^{2 - 3a}+(2 - 3a)-3 = 0。$
由$4^{b}+2b = 3,$得$2^{2b}+2b - 3 = 0,$所以2 - 3a和2b是方程$2^{x}+x - 3 = 0$的两个根。
令$f(x)=2^{x}+x - 3,$易知f(x)在R上单调递增,且f
(1)=0,所以f(2 - 3a)=f(2b)=f
(1)=0,所以2 - 3a = 2b = 1,解得$a=\frac{1}{3},$$b=\frac{1}{2},$所以$a - b=-\frac{1}{6}。$
解析 由$log_{2}\sqrt{3a + 1}+\frac{3}{2}a = 1,$得$log_{2}\sqrt{3a + 1}=1-\frac{3}{2}a,$所以$\sqrt{3a + 1}=2^{1-\frac{3}{2}a},$所以$3a + 1=2^{2 - 3a},$所以$2^{2 - 3a}+(2 - 3a)-3 = 0。$
由$4^{b}+2b = 3,$得$2^{2b}+2b - 3 = 0,$所以2 - 3a和2b是方程$2^{x}+x - 3 = 0$的两个根。
令$f(x)=2^{x}+x - 3,$易知f(x)在R上单调递增,且f
(1)=0,所以f(2 - 3a)=f(2b)=f
(1)=0,所以2 - 3a = 2b = 1,解得$a=\frac{1}{3},$$b=\frac{1}{2},$所以$a - b=-\frac{1}{6}。$
10. (2025广东佛山期末)已知定义在$\mathbf{R}$上的函数$f(x)$满足$f(x + 1)=2f(x)$,当$x\in0,1)$时,$f(x)=3^{x}$,则$f(\frac{5}{2})=$
$4\sqrt{3}$
,不等式$\frac{\sqrt{3}}{2}\leq f(x)\leq2\sqrt{3}$的解集为$[-\frac{1}{2},\frac{3}{2}]$
.
答案:
10.答案$ 4\sqrt{3};$$[-\frac{1}{2},\frac{3}{2}]$
解析 因为f(x + 1)=2f(x),所以$f(\frac{5}{2})=2f(\frac{3}{2})=4f(\frac{1}{2})。$
又当x∈[0,1)时,$f(x)=3^{x},$所以$f(\frac{5}{2})=4f(\frac{1}{2})=4×3^{\frac{1}{2}} = 4\sqrt{3}。$
当x∈[0,1)时,$f(x)=3^{x}∈[1,3),$满足$\frac{\sqrt{3}}{2}\leq f(x)\leq2\sqrt{3}。$
当x∈[1,2)时,x - 1∈[0,1),此时$f(x)=2f(x - 1)=2·3^{x - 1}∈[2,6)。$
由$f(x)=2·3^{x - 1}∈[\frac{\sqrt{3}}{2},2\sqrt{3}],$得$\frac{\sqrt{3}}{4}\leq3^{x - 1}\leq\sqrt{3},$又x∈[1,2),所以$0\leq x - 1\leq\frac{1}{2},$所以$1\leq x\leq\frac{3}{2}。$
当x∈[n,n + 1),n≥2且$n∈N^{*}$时,x - n∈[0,1),此时$f(x)=2f(x - 1)=2^{2}f(x - 2)=·s=2^{n}f(x - n)=2^{n}·3^{x - n}∈[2^{n},3·2^{n}),$不满足$\frac{\sqrt{3}}{2}\leq f(x)\leq2\sqrt{3}。$
当x∈[-1,0)时,x + 1∈[0,1),则$f(x)=\frac{1}{2}f(x + 1)=\frac{1}{2}·3^{x + 1}∈[\frac{1}{2},\frac{3}{2})。$
由$f(x)=\frac{1}{2}·3^{x + 1}∈[\frac{\sqrt{3}}{2},2\sqrt{3}],$得$\sqrt{3}\leq3^{x + 1}\leq4\sqrt{3},$又x∈[-1,0),所以$\frac{1}{2}\leq x + 1<1,$所以$-\frac{1}{2}\leq x<0。$
当x∈[-m,1 - m),m≥2且$m∈N^{*}$时,x + m∈[0,1),此时$f(x)=\frac{1}{2^{m}}f(x + m)∈[\frac{1}{2^{m}},\frac{3}{2^{m}}),$不满足$\frac{\sqrt{3}}{2}\leq f(x)\leq2\sqrt{3}。$
综上,不等式$\frac{\sqrt{3}}{2}\leq f(x)\leq2\sqrt{3}$的解集为$[-\frac{1}{2},\frac{3}{2}]。$
解析 因为f(x + 1)=2f(x),所以$f(\frac{5}{2})=2f(\frac{3}{2})=4f(\frac{1}{2})。$
又当x∈[0,1)时,$f(x)=3^{x},$所以$f(\frac{5}{2})=4f(\frac{1}{2})=4×3^{\frac{1}{2}} = 4\sqrt{3}。$
当x∈[0,1)时,$f(x)=3^{x}∈[1,3),$满足$\frac{\sqrt{3}}{2}\leq f(x)\leq2\sqrt{3}。$
当x∈[1,2)时,x - 1∈[0,1),此时$f(x)=2f(x - 1)=2·3^{x - 1}∈[2,6)。$
由$f(x)=2·3^{x - 1}∈[\frac{\sqrt{3}}{2},2\sqrt{3}],$得$\frac{\sqrt{3}}{4}\leq3^{x - 1}\leq\sqrt{3},$又x∈[1,2),所以$0\leq x - 1\leq\frac{1}{2},$所以$1\leq x\leq\frac{3}{2}。$
当x∈[n,n + 1),n≥2且$n∈N^{*}$时,x - n∈[0,1),此时$f(x)=2f(x - 1)=2^{2}f(x - 2)=·s=2^{n}f(x - n)=2^{n}·3^{x - n}∈[2^{n},3·2^{n}),$不满足$\frac{\sqrt{3}}{2}\leq f(x)\leq2\sqrt{3}。$
当x∈[-1,0)时,x + 1∈[0,1),则$f(x)=\frac{1}{2}f(x + 1)=\frac{1}{2}·3^{x + 1}∈[\frac{1}{2},\frac{3}{2})。$
由$f(x)=\frac{1}{2}·3^{x + 1}∈[\frac{\sqrt{3}}{2},2\sqrt{3}],$得$\sqrt{3}\leq3^{x + 1}\leq4\sqrt{3},$又x∈[-1,0),所以$\frac{1}{2}\leq x + 1<1,$所以$-\frac{1}{2}\leq x<0。$
当x∈[-m,1 - m),m≥2且$m∈N^{*}$时,x + m∈[0,1),此时$f(x)=\frac{1}{2^{m}}f(x + m)∈[\frac{1}{2^{m}},\frac{3}{2^{m}}),$不满足$\frac{\sqrt{3}}{2}\leq f(x)\leq2\sqrt{3}。$
综上,不等式$\frac{\sqrt{3}}{2}\leq f(x)\leq2\sqrt{3}$的解集为$[-\frac{1}{2},\frac{3}{2}]。$
查看更多完整答案,请扫码查看


