《2025年周末C计划高中数学必修第一册人教版》

1. 已知集合 $ A = \{ x | x ^ { 3 } - 8 ＜ 0 \} $，则（A）
A.$ 1 \in A $
B.$ 2 \in A $
C.$ 0 \notin A $
D.$ \{ 0, 1, 2 \} \subseteq A $

答案： 1.A $A = \{x|x^3 - 8 ＜ 0\} = \{x|x ＜ 2\}$，故 $0 \in A$，$1 \in A$，$2 \notin A$，集合$\{0,1,2\}$不是集合$A$的子集，故A正确，B，C，D错误.

2. 若规定 $ \begin{vmatrix} a & b \\ c & d \end{vmatrix} = ad - bc $，则不等式 $ 0 ＜ \begin{vmatrix} 1 & x \\ x & 3 \end{vmatrix} ＜ 2 $ 的解集是（$\{x| - \sqrt{3} ＜ x ＜ - 1或1 ＜ x ＜ \sqrt{3}\}$）
A.$ \{ x | - 1 ＜ x ＜ 1 \} $
B.$ \{ x | - \sqrt { 3 } ＜ x ＜ \sqrt { 3 } \} $
C.$ \{ x | 1 ＜ x ＜ \sqrt { 3 } \} $
D.$ \{ x | - \sqrt { 3 } ＜ x ＜ - 1 $ 或 $ 1 ＜ x ＜ \sqrt { 3 } \} $

答案： 2.D 结合题意，由$0 ＜ \left| \begin{array}{cc}1 & x \\ x & 3\end{array} \right| ＜ 2$得$0 ＜ 3 - x^2 ＜ 2$，所以$1 ＜ x^2 ＜ 3$，所以$-\sqrt{3} ＜ x ＜ -1$或$1 ＜ x ＜ \sqrt{3}$，所以不等式的解集为$\{x| - \sqrt{3} ＜ x ＜ - 1或1 ＜ x ＜ \sqrt{3}\}$.

3. 某生命科学研究所通过研究发现，当一个人的肥胖指数大于 24 但不大于 28 时，可认定为轻微肥胖；当一个人的肥胖指数大于 28 时，可认定为严重肥胖，且轻微肥胖和严重肥胖均为肥胖类型的一种，根据上述文字叙述，可以得知（A）
A.严重肥胖是肥胖指数大于 24 的充分不必要条件
B.严重肥胖是肥胖指数大于 24 的必要不充分条件
C.严重肥胖是肥胖指数大于 24 的充要条件
D.严重肥胖既不是肥胖指数大于 24 的充分条件也不是必要条件

答案： 3.A 解法一：严重肥胖即肥胖指数大于$28$，则一定能推出肥胖指数大于$24$，故充分性成立；当肥胖指数为$25$时，满足大于$24$，但不大于$28$，即不能得出是严重肥胖，故必要性不成立，因此严重肥胖是肥胖指数大于$24$的充分不必要条件.
解法二：由题意知严重肥胖的肥胖指数的取值范围为$(28, + \infty)$.因为$(28, + \infty) \subsetneq (24, + \infty)$，所以严重肥胖是肥胖指数大于$24$的充分不必要条件.

4. 已知函数 $ f ( x ) = | x + 1 | - 1 $，$ g ( x ) = x ^ { 2 } - 2 x - 4 $，若存在 $ a \in \mathbf { R } $，使得 $ f ( a ) - g ( b ) = 0 $，则实数 $ b $ 的取值范围是（D）
A.$ [ - 1, 5 ] $
B.$ [ - 1, 3 ] $
C.$ - 1, + \infty ) $
D.$ ( - \infty, - 1 ] \cup [ 3, + \infty ) $

答案： 4.D
思路点拨：存在$a \in \mathbf{R}$，使得$f(a) - g(b) = 0$，即$f(x)$与$g(x)$的值域有交集，可转化为求函数的值域问题.
解析：因为$f(x) = |x + 1| - 1 \geqslant - 1$，所以函数$f(x)$的值域为$[-1, + \infty)$.若存在$a \in \mathbf{R}$，使得$f(a) - g(b) = 0$成立，即$f(a) = g(b)$，则只需$g(b) \geqslant - 1$，即$b^2 - 2b - 4 \geqslant - 1$，即$b^2 - 2b - 3 = (b - 3)(b + 1) \geqslant 0$，解得$b \in ( - \infty, - 1] \cup [3, + \infty)$.

5. 对于给定实数 $ a $，关于 $ x $ 的一元二次不等式 $ ( a x - 1 ) ( x + 1 ) ＜ 0 $ 的解集可能是（A）
A.$ \left\{ x | - 1 ＜ x ＜ \frac { 1 } { a } \right\} $
B.$ \{ x | x \neq 1 \} $
C.$ \left\{ x | \frac { 1 } { a } ＜ x ＜ - 1 \right\} $
D.$ \mathbf { R } $

答案： 5.A
思路点拨：一元二次不等式的二次项系数为未知参数，其范围会影响不等式的解集，故应对$a$的范围进行分类讨论.
解析：由题意知，$a \neq 0$.当$a ＜ - 1$时，$- \frac{1}{a} ＜ 0$，此时解集为$\left\{ x \mid x ＜ - \frac{1}{a} 或 x ＞ \frac{1}{a} \right\}$；当$a = - 1$时，$- \frac{1}{a} = - 1$，此时解集为$\{x|x \neq - 1\}$；当$- 1 ＜ a ＜ 0$时，$- \frac{1}{a} ＜ - 1$，此时解集为$\left\{ x \mid x ＜ \frac{1}{a} 或 x ＞ - \frac{1}{a} \right\}$；当$a ＞ 0$时，$- 1 ＜ \frac{1}{a}$，此时解集为$\left\{ x \mid - 1 ＜ x ＜ \frac{1}{a} \right\}$，故A正确，B，C，D错误.

6. 有一块半径为 2 的半圆形钢板，计划裁剪成等腰梯形 $ A B C D $ 的形状，它的下底 $ A B $ 是半圆的直径，上底 $ C D $ 的端点在圆周上，则该等腰梯形 $ A B C D $ 的周长 $ y $ 的最大值为（ ）

A.4
B.$ 4 + 4 \sqrt { 2 } $
C.8
D.10

答案：
6.D 如图，作$DE \perp AB$于$E$，连接$BD$，因为$AB$为直径，所以$\angle ADB = 90^{\circ}$，在$Rt \bigtriangleup ADB$与$Rt \bigtriangleup AED$中，$\angle ADB = 90^{\circ} = \angle AED$，$\angle BAD = \angle DAE$，

所以$Rt \bigtriangleup ADB \sim Rt \bigtriangleup AED$，所以$\frac{AD}{AB} = \frac{AE}{AD}$，即$AE = \frac{AD^2}{AB}$.设$AD = x$，因为$AB = 4$，所以$AE = \frac{x^2}{4}$，所以$CD = AB - 2AE = 4 - 2 × \frac{x^2}{4} = 4 - \frac{x^2}{2}$，所以$y = AB + BC + CD + AD = 4 + x + 4 - \frac{x^2}{2} + x = - \frac{1}{2}x^2 + 2x + 8$.由于$AD ＞ 0$，$AE ＞ 0$，$CD ＞ 0$，所以$x ＞ 0$，$4 - \frac{x^2}{2} ＞ 0$，解得$0 ＜ x ＜ 2\sqrt{2}$.故$y$关于$x$的函数解析式为$y = - \frac{1}{2}x^2 + 2x + 8 = - \frac{1}{2}(x - 2)^2 + 10(0 ＜ x ＜ 2\sqrt{2})$.易知当$x = 2$时，$y$取得最大值，为$10$.

7. 定义在 $ \mathbf { R } $ 上的函数 $ y = f ( x ) $ 满足：$ \forall x \in \mathbf { R } $，都有 $ f ( x + 1 ) - f ( x ) \leq x $，$ f ( x + 2 ) - f ( x ) \geq 2 x + 1 $，且 $ f ( 1 ) = 1 $，则 $ f ( 10 ) = $（46）
A.45
B.46
C.91
D.92

答案： 7.B 由$f(x + 1) - f(x) \leqslant x①$，得$f(x + 2) - f(x + 1) \leqslant x + 1②$，$② × (-1)$得$- f(x + 2) + f(x + 1) \geqslant - x - 1③$，又$f(x + 2) - f(x) \geqslant 2x + 1④$，故$③ + ④$得$f(x + 1) - f(x) \geqslant x⑤$，由$①$和$⑤$，得$f(x + 1) - f(x) = x$，所以$f(2) - f(1) = 1$，$f(3) - f(2) = 2$，$f(4) - f(3) = 3$，$·s ·s f(10) - f(9) = 9$，以上式子相加得$f(10) - f(1) = 1 + 2 + 3 + ·s + 9 = 45$，则$f(10) = f(1) + 45 = 46$.

8. 已知 $ x ＞ 0 $，$ x ^ { 2 } - 2 x y + z ^ { 2 } = 0 $，$ x ^ { 2 } ＜ y z $，则（A）
由$x^2 - 2xy + z^2 = 0$，得$2xy = x^2 + z^2$，又$x ＞ 0$，所以$y = \frac{x^2 + z^2}{2x}$，则$y - x = \frac{x^2 + z^2}{2x} - x = \frac{z^2 - x^2}{2x}$.由$x^2 ＜ yz$，得$x^2 ＜ \frac{x^2 + z^2}{2x} · z$，故$2x^3 - x^2z - z^3 ＜ 0$，即$(x - z)(2x^2 + xz + z^2) ＜ 0$，易知$2x^2 + xz + z^2 = 2\left( x + \frac{z}{4} \right)^2 + \frac{7}{8}z^2 ＞ 0$，所以$x - z ＜ 0$，即$0 ＜ x ＜ z$，所以$x^2 ＜ z^2$，所以$y - x = \frac{z^2 - x^2}{2x} ＞ 0$，所以$y ＞ x$.易知$y - z = \frac{x^2 + z^2}{2x} - z = \frac{x^2 + z^2 - 2xz}{2x} = \frac{(x - z)^2}{2x} ＞ 0$，所以$y ＞ z$.综上所述，$y ＞ z ＞ x$.
A.$ y ＞ z ＞ x $
B.$ x ＞ y ＞ z $
C.$ y ＞ x ＞ z $
D.$ z ＞ x ＞ y $

答案： 8.A 由$x^2 - 2xy + z^2 = 0$，得$2xy = x^2 + z^2$，又$x ＞ 0$，所以$y = \frac{x^2 + z^2}{2x}$，则$y - x = \frac{x^2 + z^2}{2x} - x = \frac{z^2 - x^2}{2x}$.由$x^2 ＜ yz$，得$x^2 ＜ \frac{x^2 + z^2}{2x} · z$，故$2x^3 - x^2z - z^3 ＜ 0$，即$(x - z)(2x^2 + xz + z^2) ＜ 0$，易知$2x^2 + xz + z^2 = 2\left( x + \frac{z}{4} \right)^2 + \frac{7}{8}z^2 ＞ 0$，所以$x - z ＜ 0$，即$0 ＜ x ＜ z$，所以$x^2 ＜ z^2$，所以$y - x = \frac{z^2 - x^2}{2x} ＞ 0$，所以$y ＞ x$.易知$y - z = \frac{x^2 + z^2}{2x} - z = \frac{x^2 + z^2 - 2xz}{2x} = \frac{(x - z)^2}{2x} ＞ 0$，所以$y ＞ z$.综上所述，$y ＞ z ＞ x$.

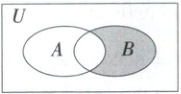
9. 下列集合表示图中阴影部分的为（ABD）

A.$ \complement _ { B } ( A \cap B ) $
B.$ \complement _ { ( A \cup B ) } A $
C.$ A \cup ( \complement _ { U } B ) $
D.$ B \cap ( \complement _ { U } A ) $

答案： 9.ABD 易知图中的阴影部分可表示集合$B$中去除集合$A$与$B$的交集，即$\complement_{B}(A \cap B)$，故A正确；也可表示集合$A$相对于集合$A \cup B$的补集，即$\complement_{(A \cup B)}A$，故B正确；还可表示集合$A$的补集与集合$B$的交集，即$B \cap (\complement_{U}A)$，故D正确.

10. 已知 $ a ＞ 0 $，$ b ＞ 0 $，且 $ \frac { 1 } { a b } = 2 - \frac { 1 } { a } - \frac { 1 } { b } $，则（ACD）
A.$ a + b $ 的最小值为 $ 1 + \sqrt { 3 } $
B.$ a b $ 的最小值为 $ \frac { 1 + \sqrt { 3 } } { 2 } $
C.$ b ＞ \frac { 1 } { 2 } $
D.$ a + 2 b $ 的最小值为 $ \frac { 3 } { 2 } + \sqrt { 6 } $

答案： 10.ACD 由$\frac{1}{a} + \frac{1}{b} = 2 - \frac{1}{a} - \frac{1}{b}$得，$2ab = 1 + a + b$.由$ab \leqslant \left( \frac{a + b}{2} \right)^2$得，$2ab = 1 + a + b \leqslant \frac{(a + b)^2}{2}$，整理得$(a + b)^2 - 2(a + b) - 2 \geqslant 0$，解得$a + b \geqslant 1 + \sqrt{3}(a + b \leqslant 1 - \sqrt{3}$舍去$)$，当且仅当$a = b = \frac{1 + \sqrt{3}}{2}$时等号成立，故$a + b$的最小值为$1 + \sqrt{3}$，A正确.由$a + b \geqslant 2\sqrt{ab}$得，$2ab = 1 + a + b \geqslant 1 + 2\sqrt{ab}$，即$2ab - 2\sqrt{ab} - 1 \geqslant 0$，解得$\sqrt{ab} \geqslant \frac{1 + \sqrt{3}}{2}(\sqrt{ab} \leqslant \frac{1 - \sqrt{3}}{2}$舍去$)$，当且仅当$a = b = \frac{1 + \sqrt{3}}{2}$时等号成立，故$ab$的最小值为$\left( \frac{1 + \sqrt{3}}{2} \right)^2 = 1 + \frac{\sqrt{3}}{2}$，B错误.由$2ab = 1 + a + b$得，$a = \frac{1 + b}{2b - 1} ＞ 0$，所以$2b - 1 ＞ 0$，解得$b ＞ \frac{1}{2}$，故C正确.$a + 2b = \frac{1 + b}{2b - 1} + 2b = \frac{b - \frac{3}{2} + \frac{3}{2}}{2b - 1} + 2b = \frac{3}{2} · \frac{2}{2b - 1} + (2b - 1) + \frac{3}{2} \geqslant \frac{3}{2} + \sqrt{6}$，当且仅当$\frac{3}{2} · \frac{2}{2b - 1} = 2b - 1$，即$b = \frac{2 + \sqrt{6}}{4}$时等号成立，故$a + 2b$的最小值为$\frac{3}{2} + \sqrt{6}$，D正确.

11. 波恩哈德·黎曼是德国著名的数学家。他在数学分析、微分几何方面做出过重要贡献，开创了黎曼几何，并对后来的广义相对论提供了数学基础。他提出了著名的黎曼函数，该函数的定义域为 $ [ 0, 1 ] $，其解析式为 $ R ( x ) = \left\{ \begin{array} { l } { \frac { 1 } { q }, x = \frac { p } { q } ( p, q \in \mathbf { N } ^ { * }, p, q \text { 互质 } ), } \\ { 0, x = 0 \text { 或 } 1 \text { 或 } ( 0, 1 ) \text { 内的无理数, } } \end{array} \right. $ 下列关于黎曼函数的说法正确的是（AB）
A.$ R ( x ) = R ( 1 - x ) $
B.$ R ( a ) R ( b ) \leq R ( a b ) $
C.$ R ( a + b ) \geq R ( a ) + R ( b ) $
D.关于 $ x $ 的不等式 $ R ( x ) ＞ \frac { 1 } { 5 } x + \frac { 1 } { 5 } $ 的解集为 $ \left\{ \frac { 1 } { 2 } \right\} $

答案： 11.AB 对于选项A，当$x = 0$时，$1 - x = 1$，当$x = 1$时，$1 - x = 0$，而$R(0) = R(1) = 0$，故此时满足$R(x) = R(1 - x)$.当$x \in (0,1)$时，$1 - x \in (0,1)$，若$x$是无理数，则$1 - x$是无理数，有$R(x) = R(1 - x) = 0$；若$x$是有理数，则$1 - x$是有理数，当$x = \frac{p}{q}(p,q$为正整数，$\frac{p}{q}$为最简真分数$)$时，$1 - x = 1 - \frac{p}{q} = \frac{q - p}{q}$，$q,q - p$为正整数，$\frac{q - p}{q}$为最简真分数，此时$R(x) = R(1 - x) = \frac{1}{q}$，综上，$x \in [0,1]$时，$R(x) = R(1 - x)$，所以A正确.对于选项B，当$a,b = 0$或$1$或$(0,1)$内的无理数时，$R(a) · R(b) = 0$，$R(ab) = 0$，显然有$R(a)R(b) = R(ab)$；当$a = \frac{p_1}{q_1}$，$b = \frac{p_2}{q_2}(p_1,q_1,p_2,q_2$是正整数，$\frac{p_1}{q_1},\frac{p_2}{q_2}$是最简真分数$)$时，$R(ab) = R\left( \frac{p_1p_2}{q_1q_2} \right) \geqslant \frac{1}{q_1q_2}$，$R(a)R(b) = \frac{1}{q_1q_2}$，故$R(a) · R(b) \leqslant R(ab)$；当$a = 0$，$b = \frac{p}{q}$或$a = \frac{p}{q}$，$b = 0$时，$R(a)R(b) = 0$，$R(ab) = 0$，有$R(a) · R(b) = R(ab)$；当$a = 1$，$b = \frac{p}{q}$或$a = \frac{p}{q}$，$b = 1$时，$R(a)R(b) = 0$，$R(ab) = \frac{1}{q}$，有$R(a)R(b) ＜ R(ab)$；当$a$为$(0,1)$内的无理数，$b = \frac{p}{q}$或$a = \frac{p}{q}$，$b$为$(0,1)$内的无理数时，$R(a)R(b) = 0$，$R(ab) = 0$，有$R(a)R(b) = R(ab)$.综上，$R(a)R(b) \leqslant R(ab)$，所以B正确.对于选项C，取$a = \frac{1}{3}$，$b = \frac{2}{3}$，则$R(a + b) = R(1) = 0$，而$R(a) + R(b) = R\left( \frac{1}{3} \right) + R\left( \frac{2}{3} \right) = \frac{2}{3} ＞ 0$，所以C错误.对于选项D，若$x = 0$或$x = 1$或$x$为$(0,1)$内的无理数，则$R(x) = 0$，显然$R(x) ＞ \frac{1}{5}x + \frac{1}{5}$不成立；若$x = \frac{p}{q}$（$p,q$为正整数，$\frac{p}{q}$为最简真分数），则由$R(x) ＞ \frac{1}{5}x + \frac{1}{5}$，得$\frac{1}{q} ＞ \frac{1}{5} · \frac{p}{q} + \frac{1}{5}$，整理得到$\frac{1}{q} ＞ \frac{p}{5q} + \frac{1}{5}$，整理得到$p + q ＜ 5$，又$p,q$为正整数，$p,q$互质，所以$p = 1$，$q = 2$或$p = 1$，$q = 3$，所以$x$的值为$\frac{1}{2}$或$\frac{1}{3}$，所以D错误.