《2025年周末C计划高中数学必修第一册人教版》

12. (13 分)(1)(2025 浙江杭州第四中学月考)求值：$ 0.25^{-\frac{1}{2}}-(-2×10^{0})^{2}×(2^{-\frac{2}{3}})^{3}+\sqrt[3]{2}×(4^{-\frac{1}{3}})^{-1} $；
(2)$ \frac{(-2\sqrt[3]{a}·\sqrt{b})(3\sqrt[6]{a^{4}b^{2}})}{-4a^{\frac{3}{2}}·\sqrt[6]{b^{3}}}(a,b\gt0) $；
(3)(2025 广东广州二中期中)化简：$ \frac{\sqrt{ab·\sqrt[3]{ab}}}{\sqrt[3]{ab\sqrt{ab}}}+\sqrt[4]{(a - b)^{4}}+\sqrt[3]{(a - b)^{3}}(0\lt a\lt b) $。

答案： 12.解析
$(1)原式=(\frac{1}{4})^{\frac{1}{2}}-(-2)^2×2^{-2}+2^{\frac{1}{2}}×2^{\frac{1}{2}}=2 - 1+2=3. (4分)$
(2)原式$=\frac{(-2a^{\frac{1}{2}}b^{\frac{1}{3}})(3a^{\frac{1}{2}}b^{\frac{1}{2}})}{-4a^{\frac{1}{4}}b^{\frac{5}{6}}}=\frac{3}{2}\frac{ab^{\frac{5}{6}}}{\frac{3}{2}a^{\frac{3}{4}}b^{\frac{5}{6}}}$. (8分)
(3)原式$=\frac{[ab(ab)^{\frac{1}{2}}]^{\frac{1}{3}}}{[ab(ab)^{\frac{1}{2}}]^{\frac{1}{4}}}+(b - a)+(a - b)=\frac{(ab)^{\frac{1}{2}×\frac{1}{3}}}{(ab)^{\frac{1}{4}×\frac{1}{4}}}=\frac{(ab)^{\frac{1}{6}}}{(ab)^{\frac{1}{4}}}=(ab)^{\frac{1}{6}-\frac{1}{4}}=a^{\frac{1}{6}}b^{\frac{1}{6}}$. (13分)

13. (13 分)(2025 江苏徐州邳州毓秀高级中学月考)已知 $ 10^{m}+10^{n}=5,10^{m + n}=6 $，求：
(1)$ \frac{10^{2m}+10^{2n}}{10^{-m}+10^{-n}} $；
(2)$ 10^{\frac{3m + 3n}{2}} $。

答案： 13.解析
(1)对$10^m + 10^n = 5$的两边平方，得$10^{2m}+10^{2n}+2×10^{m + n}=25$，又$10^{m + n}=6$，所以$10^{2m}+10^{2n}=13$. (2分)
易得$10^{-m}+10^{-n}=\frac{1}{10^m}+\frac{1}{10^n}=\frac{10^n + 10^m}{10^{m + n}}=\frac{5}{6}$， (4分)
所以$\frac{10^{2m}+10^{2n}}{10^{-m}+10^{-n}}=\frac{13}{\frac{5}{6}}=\frac{78}{5}$. (6分)
(2)$10^{\frac{m - n}{3}}=(10^{3m - 2n})^{\frac{1}{3}}=\frac{[(10^m)^3]^{\frac{1}{3}}}{[(10^n)^2]^{\frac{1}{3}}}$.
由$10^m + 10^n = 5$和$10^{m + n}=6$，得$10^m = 2,10^n = 3$或$10^m = 3,10^n = 2$.
当$10^m = 2,10^n = 3$时，$10^{\frac{m - n}{3}}=\frac{(2^3)^{\frac{1}{3}}}{\sqrt[3]{3^2}}=\sqrt[3]{\frac{8}{9}}=\frac{2\sqrt[3]{3}}{3}$. (8分)
当$10^m = 3,10^n = 2$时，$10^{\frac{m - n}{3}}=\frac{(3^3)^{\frac{1}{3}}}{\sqrt[3]{2^2}}=\sqrt[3]{\frac{27}{4}}=\frac{3\sqrt[3]{2}}{2}$. (10分)
综上，$10^{\frac{m - n}{3}}=\frac{2\sqrt[3]{3}}{3}$或$\frac{3\sqrt[3]{2}}{2}$ (13分)

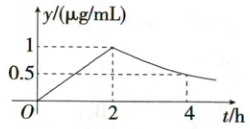
14. (13 分)(2025 河南九校联盟期末)某种药物被服用后，在人体内大致要经过释放和代谢两个主要过程，已知在药物释放过程中，人体血液中的药物浓度 $ y $ (单位：$ \mu g/mL $)与时间 $ t $ (单位：h)成正比，药物释放完毕后，$ y $ 与 $ t $ 的函数关系式为 $ y = ka^{t}(t\geq2,a\gt0 $，且 $ a\neq1,k,a $ 是常数)，如图所示。
(1)根据图象写出 $ y $ 关于 $ t $ 的函数表达式；
(2)据测算，血液中药物的浓度不低于 $ 0.25\mu g/mL $ 时才有效，求该药物的有效时长。

答案： 14.解析
(1)当$0\leqslant t＜2$时，$y$与$t$成正比，且对应图象过点$(0,0)$和$(2,1)$，所以$y=\frac{1}{2}t$. (2分)
当$t\geqslant2$时，$y=ka^t(a＞0$，且$a\neq1)$，且对应图象过点$(2,1)$和$(4,0.5)$，所以$\begin{cases}1=ka^2,\\0.5=ka^4,\end{cases}$所以$\begin{cases}a=\frac{\sqrt{2}}{2},\\k=2,\end{cases}$所以$y=2^{1 - \frac{t}{2}}$. (5分)
所以$y$关于$t$的函数表达式为$y=\begin{cases}\frac{1}{2}t,0\leqslant t＜2,\\2^{1 - \frac{t}{2}},t\geqslant2.\end{cases}$ (6分)
(2)当$0\leqslant t＜2$时，令$\frac{1}{2}t\geqslant0.25$，得$0.5\leqslant t＜2$. (8分)
当$t\geqslant2$时，令$2^{1 - \frac{t}{2}}\geqslant0.25$.
易知$t = 2$时，$2^{1 - \frac{2}{2}}=2^0 = 1＞0.25$；$t = 3$时，$2^{1 - \frac{3}{2}}=\frac{\sqrt{2}}{2}＞0.25$；$t = 4$时，$2^{1 - \frac{4}{2}}=0.5＞0.25$；$t = 5$时，$2^{1 - \frac{5}{2}}=\frac{\sqrt{2}}{4}＞0.25$；$t = 6$时，$2^{1 - \frac{6}{2}}=0.25$；当$t＞6$时，由题知$y$随$t$的增大而减小，所以$2\leqslant t\leqslant6$. (11分)
因此当$0.5\leqslant t\leqslant6$时，药物有效，有效时长为$6 - 0.5 = 5.5(h)$. (13分)