《2025年周末C计划高中数学必修第一册人教版》

9. (2025 广东深圳外国语学校月考)若圆心角为$\frac{2\pi}{3}$的扇形的弦长为$4\sqrt{3}$，则该扇形的弧长为______.

答案：
9.答案$\frac{8\pi}{3}$
解析 设扇形所在圆的圆心为 O.
如图，$\angle AOB=\frac{2\pi}{3}$，$AB = 4\sqrt{3}$，

取弦 AB 的中点 C，连接 OC，则$OC\perp AC$.
易知$\angle AOC=\frac{\pi}{3}$，$AC = 2\sqrt{3}$，
所以在$Rt\triangle ACO$中，$\sin\frac{\pi}{3}=\frac{2\sqrt{3}}{OA}$，
所以$OA = 4$，即扇形的半径为$4$，
所以该扇形的弧长$l=\frac{2\pi}{3}×4=\frac{8\pi}{3}$.

10. (2025 陕西师范大学附属中学月考)已知$\alpha$为锐角，且$2\tan(\pi - \alpha) - 3\cos\left(\frac{\pi}{2}+\beta\right)+5 = 0,\tan(\pi + \alpha)+6\sin(\pi + \beta) - 1 = 0$，则$\sin\alpha =$$\frac{3\sqrt{10}}{10}$.

答案： 10.答案$\frac{3\sqrt{10}}{10}$
解析 由$2\tan(\pi-\alpha)-3\cos(\frac{\pi}{2}+\beta)+5 = 0$，得$-2\tan\alpha+3\sin\beta - 5 = 0$①.
由$\tan(\pi+\alpha)+6\sin(\pi+\beta)-1 = 0$，
得$\tan\alpha-6\sin\beta - 1 = 0$②.
①$×2 -$②，得$3\tan\alpha - 9 = 0$，所以$\tan\alpha = 3$，即$\frac{\sin\alpha}{\cos\alpha}=3$.
又$\sin^{2}\alpha+\cos^{2}\alpha = 1$，所以$\sin^{2}\alpha=\frac{9}{10}$，
又$\alpha$为锐角，所以$\sin\alpha=\frac{3\sqrt{10}}{10}$

11. (13 分)(2025 重庆南岸南坪中学月考)已知$f(\alpha)=\frac{\sin\left(\alpha - \frac{\pi}{2}\right)\cos\left(\frac{3\pi}{2}-\alpha\right)\tan(7\pi - \alpha)}{\tan(-5\pi - \alpha)\sin(\alpha - 3\pi)}$.
(1)化简$f(\alpha)$；
(2)若$\tan\left(\alpha - \frac{3\pi}{2}\right)= - 2$，且$\alpha$为第三象限角，求$f(\alpha)$的值.

答案： 11.解析
(1)$f(\alpha)=\frac{\sin(\alpha-\frac{\pi}{2})\cos(\frac{3\pi}{2}-\alpha)\tan(7\pi-\alpha)}{\tan(-5\pi-\alpha)\sin(\alpha - 3\pi)}$
奇$\pi$当$\pi$看，偶$\pi$当$0$看，
半$\pi$名改变，整$\pi$名不变
$=\frac{-\cos\alpha·(-\sin\alpha)·(-\tan\alpha)}{-\tan\alpha·(-\sin\alpha)}=-\cos\alpha$. (4分)
(2)$\because\tan(\alpha-\frac{3\pi}{2})=\frac{\sin(\alpha-\frac{3\pi}{2})}{\cos(\alpha-\frac{3\pi}{2})}=-\frac{\cos\alpha}{\sin\alpha}=-2$，
$\therefore\frac{\cos\alpha}{\sin\alpha}=2$，即$\sin\alpha=\frac{1}{2}\cos\alpha$， (7分)
又$\sin^{2}\alpha+\cos^{2}\alpha = 1$，$\therefore\frac{1}{4}\cos^{2}\alpha+\cos^{2}\alpha = 1$，即$\cos^{2}\alpha=\frac{4}{5}$， (10分)
$\because\alpha$为第三象限角，$\therefore\cos\alpha=-\frac{2\sqrt{5}}{5}$，
$\therefore f(\alpha)=-\cos\alpha=\frac{2\sqrt{5}}{5}$. (13分)

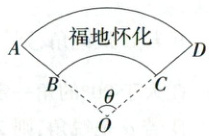
12. (15 分)(2025 湖南怀化期末)为了美化城市，某部门计划在一处绿化带做一个带有“福地怀化”字样的园圃，如图所示，该园圃的形状是扇形$OAD$挖去半径为其一半的扇形$OBC$后得到的扇环$ABCD$，园圃的周长为$50m$，其中圆心角$\theta\in(0,\pi)$，设$AB = xm,0\lt x\leq10$，园圃的面积为$y m^{2}$.
(1)写出$y$关于$x$的函数表达式，并求出该函数的定义域；
(2)当$x$为多少时，$y$最大？求出$y$的最大值及此时$\overset{\frown}{AD}$与$\overset{\frown}{BC}$的长.

答案： 12.解析
(1)由题意得$AB = x\ m$，$OA = 2x\ m$，
故扇形$OAD$的面积为$\frac{1}{2}×\theta×(2x)^{2}=2x^{2}\theta(m^{2})$，
扇形$OBC$的面积为$\frac{1}{2}x^{2}\theta\ m^{2}$，
故$y = 2x^{2}\theta-\frac{1}{2}x^{2}\theta=\frac{3}{2}x^{2}\theta$. (3分)
由弧长公式得$l_{BC}=x\theta\ m$，$l_{AD}=2x\theta\ m$，
故$x\theta+2x\theta+x+x = 50$，解得$\theta=\frac{50 - 2x}{3x}$，
所以$0＜\frac{50 - 2x}{3x}＜\pi$，解得$\frac{50}{3\pi+2}＜x＜25$，
又$x\in(0,10$，故$x\in(\frac{50}{3\pi+2},\ 10$，
故$y=\frac{3}{2}x^{2}×\frac{50 - 2x}{3x}=25x - x^{2}$，其定义域为$(\frac{50}{3\pi+2},\ 10$， (10分)
(2)由二次函数的性质得$y = 25x - x^{2}$在$(\frac{50}{3\pi+2},\ 10$上
单调递增，
所以当$x = 10$时，$y$取得最大值，为$25×10 - 10^{2}=150$， (13分)
此时$\widehat{AD}$的长为$20×\frac{50 - 20}{30}=20(m)$，
$\widehat{BC}$的长为$10×\frac{50 - 20}{30}=10(m)$. (15分)