《2025年周末C计划高中数学必修第一册人教版》

1. (2025 安徽 A10 联盟月考)已知函数$f(x)=\sin x·\cos 2x + 1$，若$f(\alpha)=\frac{1}{2}$，则$f(-\alpha)=$（$\frac{3}{2}$）
A.$0$
B.$\frac{1}{2}$
C.$1$
D.$\frac{3}{2}$

答案： 1.D 易知$f(x)$的定义域为$\mathbf{R}$.
令$g(x)=\sin x\cos 2x$，其定义域为$\mathbf{R}$，$g(-x)=\sin (-x)· \cos (-2x)=-\sin x\cos 2x=-g(x)$，所以$g(x)$为奇函数.
又$f(\alpha )=g(\alpha ) + 1=\frac{1}{2}$，所以$g(\alpha )=-\frac{1}{2}$，所以$g(-\alpha )=-g(\alpha )=\frac{1}{2}$，所以$f(-\alpha )=g(-\alpha ) + 1=\frac{1}{2} + 1=\frac{3}{2}$.

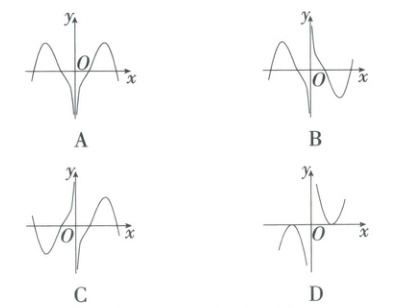
2. (2025 山东泰安期末)函数$f(x)=(x + \frac{2}{x})\cos x$的部分图象大致是（B）

答案： 2.B 易知$f(x)$的定义域为$\{x|x\neq 0\}$，关于原点对称，
$f(-x)=\left(-x + \frac{2}{-x}\right)\cos (-x)=\left(-x - \frac{2}{x}\right)\cos x=-\left(x + \frac{2}{x}\right)\cos x=-f(x)$，所以$f(x)$是奇函数，故排除A.
当$x\in\left(0,\frac{\pi}{2}\right)$时，$x + \frac{2}{x}＞0$，$\cos x＞0$，所以$f(x)＞0$，故排除C.
当$x\in\left(\frac{\pi}{2},\pi\right)$时，$x + \frac{2}{x}＞0$，$\cos x＜0$，所以$f(x)＜0$，故排除D.

3. (2025 江苏苏州期中)在平面直角坐标系$Oxy$中，曲线$g(x)=\cos(2\pi x + \frac{\pi}{6})$与单位圆的交点个数为（ ）

A.$7$
B.$8$
C.$9$
D.$10$

答案：
3.B 易知函数$g(x)$的最小正周期$T = \frac{2\pi}{2\pi}=1$，且$g\left(-\frac{1}{12}\right)=\cos\left(-\frac{\pi}{6} + \frac{\pi}{6}\right)=1$，
在同一平面直角坐标系内作出单位圆和$g(x)=\cos\left(2\pi x + \frac{\pi}{6}\right)$的图象，如图所示.

由图可知，曲线$g(x)=\cos\left(2\pi x + \frac{\pi}{6}\right)$与单位圆的交点个数为8.

4. (2025 浙江嘉兴桐乡期末)已知函数$f(x)=\sin(2\omega x - \frac{\pi}{6}) + b(\omega ＞ 0)$的最小正周期为$T$，且$\frac{2\pi}{3} ＜ T ＜ \frac{3\pi}{2}$，函数$y = f(x + \frac{\pi}{12}) + 1$为奇函数，则$f(\frac{\pi}{4})=$（$\frac{\sqrt{3}}{2}-1$）
A.$\frac{1}{2}$
B.$\frac{\sqrt{3}}{2} - 1$
C.$\frac{\sqrt{3}}{2} + 1$
D.$\frac{3}{2}$

答案： 4.B 易得$f\left(x + \frac{\pi}{12}\right) + 1=\sin\left[2\omega x + \frac{\pi}{6}(\omega - 1)\right] + b + 1$.
因为$y = f\left(x + \frac{\pi}{12}\right) + 1$为奇函数，$\omega＞0$，所以$b + 1 = 0$且$\frac{\pi}{6}(\omega - 1)=k\pi$，$k\in\mathbf{N}$，解得$b = - 1$，$\omega = 6k + 1(k\in\mathbf{N})$①.
因为$\frac{2\pi}{3}＜T＜\frac{3\pi}{2}$，所以$\frac{2\pi}{3}＜\frac{2\pi}{2\omega}＜\frac{3\pi}{2}$，解得$\frac{2}{3}＜\omega＜\frac{3}{2}$②.
结合①②，得$\omega = 1$，所以$f(x)=\sin\left(2x - \frac{\pi}{6}\right)-1$，
所以$f\left(\frac{\pi}{4}\right)=\sin\frac{\pi}{3}-1=\frac{\sqrt{3}}{2}-1$.

5. (2025 湖北武汉部分重点中学联考)已知函数$h(x)=\cos^2x + \frac{1}{2}\sin x - \frac{1}{2}$，若$h(x)$在区间$(0,n\pi)(n\in N^{*})$内恰好有$2025$个零点，则$n$的值为（1350）
A.$2025$
B.$1012$
C.$1350$
D.$1348$

答案： 5.C $h(x)=\cos^{2}x + \frac{1}{2}\sin x - \frac{1}{2}=-\sin^{2}x + \frac{1}{2}\sin x + \frac{1}{2}$
令$\sin x = t$，则$t\in[-1,1]$，$y=-t^{2} + \frac{1}{2}t + \frac{1}{2}$
令$-t^{2} + \frac{1}{2}t + \frac{1}{2}=0$，得$t = -\frac{1}{2}$或$t = 1$，此时$t = \sin x$在$(0,2\pi]$上有三个不相等的实数根.
又$2025 = 675×3$，所以$n\pi = 675×2\pi = 1350\pi$，所以$n = 1350$.

6. (2025 湖北恩施州高中教育联盟期中)已知$\forall x\in R$，$(\sin 2x - a)(e^x + a + 2)\geq 0$，则实数$a$的取值范围是（B）
A.$(-\infty,-2$
B.$[-2,-1]$
C.$[-2,1]$
D.$[1,2]$

答案： 6.B $\because \forall x\in\mathbf{R}$，$(\sin 2x - a)(e^{x} + a + 2)\geqslant 0$，$\therefore \forall x\in\mathbf{R}$，$\sin 2x - a\geqslant 0$，$e^{x} + a + 2\geqslant 0$或$\forall x\in\mathbf{R}$，$\sin 2x - a\leqslant 0$，$e^{x} + a + 2\leqslant 0$.
$\because y = e^{x}$为单调递增函数，$\therefore \forall x\in\mathbf{R}$，$\sin 2x - a\leqslant 0$，$e^{x} + a + 2\leqslant 0$不成立，$\therefore \forall x\in\mathbf{R}$，$\sin 2x - a\geqslant 0$，$e^{x} + a + 2\geqslant 0$，
$\therefore\begin{cases}a\leqslant - 1,\\a + 2\geqslant 0,\end{cases}$
解得$-2\leqslant a\leqslant - 1$.

7. (2025 河南驻马店新蔡第一高级中学月考)已知函数$f(x)=2\sin(\omega x - \frac{\pi}{6})(\omega ＞ 0)$在$(0,\frac{\pi}{3})$上存在最值，且在$(\frac{2\pi}{3},\pi)$上单调，则$\omega$的取值范围是（C）
A.$(0,\frac{2}{3}$
B.$[1,\frac{5}{3}]$
C.$[\frac{5}{2},\frac{8}{3}]$
D.$[\frac{11}{4},\frac{17}{3}]$

答案： 7.C 因为$\omega＞0$，所以当$0＜x＜\frac{\pi}{3}$时，$-\frac{\pi}{6}＜\omega x - \frac{\pi}{6}＜\frac{\pi\omega}{3} - \frac{\pi}{6}$
因为函数$f(x)$在$\left(0,\frac{\pi}{3}\right)$上存在最值，所以$\frac{\pi\omega}{3} - \frac{\pi}{6}\geqslant\frac{\pi}{2}$，
解得$\omega＞2$.
因为$\omega＞0$，所以当$\frac{2\pi}{3}＜x＜\pi$时，$\frac{2\pi\omega}{3} - \frac{\pi}{6}＜\omega x - \frac{\pi}{6}＜\pi\omega - \frac{\pi}{6}$
因为函数$f(x)$在$\left(\frac{2\pi}{3},\pi\right)$上单调，
所以$\left(\frac{2\pi\omega}{3} - \frac{\pi}{6},\pi\omega - \frac{\pi}{6}\right)\subseteq\left(k\pi - \frac{\pi}{2},k\pi + \frac{\pi}{2}\right)$，$k\in\mathbf{Z}$，
所以$\begin{cases}\frac{2\pi\omega}{3} - \frac{\pi}{6}\geqslant k\pi - \frac{\pi}{2},\\\pi\omega - \frac{\pi}{6}\leqslant k\pi + \frac{\pi}{2},\end{cases}$ $k\in\mathbf{Z}$，解得$\frac{3}{2}k - \frac{1}{2}\leqslant\omega\leqslant k + \frac{1}{3}$，$k\in\mathbf{Z}$，所以$\frac{3}{2}k - \frac{1}{2}\leqslant k + \frac{1}{3}$，$k\in\mathbf{Z}$，解得$k\leqslant\frac{7}{3}$，$k\in\mathbf{Z}$.
又因为$\omega＞0$，所以$k\in\{0,1,2\}$.
当$k = 0$时，$0＜\omega\leqslant\frac{2}{3}$；当$k = 1$时，$1\leqslant\omega\leqslant\frac{5}{3}$；当$k = 2$时，$\frac{5}{2}\leqslant\omega\leqslant\frac{8}{3}$.又$\omega＞2$，所以$\omega$的取值范围是$\left[\frac{5}{2},\frac{8}{3}\right]$

8. (2025 福建福州质量检测)已知函数$f(x)=\cos(2x + \varphi)(0 ＜ \varphi ＜ \pi)$的图象关于点$(-\frac{\pi}{3},0)$中心对称，则（BD）
A.$f(x)$在区间$(-\frac{\pi}{3},0)$上单调递增
B.$f(x)$在区间$(-\frac{\pi}{6},\frac{\pi}{6})$上的最大值为$1$
C.直线$x = \frac{2\pi}{3}$是曲线$y = f(x)$的一条对称轴
D.当$x\leq 0$时，函数$y = -\frac{2}{\pi}x + 1$的图象恒在函数$f(x)$图象的上方

答案： 8.BD 因为$f(x)$的图象关于点$\left(-\frac{\pi}{3},0\right)$对称，所以$\varphi - \frac{2\pi}{3} = \frac{\pi}{2} + k\pi$，$k\in\mathbf{Z}$，所以$\varphi = \frac{7\pi}{6} + k\pi$，$k\in\mathbf{Z}$.又$0＜\varphi＜\pi$，所以$\varphi = \frac{\pi}{6}$，所以$f(x)=\cos\left(2x + \frac{\pi}{6}\right)$
对于A，当$x\in\left(-\frac{\pi}{3},0\right)$时，$2x + \frac{\pi}{6}\in\left(-\frac{\pi}{2},\frac{\pi}{6}\right)$，所以函数$f(x)$在区间$\left(-\frac{\pi}{3},0\right)$上不单调，故A错误.
对于B，当$x\in\left(-\frac{\pi}{6},\frac{\pi}{6}\right)$时，$2x + \frac{\pi}{6}\in\left(-\frac{\pi}{6},\frac{\pi}{2}\right)$，所以当$x = \frac{\pi}{12}$时，$f(x)_{\max}=1$，故B正确.
对于C，$f\left(\frac{2\pi}{3}\right)=\cos\frac{9\pi}{6}=\cos\frac{3\pi}{2}=0$，所以直线$x = \frac{2\pi}{3}$不是曲线$y = f(x)$的一条对称轴，故C错误.
对于D，当$x = 0$时，$y = 1$，$f(0)=\cos\frac{\pi}{6}=\frac{\sqrt{3}}{2}＜1$；当$x＜0$时，$y = -\frac{2}{\pi}x + 1＞1$，$f(x)=\cos\left(2x + \frac{\pi}{6}\right)\leqslant 1$，所以函数$y = -\frac{2}{\pi}x + 1$的图象恒在函数$f(x)$图象的上方，故D正确.

9. (2024 广东深圳实验学校期末)已知$x\in R$，用$[x]$表示不超过$x$的最大整数.若函数$f(x)=\sin|x| + |\sin x|$，函数$g(x)=[f(x)]$，则下列说法正确的是（ ）

A.函数$g(x)$是奇函数
B.函数$g(x)$的值域是$\{0,1,2\}$
C.函数$g(x)$的图象关于直线$x = \frac{\pi}{2}$对称
D.方程$\frac{\pi}{2}· g(x)=x$只有一个实数根

答案：
9.BD 易知函数$f(x)$的定义域为$\mathbf{R}$，又$f(-x)=\sin|-x| + |\sin (-x)|=\sin|x| + |\sin x| = f(x)$，所以$g(-x)=[f(-x)] = [f(x)] = g(x)$，又$g(x)$的定义域为$\mathbf{R}$，所以函数$g(x)$是偶函数，故A错误.
当$0\leqslant x\leqslant\pi$时，$f(x)=\sin x + \sin x = 2\sin x$；
当$\pi＜x＜2\pi$时，$f(x)=\sin|x| + |\sin x|=\sin x - \sin x = 0$；
当$2\pi\leqslant x\leqslant 3\pi$时，$f(x)=\sin x + \sin x = 2\sin x$；
$·s·s$
所以函数$f(x)$的部分图象如图所示：

由图可知，当$0\leqslant x＜\frac{\pi}{6}$时，$0\leqslant f(x)＜1$，此时$g(x)=0$；当$\frac{\pi}{6}\leqslant x＜\frac{\pi}{2}$时，$1\leqslant f(x)＜2$，此时$g(x)=1$；当$x = \frac{\pi}{2}$时，$f(x)=2$，此时$g(x)=2$；当$\frac{\pi}{2}＜x\leqslant\frac{5\pi}{6}$时，$1\leqslant f(x)＜2$，此时$g(x)=1$；当$\frac{5\pi}{6}＜x\leqslant\pi$时，$0\leqslant f(x)＜1$，此时$g(x)=0$；当$\pi＜x＜2\pi$时，$f(x)=0$，此时$g(x)=0$；$·s·s$，
易知$2\pi$是$f(x)$的一个周期，所以函数$g(x)$的值域是$\{0,1,2\}$，故B正确.
易得$g\left(-\frac{\pi}{4}\right)=g\left(\frac{\pi}{4}\right)=1$，$g\left(\frac{5\pi}{4}\right)=\left[f\left(\frac{5\pi}{4}\right)\right]=\left[\sin\frac{5\pi}{4}-\sin\frac{5\pi}{4}\right]=0$，所以$g\left(-\frac{\pi}{4}\right)\neq g\left(\frac{5\pi}{4}\right)$，所以函数$g(x)$的图象不关于直线$x = \frac{\pi}{2}$对称，故C错误.
对于方程$\frac{\pi}{2}· g(x)=x$，
当$g(x)=0$时，$x = 0$，$g(0)=0$，此时方程有一个实数根；
当$g(x)=1$时，$x = \frac{\pi}{2}$，$g\left(\frac{\pi}{2}\right)=2\neq 1$，此时方程没有实数根；
当$g(x)=2$时，$x = \pi$，$g(\pi)=[f(\pi)] = 2\sin\pi = 0\neq 2$，此时方程没有实数根.
所以方程$\frac{\pi}{2}· g(x)=x$只有一个实数根，故D正确.