《2025年周末C计划高中数学必修第一册人教版》

1. 学科融合 数学×物理 (2025湖北四校期中联考) 现有一架坏天平，两臂长不等，其余均精确，有人要用它称物体的质量，他将物体放在左右托盘各称一次，记两次称量的结果分别为$a,b(a \neq b)$，设物体的真实质量为$G$,则
(C)
A.$\frac{a+b}{2}=G$　　
B.$\frac{a+b}{2} \leq G$
C.$\frac{a+b}{2}＞G$　　
D.$\sqrt{ab}＜G$

答案： 1.C根据题意，设天平左、右臂的长度分别为$m$，$n$，由两次称量的结果分别为$a$，$b$，得$ma=nG$且$nb=mG$(杠杆原理)，且$a\neq b$，两式联立可得$G^2=ab$，即$G=\sqrt{ab}$，又$\frac{a+b}{2}＞\sqrt{ab}$，所以$\frac{a+b}{2}＞G$.
名师指点
物理中的杠杆原理：动力×动力臂 = 阻力×阻力臂.

2.(2025四川联合性联考)存在狄利克雷函数$f(x)= \begin{cases} 0,x为无理数, \\ 1,x为有理数 , \end{cases}$若$x = (\sqrt{2})^{-1 + y^2},y \in [0,5]$，则$f(x)$的所有值之和为
(D)
A.3　　
B.6　　
C.12　　
D.13

答案： 2.D
思路点拨
分析狄利克雷函数的取值特点，当$x$为无理数时取值均为0，当$x$为有理数时取值均为1，故要求$f(x)$的所有值之和，即求$y\in[0,5]$时$x$的取值为有理数的所有次数，即为$f(x)$的取值为1的所有次数.
解析 令$f(x)=1$，则$x$为有理数，要使$x=(\sqrt{2})^{-1+y^2}$为有理数，则$-1+y^2$必须是偶数，令$-1+y^2=2k(k\in\mathbf{Z})$，则$y^2=2k+1$，因为$y\in[0,5]$，所以$y^2\in[0,25]$，则$0\leq2k + 1\leq25(k\in\mathbf{Z})$，解得$-\frac{1}{2}\leq k\leq12(k\in\mathbf{Z})$，所以$k$的可能取值有0,1,2,3,4,5,6,7,8,9,10,11,12，共13个，所以$f(x)=1$的次数为13，则$f(x)$的所有值之和为13.

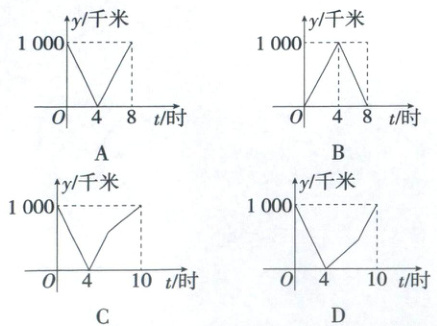
3.(2025江西赣州南康中学开学考试)一列快车从甲地驶往乙地，一列特快车从乙地驶往甲地，快车的速度为100千米/时，特快车的速度为150千米/时，甲、乙两地之间的距离为1000千米，两车同时出发，则图中折线大致表示两车之间的距离$y$(千米)与快车行驶时间$t$(小时)之间的函数图象的是(C)

答案： 3.C当两车同时相向出发时，相遇时间$t_1=1000÷(100 + 150)=4$小时，此时两车之间的距离为0，快车行驶的时间为4小时，故排除B选项；相遇时，快车已经行驶的路程为$100×4=400$千米，还需要行驶$(1000 - 400)÷100=6$小时才能到达乙地，故排除A选项；相遇时，特快车已经行驶的路程为$150×4=600$千米，还需要再行驶$(1000 - 600)÷150=\frac{8}{3}$小时才能到达甲地，所以当特快车停止行驶时，快车还在行驶，此时直线的上升趋势要变缓一些，故排除D选项.

4. 创新题 新考法 (2025江西南昌大学附属学校月考)
为配制一种药液，进行了两次稀释，先在体积为$V$升的桶中盛满纯药液，第一次将桶中药液倒出
5升后用水补满，搅拌均匀，第二次倒出3升后用水补满，若在第二次稀释后桶中药液浓度不超过75%，则$V$的取值可能为
(B)
A.4　　
B.8　　
C.32　　
D.40

答案： 4.B第一次稀释后，药液浓度为$\frac{V - 5}{V}$，第二次稀释后，药液浓度为$\frac{V - 5}{V}×3=\frac{3V - 15}{V}=\frac{V+\frac{15}{V}-8}{V}$，依题意有$\frac{V+\frac{15}{V}-8}{V}\leq75\%$，即$V^2 - 32V + 60\leq0$，解得$2\leq V\leq30$，又$V - 5\geq0$，即$V\geq5$，所以$5\leq V\leq30$.根据选项可知B正确.

5. 强基计划 (2024福建厦门大学强基计划) 对于$a,b,c \in [0,2]$，$\sqrt{|a - b|} + \sqrt{|b - c|} + \sqrt{|c - a|}$的最大值为
($2+\sqrt{2}$)
A.3　　
B.$2 + \sqrt{2}$　　
C.$3\sqrt{2}$　　
D.以上全错

答案： 5.B不妨设$a\geq b\geq c$，则$\sqrt{|a - b|}+\sqrt{|b - c|}+\sqrt{|c - a|}=\sqrt{a - b}+\sqrt{b - c}+\sqrt{a - c}$，因为$\sqrt{a - b}+\sqrt{b - c}\leq\sqrt{2(a - b + b - c)}=\sqrt{2(a - c)}$，当且仅当$\sqrt{a - b}=\sqrt{b - c}$时取等号，所以$\sqrt{|a - b|}+\sqrt{|b - c|}+\sqrt{|c - a|}=\sqrt{a - b}+\sqrt{b - c}+\sqrt{a - c}\leq\sqrt{2(a - c)}+\sqrt{a - c}=(\sqrt{2}+1)\sqrt{a - c}$，由$a\geq b\geq c$，$a,b,c\in[0,2]$可得$0\leq a - c\leq2$，故$(\sqrt{2}+1)\sqrt{a - c}\leq2+\sqrt{2}$，当且仅当$a = 2$，$b = 1$，$c = 0$时等号成立.所以$\sqrt{|a - b|}+\sqrt{|b - c|}+\sqrt{|c - a|}$的最大值为$2+\sqrt{2}$.
名师指点
基本不等式的常见变形
(1)若$a＞0$，$b＞0$，则$\frac{2}{\frac{1}{a}+\frac{1}{b}}\leq\sqrt{ab}\leq\frac{a + b}{2}\leq\sqrt{\frac{a^2 + b^2}{2}}$，此不等式称为重要不等式串.
(2)若$a＞0$，$b＞0$，则$ab\leq(\frac{a + b}{2})^2\leq\frac{a^2 + b^2}{2}$，$a + b\leq\sqrt{2(a^2 + b^2)}$，$\sqrt{a}+\sqrt{b}\leq\sqrt{2(a + b)}$.

6.(2025山东德州、烟台联考)若实数$x,y,z$满足$x + y + z = 0$，且$x ＞ y ＞ z$，则$\frac{y}{\sqrt{x^2 + z^2}}$的取值范围为
(A)
A.$-\frac{\sqrt{5}}{5} ＜ \frac{y}{\sqrt{x^2 + z^2}} ＜ \frac{\sqrt{5}}{5}$　　
B.$-\frac{\sqrt{2}}{2} ＜ \frac{y}{\sqrt{x^2 + z^2}} ＜ \frac{\sqrt{2}}{2}$
C.$-\frac{1}{2} ＜ \frac{y}{\sqrt{x^2 + z^2}} ＜ \frac{1}{2}$　　
D.$-1 ＜ \frac{y}{\sqrt{x^2 + z^2}} ＜ 1$

答案： 6.A因为$x＞y＞z$，$x + y + z = 0$，所以$x＞0$，$z＜0$，所以$(\frac{y}{\sqrt{x^2 + z^2}})^2=\frac{y^2}{x^2 + z^2}=\frac{(x + z)^2}{x^2 + z^2}=1+\frac{2xz}{x^2 + z^2}=1+\frac{2}{\frac{x}{z}+\frac{z}{x}}$，由$x + y + z = 0$得$y=-(x + z)$，又$x＞y＞z$，所以$x＞-(x + z)＞z$，故$-2＜\frac{z}{x}＜\frac{1}{2}$，所以$-\frac{5}{2}＜\frac{z}{x}+\frac{x}{z}\leq - 2$，故$-\frac{1}{2}\leq\frac{1}{\frac{z}{x}+\frac{x}{z}}＜-\frac{2}{5}$，故$0\leq1+\frac{2}{\frac{z}{x}+\frac{x}{z}}＜\frac{1}{5}$，所以$-\frac{\sqrt{5}}{5}＜\frac{y}{\sqrt{x^2 + z^2}}＜\frac{\sqrt{5}}{5}$.

7.(2025上海进才中学期中)已知$a,b,c$是三角形的三边长，对于代数式$\frac{a}{b + c} + \frac{b}{a + c} + \frac{c}{a + b}$，有下列说法：
①有最小值$\frac{3}{2}$，②有最大值3，则
(①)
A.①和②均为真命题
B.①和②均为假命题
C.①为真命题，②为假命题
D.①为假命题，②为真命题

答案： 7.C设$b + c = r$，$a + c = s$，$a + b = t$，则$a=\frac{1}{2}(s + t - r)$，$b=\frac{1}{2}(r + t - s)$，$c=\frac{1}{2}(r + s - t)$，所以$\frac{a}{b + c}+\frac{b}{a + c}+\frac{c}{a + b}=\frac{1}{2}×\frac{s + t - r}{r}+\frac{1}{2}×\frac{r + t - s}{s}+\frac{1}{2}×\frac{r + s - t}{t}=\frac{1}{2}(\frac{s}{r}+\frac{t}{r}+\frac{r}{s}+\frac{t}{s}+\frac{r}{t}+\frac{s}{t})-\frac{3}{2}\geq\frac{1}{2}(2\sqrt{\frac{s}{r}×\frac{r}{s}}+2\sqrt{\frac{t}{r}×\frac{r}{t}}+2\sqrt{\frac{t}{s}×\frac{s}{t}})-\frac{3}{2}=\frac{1}{2}×(2 + 2 + 2)-\frac{3}{2}=\frac{3}{2}$，当且仅当$r = s = t$，即$a = b = c$时等号成立，所以$\frac{a}{b + c}+\frac{b}{a + c}+\frac{c}{a + b}$有最小值$\frac{3}{2}$，故①为真命题.因为$a$，$b$，$c$是三角形的三边长，所以$b + c＞a$，$a + c＞b$，$a + b＞c$，所以$\frac{a + a}{a + b + c}-\frac{a}{b + c}=\frac{2a(b + c)-a(a + b + c)}{(a + b + c)(b + c)}=\frac{a(b + c - a)}{(a + b + c)(b + c)}＞0$，即$\frac{a}{b + c}＜\frac{a + a}{a + b + c}$；$\frac{b + b}{a + b + c}-\frac{b}{a + c}=\frac{2b(a + c)-b(a + b + c)}{(a + b + c)(a + c)}=\frac{b(a + c - b)}{(a + b + c)(a + c)}＞0$，即$\frac{b}{a + c}＜\frac{b + b}{a + b + c}$；$\frac{c + c}{a + b + c}-\frac{c}{a + b}=\frac{2c(a + b)-c(a + b + c)}{(a + b + c)(a + b)}=\frac{c(a + b - c)}{(a + b + c)(a + b)}＞0$，即$\frac{c}{a + b}＜\frac{c + c}{a + b + c}$.所以$\frac{a}{b + c}+\frac{b}{a + c}+\frac{c}{a + b}＜\frac{a + a}{a + b + c}+\frac{b + b}{a + b + c}+\frac{c + c}{a + b + c}=2$，故②为假命题.

8. 经典真题 (2022新高考Ⅱ,12)若$x,y$满足$x^2 + y^2 - xy = 1$，则
(　　BC)
A.$x + y \leq 1$　　
B.$x + y \geq -2$
C.$x^2 + y^2 \leq 2$　　
D.$x^2 + y^2 \geq 1$

答案： 8.BC由$x^2 + y^2 - xy = 1$，得$(x + y)^2 - 1 = 3xy\leq3(\frac{x + y}{2})^2$，当且仅当$x = y=\pm1$时取等号，所以$(x + y)^2\leq4$，即$-2\leq x + y\leq2$，故A错误，B正确；因为$\frac{x^2 + y^2}{2}\leq xy\leq\frac{x^2 + y^2}{2}$，所以$\frac{x^2 + y^2}{2}\leq x^2 + y^2 - 1\leq\frac{x^2 + y^2}{2}$，所以$\frac{2}{3}\leq x^2 + y^2\leq2$，故C正确，D错误.

9.(2025山东济南一中月考)已知关于$x$的一元二次不等式$ax^2 - 2ax + b ＞ 0$的解集为$A = \{x \mid m ＜ x ＜ n\}$，关于$x$的一元二次不等式$ax^2 - 2ax + b ＞ -2$的解集为$B = \{x \mid p ＜ x ＜ q\}$，则
(　　)

A.$A \cap B = B$
B.$A \cup B \subseteq B$
C.$m + n = p + q$
D.当$b ＜ -2$时，$\frac{q}{p} + \frac{2}{q}$的最小值为3

答案：
9.BC因为关于$x$的一元二次不等式$ax^2 - 2ax + b＞0$的解集为$A=\{x|m＜x＜n\}$，所以$a＜0$，且二次函数$y = ax^2 - 2ax + b$的图象与$x$轴有两个交点，其坐标分别为$(m,0)$，$(n,0)$，因为关于$x$的一元二次不等式$ax^2 - 2ax + b＞-2$的解集为$B=\{x|p＜x＜q\}$，所以二次函数$y = ax^2 - 2ax + b$的图象与直线$y = - 2$有两个交点，其坐标分别为$(p,-2)$，$(q,-2)$，画出$y = ax^2 - 2ax + b=a(x - 1)^2 - a + b$的图象，如图所示:由图可得$p＜m＜1＜n＜q$，则$A\subseteq B$，所以$A\cap B = A$，$A\cup B = B$，所以$A\cup B\subseteq B$，故A错误，B正确；易知$m + n = 2$，$p + q = 2$，所以$m + n = p + q$，故C正确；易得$pq=\frac{b + 2}{a}$，又$b＜-2$，所以$b + 2＜0$，所以$pq=\frac{b + 2}{a}＞0$，又$p + q = 2$，所以$p＞0$，$q＞0$，所以$\frac{q}{p}+\frac{p}{q}=\frac{q}{p}+\frac{p + q}{q}=\frac{q}{p}+\frac{p}{q}+1\geq2\sqrt{\frac{q}{p}·\frac{p}{q}}+1 = 3$，当且仅当$\frac{q}{p}=\frac{p}{q}$，即$p = q = 1$时取等号，因为$p＜q$，所以$\frac{q}{p}+\frac{p}{q}＞3$，故D错误.