2025年周末C计划高中数学必修第一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年周末C计划高中数学必修第一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. (2025 河南名校联考)若$6^{x}=25$,$5^{y}=6$,则$xy=$(
A.3
B.$\frac{1}{2}$
C.$\frac{3}{2}$
D.2
2
)A.3
B.$\frac{1}{2}$
C.$\frac{3}{2}$
D.2
答案:
1.D 由 $6^x = 25$, $5^y = 6$,得 $x = \log_6 25$, $y = \log_5 6$,所以 $xy = \log_6 25 × \log_5 6 = 2 \log_6 5 × \log_5 6 = 2$。
2. (2025 湖北鄂东南省级示范高中教育教学改革联盟学校联考)努力公式是一个用来描述努力与结果之间关系的数学公式,它通常表示为$1.01^{365}=37.8$,$0.99^{365}=0.03$。我们可以把$(1 + 1\%)^{365}$看作每天的进步率都是$1\%$,把$(1 - 1\%)^{365}$看作每天的落后率都是$1\%$,则大约经过
A.265
B.266
C.267
D.268
265
天后进步的是落后的 200 倍。$\left(\right.$参考数据:$\lg\frac{1.01}{0.99}\approx0.0087$,$\lg2\approx0.301\left.\right)$( )A.265
B.266
C.267
D.268
答案:
2.A 设 $x$ 天后进步的是落后的 200 倍,则 $\frac{1.01^x}{0.99^x} = 200$,即 $( \frac{1.01}{0.99} )^x = 200$。对其等号左右两边取常用对数,得 $\lg( \frac{1.01}{0.99} )^x = x \lg \frac{1.01}{0.99} = \lg 200 = \lg(2 × 100) = 2 + \lg 2$,所以 $x = \frac{2 + \lg 2}{\lg \frac{1.01}{0.99}} \approx \frac{2.301}{0.0087} \approx 265$,故大约经过 265 天后进步的是落后的 200 倍。
3. (2025 辽宁名校协作体联考)已知$a = 2^{0.3}$,$b = 5^{-0.3}$,$c = 0.2^{0.6}$,则(
A.$b > a > c$
B.$a > c > b$
C.$b > c > a$
D.$a > b > c$
D
)A.$b > a > c$
B.$a > c > b$
C.$b > c > a$
D.$a > b > c$
答案:
3.D 易得 $b = 5^{-0.3} = ( \frac{1}{5} )^{0.3} = 0.2^{0.3}$。
解法一:观察 $a$, $b$,底数不同,指数相同。构造幂函数 $y = x^{0.3}$,易知其在 $(0, +\infty)$ 上单调递增,又 $2 > 0.2$,所以 $2^{0.3} > 0.2^{0.3}$,即 $a > b$。观察 $b$, $c$,底数相同,指数不同。构造指数函数 $y = 0.2^x$,易知其在 $\mathbf{R}$ 上单调递减,又 $0.3 < 0.6$,所以 $0.2^{0.3} > 0.2^{0.6}$,即 $b > c$。综上,$a > b > c$。
解法二:易知 $a = 2^{0.3} > 1$, $b = 0.2^{0.3} \in (0, 1)$, $c = 0.2^{0.6} \in (0, 1)$,所以 $a$ 最大,只需再比较 $b$ 和 $c$ 的大小即可。后续过程同解法一。
解法一:观察 $a$, $b$,底数不同,指数相同。构造幂函数 $y = x^{0.3}$,易知其在 $(0, +\infty)$ 上单调递增,又 $2 > 0.2$,所以 $2^{0.3} > 0.2^{0.3}$,即 $a > b$。观察 $b$, $c$,底数相同,指数不同。构造指数函数 $y = 0.2^x$,易知其在 $\mathbf{R}$ 上单调递减,又 $0.3 < 0.6$,所以 $0.2^{0.3} > 0.2^{0.6}$,即 $b > c$。综上,$a > b > c$。
解法二:易知 $a = 2^{0.3} > 1$, $b = 0.2^{0.3} \in (0, 1)$, $c = 0.2^{0.6} \in (0, 1)$,所以 $a$ 最大,只需再比较 $b$ 和 $c$ 的大小即可。后续过程同解法一。
4. (2025 江苏盐城中学月考)已知$x > 0$,$y > 0$,$\lg4^{x}+\lg2^{y}=\lg8$,则$\frac{1}{2x}+\frac{4}{y}$的最小值是(
A.3
B.$\frac{9}{4}$
C.$\frac{46}{15}$
D.9
3
)A.3
B.$\frac{9}{4}$
C.$\frac{46}{15}$
D.9
答案:
4.A $\because \lg 4^x + \lg 2^y = \lg 8$, $\therefore 4^x · 2^y = 8$, $\therefore 2x + y = 3$,又 $x > 0$, $y > 0$,$\therefore \frac{1}{2x} + \frac{4}{y} = ( \frac{1}{2x} + \frac{4}{y} ) (2x + y) × \frac{1}{3} = \frac{1}{3} (5 + \frac{y}{2x} + \frac{8x}{y} ) \geq \frac{1}{3} (5 + 2 \sqrt{ \frac{y}{2x} · \frac{8x}{y} } ) = 3$,当且仅当 $\frac{y}{2x} = \frac{8x}{y}$,即 $x = \frac{1}{2}$, $y = 2$ 时取等号,故 $\frac{1}{2x} + \frac{4}{y}$ 的最小值为 3。
5. (2025 广东广州二中期中)当$a\neq0$时,函数$y = ax + b$和$y = b^{ax}$在同一坐标系内的图象只可能是(
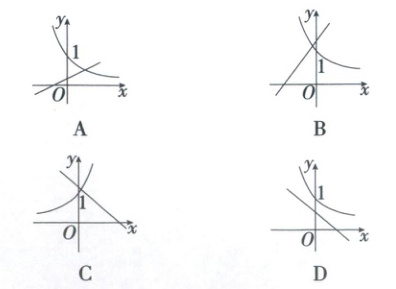
A
)
答案:
5.A
思路点拨:先由函数 $y = ax + b$ 的图象确定 $a$, $b$ 的取值范围,再结合复合函数“同增异减”的原则确定函数 $y = b^{ax}$ 的单调性。
解析:对于 A,由函数 $y = ax + b$ 的图象可知,$a > 0$, $0 < b < 1$,函数 $y = b^{ax}$ 是由 $y = b^u$ 与 $u = ax$ 复合而成的,当 $0 < b < 1$ 时,$y = b^u$ 单调递减,当 $a > 0$ 时,$u = ax$ 单调递增,所以根据复合函数“同增异减”的原则可知,函数 $y = b^{ax}$ 为减函数,故 A 正确。
对于 B,由函数 $y = ax + b$ 的图象可知,$a > 0$, $b > 1$,所以函数 $y = b^{ax}$ 为增函数,故 B 错误。
对于 C,由函数 $y = ax + b$ 的图象可知,$a < 0$, $b > 1$,所以函数 $y = b^{ax}$ 为减函数,故 C 错误。
对于 D,由函数 $y = ax + b$ 的图象可知,$a < 0$, $0 < b < 1$,所以函数 $y = b^{ax}$ 为增函数,故 D 错误。
思路点拨:先由函数 $y = ax + b$ 的图象确定 $a$, $b$ 的取值范围,再结合复合函数“同增异减”的原则确定函数 $y = b^{ax}$ 的单调性。
解析:对于 A,由函数 $y = ax + b$ 的图象可知,$a > 0$, $0 < b < 1$,函数 $y = b^{ax}$ 是由 $y = b^u$ 与 $u = ax$ 复合而成的,当 $0 < b < 1$ 时,$y = b^u$ 单调递减,当 $a > 0$ 时,$u = ax$ 单调递增,所以根据复合函数“同增异减”的原则可知,函数 $y = b^{ax}$ 为减函数,故 A 正确。
对于 B,由函数 $y = ax + b$ 的图象可知,$a > 0$, $b > 1$,所以函数 $y = b^{ax}$ 为增函数,故 B 错误。
对于 C,由函数 $y = ax + b$ 的图象可知,$a < 0$, $b > 1$,所以函数 $y = b^{ax}$ 为减函数,故 C 错误。
对于 D,由函数 $y = ax + b$ 的图象可知,$a < 0$, $0 < b < 1$,所以函数 $y = b^{ax}$ 为增函数,故 D 错误。
6. (2025 山东日照期末)若函数$f(x)=2^{x^{2}-ax + 3}$在区间$(2,3)$上单调递增,则实数$a$的取值范围是(
A.$(-\infty,4$
B.$(-\infty,6$
C.$6,+\infty)$
D.$4,+\infty)$
$(-\infty, 4]$
)A.$(-\infty,4$
B.$(-\infty,6$
C.$6,+\infty)$
D.$4,+\infty)$
答案:
6.A 令 $u = x^2 - ax + 3$,易知其图象开口向上,对称轴方程为 $x = \frac{a}{2}$。易知 $y = 2^x$ 在 $\mathbf{R}$ 上单调递增,又 $f(x) = 2^{x^2 - ax + 3}$ 在 $(2, 3)$ 上单调递增,所以 $u = x^2 - ax + 3$ 在 $(2, 3)$ 上单调递增,所以 $\frac{a}{2} \leq 2$,解得 $a \leq 4$,所以实数 $a$ 的取值范围为 $(-\infty, 4$。
7. (2025 山西晋城部分学校联考)已知函数$f(x)$的定义域为$\mathbf{R}$,$f(x + 3)$为偶函数,若对任意的$x_{1}$,$x_{2}\in[3,+\infty)(x_{1}\neq x_{2})$,都有$\frac{f(x_{1})-f(x_{2})}{x_{1}-x_{2}}>0$,则关于$m$的不等式$f(4^{m}+3)\lt f(2^{m}-3)$的解集为(
A.$(-1,1)$
B.$(1,2)$
C.$(-\infty,1)$
D.$(1,+\infty)$
C
)A.$(-1,1)$
B.$(1,2)$
C.$(-\infty,1)$
D.$(1,+\infty)$
答案:
7.C 因为函数 $f(x + 3)$ 为偶函数,所以 $y = f(x + 3)$ 的图象关于 $y$ 轴对称,所以 $f(x)$ 的图象关于直线 $x = 3$ 对称。$y = f(x + 3)$ 的图象是由 $f(x)$ 的图象向左平移 3 个单位长度得到的。因为对任意的 $x_1$, $x_2 \in 3, +\infty)$ ($x_1 \neq x_2$),都有 $\frac{f(x_1) - f(x_2)}{x_1 - x_2} > 0$,所以函数 $f(x)$ 在 $3, +\infty)$ 上单调递增,所以 $f(x)$ 在 $(-\infty, 3)$ 上单调递减,偶函数在对称区间上的单调性相反。所以由 $f(4^m + 3) < f(2^m - 3)$,得 $|4^m + 3 - 3| < |2^m - 3 - 3|$,故 $4^m < 2^m - 6$ 或 $4^m < 6 - 2^m$,即 $4^m - 2^m + 6 < 0$ 或 $4^m + 2^m - 6 < 0$,所以 $(2^m)^2 - 2^m + 6 < 0$ ① 或 $(2^m)^2 + 2^m - 6 < 0$ ②,显然①无解,由②得 $(2^m + 3) · (2^m - 2) < 0$,所以 $2^m - 2 < 0$,解得 $m < 1$,所以所求解集为 $(-\infty, 1)$。
8. (2025 湖南益阳期末)设函数$f(x)=\begin{cases}-x + 2a,x\leqslant0\\2^{x}-1,x > 0\end{cases}$,则下列说法正确的是(
A.$f(2)=3$
B.若$f(-1)=f(1)$,则$a = 0$
C.若$a > 0$,则$f(x)$的值域为$\mathbf{R}$
D.若$f(x)$的最小值为$-2$,则$a = -1$
ABD
)A.$f(2)=3$
B.若$f(-1)=f(1)$,则$a = 0$
C.若$a > 0$,则$f(x)$的值域为$\mathbf{R}$
D.若$f(x)$的最小值为$-2$,则$a = -1$
答案:
8.ABD 对于 A,$f(2) = 2^2 - 1 = 3$,故 A 正确。
对于 B,由 $f(-1) = f(1)$,得 $1 + 2a = 2 - 1$,解得 $a = 0$,故 B 正确。
对于 C,当 $x \leq 0$ 时,$f(x) = -x + 2a$,其在 $(-\infty, 0$ 上单调递减,所以此时 $f(x) \geq f(0) = 2a$;当 $x > 0$ 时,$f(x) = 2^x - 1$,其在 $(0, +\infty)$ 上单调递增,所以此时 $f(x) > 2^0 - 1 = 0$。因为 $a > 0$,所以 $f(x)$ 的值域为 $(0, +\infty)$,故 C 错误。
对于 D,由 C 中分析得,若 $f(x)$ 存在最小值,则只能满足 $f(x)_{min} = f(0) = 2a = -2$,解得 $a = -1$,故 D 正确。
对于 B,由 $f(-1) = f(1)$,得 $1 + 2a = 2 - 1$,解得 $a = 0$,故 B 正确。
对于 C,当 $x \leq 0$ 时,$f(x) = -x + 2a$,其在 $(-\infty, 0$ 上单调递减,所以此时 $f(x) \geq f(0) = 2a$;当 $x > 0$ 时,$f(x) = 2^x - 1$,其在 $(0, +\infty)$ 上单调递增,所以此时 $f(x) > 2^0 - 1 = 0$。因为 $a > 0$,所以 $f(x)$ 的值域为 $(0, +\infty)$,故 C 错误。
对于 D,由 C 中分析得,若 $f(x)$ 存在最小值,则只能满足 $f(x)_{min} = f(0) = 2a = -2$,解得 $a = -1$,故 D 正确。
9. (2025 安徽逐梦星辰杯大联考)已知$a$,$b$均为正数且$a^{2}-b^{2}=a + b$,则下列不等式正确的有(
A.$\ln(a - b)>0$
B.$a^{2}+b^{2}>1$
C.$2^{a}+2^{b}>4$
D.$2\ln a-\ln b\geqslant\ln4$
BD
)A.$\ln(a - b)>0$
B.$a^{2}+b^{2}>1$
C.$2^{a}+2^{b}>4$
D.$2\ln a-\ln b\geqslant\ln4$
答案:
9.BD 因为 $a$, $b$ 均为正数且 $a^2 - b^2 = (a + b)(a - b) = a + b$,所以 $a - b = 1$。
对于 A,$\ln(a - b) = \ln 1 = 0$,故 A 错误。
对于 B,因为 $a$, $b$ 均为正数且 $a - b = 1$,所以 $a > 1$, $b > 0$,所以 $a^2 > 1$, $b^2 > 0$,所以 $a^2 + b^2 > 1$,故 B 正确。
对于 C,由 B 中分析知 $2^a > 2$, $2^b > 1$,所以 $2^a + 2^b > 3$,故 C 错误。
对于 D,$2 \ln a - \ln b = \ln \frac{a^2}{b} = \ln( b + \frac{1}{b} + 2 ) \geq \ln( 2 \sqrt{b · \frac{1}{b}} + 2 ) = \ln 4$,当且仅当$\begin{cases}b = \frac{1}{b}, \\a = b + 1, \end{cases}$即 $a = 2$, $b = 1$ 时取等号,故 D 正确。
对于 A,$\ln(a - b) = \ln 1 = 0$,故 A 错误。
对于 B,因为 $a$, $b$ 均为正数且 $a - b = 1$,所以 $a > 1$, $b > 0$,所以 $a^2 > 1$, $b^2 > 0$,所以 $a^2 + b^2 > 1$,故 B 正确。
对于 C,由 B 中分析知 $2^a > 2$, $2^b > 1$,所以 $2^a + 2^b > 3$,故 C 错误。
对于 D,$2 \ln a - \ln b = \ln \frac{a^2}{b} = \ln( b + \frac{1}{b} + 2 ) \geq \ln( 2 \sqrt{b · \frac{1}{b}} + 2 ) = \ln 4$,当且仅当$\begin{cases}b = \frac{1}{b}, \\a = b + 1, \end{cases}$即 $a = 2$, $b = 1$ 时取等号,故 D 正确。
10. (2025 湖南三湘名校联盟期中)已知函数$f(x)=3^{\vert ax - 1\vert}(a\neq0)$,则$f(x)$的图象过定点
$(0, 3)$
;$f(x)$的值域为$[1, +\infty)$
。
答案:
10.答案 $(0, 3)$; $[1, +\infty)$
解析:令 $x = 0$,得 $f(0) = 3^{1 - 1} = 3$,所以 $f(x)$ 的图象过定点 $(0, 3)$。易知 $f(x)$ 的定义域为 $\mathbf{R}$,所以函数 $y = |ax - 1|$ 的值域为 $0, +\infty)$,所以 $f(x)$ 的值域为 $1, +\infty)$。
解析:令 $x = 0$,得 $f(0) = 3^{1 - 1} = 3$,所以 $f(x)$ 的图象过定点 $(0, 3)$。易知 $f(x)$ 的定义域为 $\mathbf{R}$,所以函数 $y = |ax - 1|$ 的值域为 $0, +\infty)$,所以 $f(x)$ 的值域为 $1, +\infty)$。
11. (2024 北京丰台期中)若指数函数$f(x)=a^{x}(a > 0$且$a\neq1)$的图象和函数$g(x)=3x + 5(x\geqslant - 1)$的图象相交,则$a$的取值范围是____。
答案:
11.答案 $(0, \frac{1}{2} \cup (1, +\infty)$
解析:当 $a > 1$ 时,指数函数 $f(x) = a^x$ 在 $\mathbf{R}$ 上单调递增,如图 1,$f(x)$ 的图象和 $g(x)$ 的图象一定会相交。

当 $0 < a < 1$ 时,指数函数 $f(x) = a^x$ 在 $\mathbf{R}$ 上单调递减,如图 2,要使 $f(x)$ 的图象与 $g(x)$ 的图象相交,只需 $a^{-1} \geq g(-1) = 2$ 即可,可得 $0 < a \leq \frac{1}{2}$。

综上,$a$ 的取值范围为 $(0, \frac{1}{2} \cup (1, +\infty)$。
易错警示:解决与指数函数单调性、最大(小)值有关的问题时,要注意底数对单调性的影响,当底数含有参数时,要注意对参数进行分类讨论。
11.答案 $(0, \frac{1}{2} \cup (1, +\infty)$
解析:当 $a > 1$ 时,指数函数 $f(x) = a^x$ 在 $\mathbf{R}$ 上单调递增,如图 1,$f(x)$ 的图象和 $g(x)$ 的图象一定会相交。

当 $0 < a < 1$ 时,指数函数 $f(x) = a^x$ 在 $\mathbf{R}$ 上单调递减,如图 2,要使 $f(x)$ 的图象与 $g(x)$ 的图象相交,只需 $a^{-1} \geq g(-1) = 2$ 即可,可得 $0 < a \leq \frac{1}{2}$。

综上,$a$ 的取值范围为 $(0, \frac{1}{2} \cup (1, +\infty)$。
易错警示:解决与指数函数单调性、最大(小)值有关的问题时,要注意底数对单调性的影响,当底数含有参数时,要注意对参数进行分类讨论。
12. (13 分)求下列各式的值:
(1) (2025 云南曲靖凤山中学期末)$2^{\log_{3}+1}-(\sqrt{3}-\sqrt{2})^{0}+\log_{4}9×\log_{3}8$;
(2) (2025 浙江杭州仁和实验学校期末)$\log_{3}18-\log_{3}2+\log_{3}2×\log_{4}3+\log_{3}(\log_{3}27)$;
(3) (2025 江苏连云港灌南惠泽高级中学月考)$\lg5^{2}+\frac{2}{3}\lg8+\lg5×\lg20+(\lg2)^{2}$。
(1) (2025 云南曲靖凤山中学期末)$2^{\log_{3}+1}-(\sqrt{3}-\sqrt{2})^{0}+\log_{4}9×\log_{3}8$;
(2) (2025 浙江杭州仁和实验学校期末)$\log_{3}18-\log_{3}2+\log_{3}2×\log_{4}3+\log_{3}(\log_{3}27)$;
(3) (2025 江苏连云港灌南惠泽高级中学月考)$\lg5^{2}+\frac{2}{3}\lg8+\lg5×\lg20+(\lg2)^{2}$。
答案:
12.解析
(1) 原式 $= 2^{\log_2 3} × 2 - 1 + \frac{2 \lg 3}{2 \lg 2} × \frac{3 \lg 2}{3 \lg 3} = 3 × 2 - 1 + 3 = 8$。(4 分)
(2) 原式 $= \log_3 \frac{18}{2} × \frac{\lg 2}{\lg 3} × \frac{\lg 3}{2 \lg 2} + \log_3 3 = 2 + \frac{1}{2} + 1 = \frac{7}{2}$。(8 分)
(3) 原式 $= 2 \lg 5 + \frac{2}{3} × 3 \lg 2 + \lg 5 × (1 + \lg 2) + (\lg 2)^2 = 2 + 1 - \lg 2 + \lg 2 × \lg 5 + (\lg 2)^2 = 3$。(13 分)
(1) 原式 $= 2^{\log_2 3} × 2 - 1 + \frac{2 \lg 3}{2 \lg 2} × \frac{3 \lg 2}{3 \lg 3} = 3 × 2 - 1 + 3 = 8$。(4 分)
(2) 原式 $= \log_3 \frac{18}{2} × \frac{\lg 2}{\lg 3} × \frac{\lg 3}{2 \lg 2} + \log_3 3 = 2 + \frac{1}{2} + 1 = \frac{7}{2}$。(8 分)
(3) 原式 $= 2 \lg 5 + \frac{2}{3} × 3 \lg 2 + \lg 5 × (1 + \lg 2) + (\lg 2)^2 = 2 + 1 - \lg 2 + \lg 2 × \lg 5 + (\lg 2)^2 = 3$。(13 分)
查看更多完整答案,请扫码查看


