《2025年周末C计划高中数学必修第一册人教版》

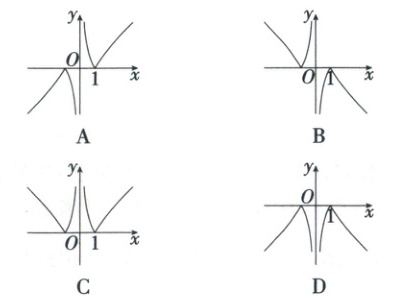
1. （2022 天津，3）函数 $ y = \frac{|x^{2} - 1|}{x} $ 的图象大致为（A）

答案： 1.A 设$f(x)=\frac{\left|x^{2}-1\right|}{x}$，易知其定义域为$\{x|x\neq0\}$，且$f(-x)=\frac{\left|(-x)^{2}-1\right|}{-x}=-\frac{\left|x^{2}-1\right|}{x}=-f(x)$，故函数$f(x)$为奇函数，其图象关于原点对称，故排除C，D；当$x＜0$时，$f(x)=\frac{\left|x^{2}-1\right|}{x}\leq0$，故排除B，故A正确.

2. （2025 湖南名校联盟开学考试）生物学家认为，睡眠中的恒温动物的脉搏率 $ f $（单位：心跳次数 $ · \min^{-1} $）与体重 $ W $（单位：$ kg $）的 $ \frac{1}{3} $ 次方成反比。若 $ A $、$ B $ 为两个睡眠中的恒温动物，$ A $ 的体重为 $ 2 kg $，脉搏率为 $ 210 $ 次 $ · \min^{-1} $，$ B $ 的脉搏率为 $ 70 $ 次 $ · \min^{-1} $，则 $ B $ 的体重为（注：$ (a^{b})^{c} = a^{bc} $）（D）
A.$ 6 kg $
B.$ 8 kg $
C.$ 18 kg $
D.$ 54 kg $

答案： 2.D 根据题意设$f=\frac{k}{W^{÷}}(k\neq0)$.把$W=2$，$f=210$代入，得$k=210×2^{÷}$，所以当$f=70$时，$W^{÷}=\frac{210×2^{÷}}{70}=3×2^{÷}$，所以$W=(3×2^{÷})^{3}=27×2=54$，即B的体重为54kg.

3. （2025 河北石家庄教学质量检测）已知 $ f(x) $ 是定义在 $ \mathbf{R} $ 上的奇函数，当 $ x_{1}, x_{2} \in (0, +\infty) $ 且 $ x_{1} \neq x_{2} $ 时，有 $ \frac{x_{2}f(x_{1}) - x_{1}f(x_{2})}{x_{1}x_{2}(x_{1} - x_{2})} ＞ 0 $ 成立，$ f(2025) = 2025 $，则不等式 $ f(x) - x ＞ 0 $ 的解集为（$(-2025,0)\cup(2025,+\infty)$）
A.$ (-\infty, -2025) \cup (2025, +\infty) $
B.$ (-2025, 0) \cup (2025, +\infty) $
C.$ (-2025, 2025) $
D.$ \left( -\frac{1}{2025}, \frac{1}{2025} \right) $

答案： 3.B
思路点拨
不妨设$x_{1}＜x_{2}$，由$\frac{x_{2}f(x_{1})-x_{1}f(x_{2})}{x_{1}x_{2}(x_{1}-x_{2})}＞0$，得$\frac{x_{2}f(x_{1})-x_{1}f(x_{2})}{x_{1}x_{2}}·\frac{1}{x_{1}-x_{2}}＜0$，从而可构造函数$g(x)=\frac{f(x)}{x}$，其中$x\neq0$，分析函数$g(x)$的单调性与奇偶性，结合已知条件对所求式进行转化即可.
解析 不妨设$x_{1}＜x_{2}$.因为当$x_{1},x_{2}\in(0,+\infty)$且$x_{1}\neq x_{2}$时，有$\frac{x_{2}f(x_{1})-x_{1}f(x_{2})}{x_{1}x_{2}(x_{1}-x_{2})}＞0$成立，所以$\frac{x_{2}f(x_{1})-x_{1}f(x_{2})}{x_{1}x_{2}}=\frac{f(x_{1})}{x_{1}}-\frac{f(x_{2})}{x_{2}}＜0$.构造函数$g(x)=\frac{f(x)}{x}$，其中$x\neq0$，则$g(x_{1})＜g(x_{2})$，
故函数$g(x)$在$(0,+\infty)$上单调递增.
易知$g(-x)=\frac{f(-x)}{-x}=\frac{f(x)}{x}=g(x)$，故函数$g(x)$为偶函数，所以函数$g(x)$在$(-\infty,0)$上单调递减.
因为$f(2025)=2025$，所以$g(-2025)=g(2025)=\frac{f(2025)}{2025}=1$.
当$x＞0$时，由$f(x)-x＞0$得$\frac{f(x)}{x}＞1$，即$g(x)＞g(2025)$，所以$x＞2025$；
当$x＜0$时，由$f(x)-x＞0$得$\frac{f(x)}{x}＜1$，即$g(x)＜g(-2025)$，所以$-2025＜x＜0$.
综上，不等式$f(x)-x＞0$的解集为$(-2025,0)\cup(2025,+\infty)$.

4. （2024 第四届英才杯数学竞赛）已知 $ y = x^{4} - 8x^{2} + 15 - m $ 的图象与 $ x $ 轴有四个不同的交点（不是原点），且每相邻两个交点之间的距离都相等，则 $ m $ 的值为（$\frac{231}{25}$）
A.$ -\frac{\sqrt{231}}{25} $
B.$ \frac{\sqrt{231}}{25} $
C.$ \frac{231}{25} $
D.$ \frac{231}{5} $

答案： 4.C 设四个交点的横坐标自左到右为$x_{1},x_{2},x_{3},x_{4}(x_{1},x_{2},x_{3},x_{4}\neq0)$.易得函数$y=x^{4}-8x^{2}+15-m$为偶函数，偶函数的图象与$x$轴的交点关于$y$轴对称
所以$\begin{cases}x_{2}+x_{3}=0,\\x_{3}-x_{2}=x_{2}-x_{1}\end{cases}$，$\begin{cases}x_{1}=-3x_{3},\\x_{2}=-x_{3},\\x_{4}=3x_{3}\end{cases}$
所以$(x-x_{1})(x-x_{2})(x-x_{3})(x-x_{4})=(x+3x_{3})(x+x_{3})(x-x_{3})(x-3x_{3})=x^{4}-8x^{2}+15-m$，
即$x^{4}-10x_{3}^{2}x^{2}+9x_{3}^{4}=x^{4}-8x^{2}+15-m$，所以$\begin{cases}10x_{3}^{2}=8,\\9x_{3}^{4}=15-m\end{cases}$
所以$m=15-9×(\frac{4}{5})^{2}=\frac{231}{25}$.

5. （2022 新高考Ⅱ，8）已知函数 $ f(x) $ 的定义域为 $ \mathbf{R} $，且 $ f(x + y) + f(x - y) = f(x)f(y) $，$ f(1) = 1 $，则 $ \sum_{k = 1}^{22} f(k) = $（-3）
A.$ -3 $
B.$ -2 $
C.$ 0 $
D.$ 1 $

答案： 5.A 对于$f(x+y)+f(x-y)=f(x)f(y)$，
令$x=1,y=0$，得$2f(1)=f(1)f(0)$，所以$f(0)=2$.
令$x=0$，得$f(y)+f(-y)=2f(y)$，即$f(y)=f(-y)$，所以函数$f(x)$为偶函数.
令$y=1$，得$f(x+1)+f(x-1)=f(x)f(1)=f(x)$，所以$f(x+2)+f(x)=f(x+1)$，所以$f(x+2)=-f(x-1)$，所以$f(x-1)=-f(x-4)$，所以$f(x+2)=f(x-4)$，所以$f(x)=f(x+6)$.
因为$f(2)=f(1)-f(0)=1-2=-1,f(3)=f(2)-f(1)=-1-1=-2,f(4)=f(-2)=f(2)=-1,f(5)=f(-1)=f(1)=1,f(6)=f(0)=2$，所以$f(1)+f(2)+·s+f(6)=0$.
由于22除以6余4，所以$\sum_{k=1}^{22}f(k)=f(1)+f(2)+f(3)+f(4)=1-1-2-1=-3$.
知识拓展
设函数$y=f(x)$，若对任意的$x\in\mathbf{R}$，都有$f(x+T)=f(x)$，则称$T$为函数$f(x)$的一个周期.有如下结论$(a＞0,a\neq b)$：
(1)若$f(x+a)=f(x-a)$，则$T=2a$；
(2)若$f(x+a)=-f(x)$，则$T=2a$；
(3)若$f(x+a)=-\frac{1}{f(x)}$，则$T=2a$；
(4)若$f(x+a)=\frac{1}{f(x)}$，则$T=2a$；
(5)若$f(x+a)=f(x+b)$，则$T=\vert a-b\vert$.

6. （2025 浙江重点高中协作校联考）已知幂函数 $ f(x) $ 的图象过点 $ (4, 2) $，函数 $ g(x) = mf(2x - 1) + 2x - 5 $，$ x \in \left[ \frac{5}{2}, 13 \right] $，若存在实数 $ x $，使得对任意的正实数 $ n $，都有不等式 $ g(x) \leq n + \frac{16}{n} - 21 $ 成立，则实数 $ m $ 的取值范围为（$(-\infty,-6]$）
A.$ (-\infty, -10 $
B.$ (-\infty, -6 $
C.$ 10, +\infty) $
D.$ 6, +\infty) $

答案： 6.B 若对任意的正实数$n$，都有不等式$g(x)\leq n+\frac{16}{n}-21$成立，则$g(x)\leq(n+\frac{16}{n}-21)_{\min}$，$n＞0$.因为$n+\frac{16}{n}-21\geq2\sqrt{n×\frac{16}{n}}-21=-13$，当且仅当$n=\frac{16}{n}$，即$n=4$时，等号成立，所以存在实数$x$，使得不等式$g(x)\leq-13$成立，即$g(x)_{\min}\leq-13$.
由幂函数$f(x)$的图象过点$(4,2)$，得$f(x)=\sqrt{x}(x\geq0)$，故$g(x)=mf(2x-1)+2x-5=m\sqrt{2x-1}+2x-5$.
令$t=\sqrt{2x-1}$，则$2x=t^{2}+1$，所以$g(x)=m\sqrt{2x-1}+2x-5$可化为$h(t)=mt+t^{2}+1-5=t^{2}+mt-4$，此时$g(x)_{\min}=h(t)_{\min}$，即$h(t)_{\min}\leq-13$.
因为$\frac{5}{2}\leq x\leq13$，所以$4\leq2x-1\leq25$，所以$2\leq\sqrt{2x-1}\leq5$，即$2\leq t\leq5$.
易知$h(t)$的图象开口向上，对称轴为直线$t=-\frac{m}{2}$
对称轴方程含参，对其与已知区间的位置关系分类讨论
当$-\frac{m}{2}\leq2$，即$m\geq-4$时，$h(t)$在$[2,5]$上单调递增，故$h(t)_{\min}=h(2)=2m$，所以$2m\leq-13$，解得$m\leq-\frac{13}{2}$，不满足$m\geq-4$，舍去；
当$2＜-\frac{m}{2}＜5$，即$-10＜m＜-4$时，易知$h(t)_{\min}=h(-\frac{m}{2})=\frac{m^{2}}{4}-4$，所以$\frac{m^{2}}{4}-4\leq-13$，解得$m\leq-6$或$m\geq6$，故$-10＜m\leq-6$；
当$-\frac{m}{2}\geq5$，即$m\leq-10$时，$h(t)$在$[2,5]$上单调递减，故$h(t)_{\min}=h(5)=5m+21$，所以$5m+21\leq-13$，解得$m\leq-\frac{34}{5}$，所以$m\leq-10$.
综上，$m\leq-6$.

7. （2024 第二届“鱼塘杯”高考适应性练习）已知 $ f(x) $ 是定义在 $ 0, +\infty) $ 上的单调递增且图象连续不断的函数，且有 $ f(x + y) = \frac{f(x) + f(y)}{1 + f(x)f(y)} $，设 $ x_{1} ＞ x_{2} ＞ 1 $，则下列说法正确的是（D）
令$y=0$，则$f(x)=\frac{f(x)+f(0)}{1+f(x)f(0)}$，所以$f(0)\{[f(x)]^{2}-1\}=0$，因为$f(x)$单调递增，所以$f(x)$不恒等于$\pm1$，故$f(0)=0$，则在$[0,+\infty)$上，有$f(x)\geq f(0)=0$.
下面证明$\forall x\in[0,+\infty),f(x)＜1$.
若存在$x_{0}\in[0,+\infty)$，使得$f(x_{0})=1$，则$f(x+x_{0})=\frac{f(x)+1}{1+f(x)}=1$，此时$f(x)$恒等于1，与$f(x)$单调递增矛盾，故$f(x)\neq1$.
若存在$x_{0}\in[0,+\infty)$，使得$f(x_{0})＞1$，因为$f(x)$的图象是连续不断的，且$f(x_{0})＞1,f(0)=0＜1$，所以一定存在$x\in(0,x_{0})$，使得$f(x)=1$，则与上述$f(x)\neq1$矛盾.故$\forall x\in[0,+\infty),f(x)＜1$.
令$x=x_{1},y=x_{2},x_{1}\neq x_{2}$，则$f(x_{1}+x_{2})=\frac{f(x_{1})+f(x_{2})}{1+f(x_{1})f(x_{2})}＞\frac{[\frac{f(x_{1})+f(x_{2})}{2}]^{2}}{1+[\frac{f(x_{1})+f(x_{2})}{2}]^{2}}$
令$y=x$，则$f(2x)=\frac{2f(x)}{1+[f(x)]^{2}}$，所以$f(x_{1}+x_{2})=\frac{2f(\frac{x_{1}+x_{2}}{2})}{1+[f(\frac{x_{1}+x_{2}}{2})]^{2}}$
当$x\in[0,1)$时，令$g(x)=\frac{2x}{1+x^{2}}$，易知$g(0)=0$，当$x\in(0,1)$时，$g(x)=\frac{2}{\frac{1}{x}+x}$，因为$y=\frac{1}{x}+x$在$(0,1)$上单调递减，所以$g(x)=\frac{2}{\frac{1}{x}+x}$在$[0,1)$上单调递增，所以$g(x)=\frac{2x}{1+x^{2}}$在$[0,1)$上单调递增.
因为$g(f(\frac{x_{1}+x_{2}}{2}))=f(x_{1}+x_{2})$，$g(\frac{f(x_{1})+f(x_{2})}{2})=\frac{\frac{f(x_{1})+f(x_{2})}{2}}{1+[\frac{f(x_{1})+f(x_{2})}{2}]^{2}}$，
所以$g(f(\frac{x_{1}+x_{2}}{2}))＞g(\frac{f(x_{1})+f(x_{2})}{2})$
所以$f(\frac{x_{1}+x_{2}}{2})＞\frac{f(x_{1})+f(x_{2})}{2}$
综上，$1＞f(\frac{x_{1}+x_{2}}{2})＞\frac{f(x_{1})+f(x_{2})}{2}$
A.$ \frac{f(x_{1}) + f(x_{2})}{2} ＞ f\left( \frac{x_{1} + x_{2}}{2} \right) ＞ 1 $
B.$ 1 ＞ \frac{f(x_{1}) + f(x_{2})}{2} ＞ f\left( \frac{x_{1} + x_{2}}{2} \right) $
C.$ f\left( \frac{x_{1} + x_{2}}{2} \right) ＞ \frac{f(x_{1}) + f(x_{2})}{2} ＞ 1 $
D.$ 1 ＞ f\left( \frac{x_{1} + x_{2}}{2} \right) ＞ \frac{f(x_{1}) + f(x_{2})}{2} $

答案： 7.D 令$y=0$，则$f(x)=\frac{f(x)+f(0)}{1+f(x)f(0)}$，所以$f(0)\{[f(x)]^{2}-1\}=0$，因为$f(x)$单调递增，所以$f(x)$不恒等于$\pm1$，故$f(0)=0$，则在$[0,+\infty)$上，有$f(x)\geq f(0)=0$.
下面证明$\forall x\in[0,+\infty),f(x)＜1$.
若存在$x_{0}\in[0,+\infty)$，使得$f(x_{0})=1$，则$f(x+x_{0})=\frac{f(x)+1}{1+f(x)}=1$，此时$f(x)$恒等于1，与$f(x)$单调递增矛盾，故$f(x)\neq1$.
若存在$x_{0}\in[0,+\infty)$，使得$f(x_{0})＞1$，因为$f(x)$的图象是连续不断的，且$f(x_{0})＞1,f(0)=0＜1$，所以一定存在$x\in(0,x_{0})$，使得$f(x)=1$，则与上述$f(x)\neq1$矛盾.故$\forall x\in[0,+\infty),f(x)＜1$.
令$x=x_{1},y=x_{2},x_{1}\neq x_{2}$，则$f(x_{1}+x_{2})=\frac{f(x_{1})+f(x_{2})}{1+f(x_{1})f(x_{2})}＞\frac{[\frac{f(x_{1})+f(x_{2})}{2}]^{2}}{1+[\frac{f(x_{1})+f(x_{2})}{2}]^{2}}$
令$y=x$，则$f(2x)=\frac{2f(x)}{1+[f(x)]^{2}}$，所以$f(x_{1}+x_{2})=\frac{2f(\frac{x_{1}+x_{2}}{2})}{1+[f(\frac{x_{1}+x_{2}}{2})]^{2}}$
当$x\in[0,1)$时，令$g(x)=\frac{2x}{1+x^{2}}$，易知$g(0)=0$，当$x\in(0,1)$时，$g(x)=\frac{2}{\frac{1}{x}+x}$，因为$y=\frac{1}{x}+x$在$(0,1)$上单调递减，所以$g(x)=\frac{2}{\frac{1}{x}+x}$在$[0,1)$上单调递增，所以$g(x)=\frac{2x}{1+x^{2}}$在$[0,1)$上单调递增.
因为$g(f(\frac{x_{1}+x_{2}}{2}))=f(x_{1}+x_{2})$，$g(\frac{f(x_{1})+f(x_{2})}{2})=\frac{\frac{f(x_{1})+f(x_{2})}{2}}{1+[\frac{f(x_{1})+f(x_{2})}{2}]^{2}}$，
所以$g(f(\frac{x_{1}+x_{2}}{2}))＞g(\frac{f(x_{1})+f(x_{2})}{2})$
所以$f(\frac{x_{1}+x_{2}}{2})＞\frac{f(x_{1})+f(x_{2})}{2}$
综上，$1＞f(\frac{x_{1}+x_{2}}{2})＞\frac{f(x_{1})+f(x_{2})}{2}$

8. （2025 重庆第八中学校月考）已知定义域为 $ \mathbf{R} $ 的函数 $ f(x) $ 不是常数函数，当 $ x ＞ 1 $ 时，$ f(x) ＞ 0 $，而且对任意的 $ x, y \in \mathbf{R} $，有 $ f(xy) = f(x)f(y) + f(x) + f(y) $，则下列说法正确的有（ AB）
A.$ f(1) = 0 $
B.若 $ x \in (0, 1) $，则 $ f(x) \in (-1, 0) $
C.$ f(x) $ 在 $ (0, +\infty) $ 上单调递减
D.若 $ f(-1) = 0 $，$ f(3) = 2 $，则不等式 $ f(x - 1) ＜ 8 $ 的解集为 $ \{ x | -3 ＜ x ＜ 5 \} $

答案： 8.AB 对于A，令$x=y=1$，则$f(1)=[f(1)]^{2}+2f(1)$，解得$f(1)=0$或$f(1)=-1$.
当$f(1)=-1$时，由$f(x·1)=f(x)f(1)+f(x)+f(1)$，得$f(x)=f(x)f(1)=-1$，与$f(x)$不是常数函数矛盾，故$f(1)=0$，故A正确.
对于B，令$y=\frac{1}{x}$，则$f(1)=f(x)f(\frac{1}{x})+f(x)+f(\frac{1}{x})$，所以$f(x)=-\frac{1}{1+f(\frac{1}{x})}$
当$x\in(0,1)$时，$\frac{1}{x}＞1$，故$f(\frac{1}{x})＞0$，故$1+f(\frac{1}{x})＞1$，故$f(x)=-1+\frac{1}{1+f(\frac{1}{x})}\in(-1,0)$，故B正确.
对于C，任取$x_{1},x_{2}\in(0,+\infty)$，且$x_{1}＞x_{2}$，令$t=\frac{x_{1}}{x_{2}}$，则$t＞1$，所以$f(t)＞0$，结合B中分析知$f(x_{2})+1＞0$，所以$f(x)=f(tx_{2})=f(t)f(x_{2})+f(t)+f(x_{2})=f(t)[f(x_{2})+1]+f(x_{2})＞f(x_{2})$，故$f(x)$在$(0,+\infty)$上单调递增，故C错误.
对于D，令$y=-1$，则$f(-x)=f(x)f(-1)+f(x)+f(-1)=f(x)$，又函数$f(x)$的定义域为$\mathbf{R}$，故$f(x)$是偶函数，
因为$f(9)=f(3)f(3)+f(3)+f(3)=8$，所以原不等式可转化为$f(\vert x - 1\vert)＜f(9)$，又由C知$f(x)$在$(0,+\infty)$上单调递增，所以$\vert x - 1\vert＜9$，解得$-8＜x＜10$，故D错误.