《2025年周末C计划高中数学必修第一册人教版》

1. (2025 山东师范大学附属中学期中)已知幂函数 $ f(x)=(m^{2}+m - 1)x^{m} $ 的图象与坐标轴没有公共点，则 $ f(m + 4)= $ （$\frac{1}{4}$）
A.$ \frac{1}{2} $
B.$ \sqrt{2} $
C.$ \frac{1}{4} $
D.$ 2\sqrt{2} $

答案： 1.C 因为$f(x)$为幂函数，所以$m^2+m-1=1$，即$m^2+m-2=(m+2)(m-1)=0$，解得$m=-2$或$m=1$，则$f(x)=x^{-2}$或$f(x)=x$，
因为$f(x)$的图象与坐标轴没有公共点，所以$f(x)=x^{-2}$，
幂指数小于0
即$m=-2$，则$f(m+4)=f(2)=2^{-2}=\frac{1}{4}$。

2. (2025 上海交通大学附属中学开学考试)设 $ y = f(x) $ 与 $ y = g(x) $ 是两个不同的幂函数，$ M = \{ x|f(x)=g(x)\} $，则 $ M $ 中元素的个数可能是 （B）
A.$ 0,1,2 $
B.$ 1,2,3 $
C.$ 1,2,3,4 $
D.$ 0,1,2,3 $

答案： 2.B
思路点拨
集合 M中的元素即为方程$f(x)=g(x)$的解，即为幂函数$y=f(x)$和$y=g(x)$的图象的交点的横坐标，从而问题可转化为研究不同幂函数的图象的交点的个数.
解析 设$f(x)=x^a$，$g(x)=x^b$，$a\neq b$.由幂函数的图象可知$f(1)=g(1)=1$，故$f(x)=g(x)$至少存在一个解$x=1$；若$f(x)$，$g(x)$在0处都有定义，则$f(0)=g(0)=0$，故$f(x)=g(x)$可能存在解$x=0$；若$f(x)$，$g(x)$同为奇函数或者同为偶函数，则由图象的对称性可知，$f(-1)=g(-1)=-1$或$f(-1)=g(-1)=1$，故$f(x)=g(x)$可能存在解$x=-1$.综上所述，M中元素的个数可能是1,2,3.

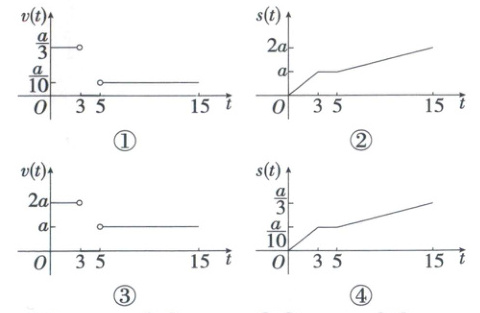
3. (2025 河南平顶山期末)学校宿舍与办公室相距 $ a $ m.某同学有重要材料要交给老师，他从宿舍出发，先匀速跑步 $ 3 $ min 来到办公室，停留 $ 2 $ min，然后匀速步行 $ 10 $ min 返回宿舍.在这个过程中，这位同学行进的速度 $ v(t) $ 和行走的路程 $ s(t) $ 都是关于时间 $ t $ 的函数，则速度函数和路程函数的示意图分别是下面四个图象中的 （A）

A.①②
B.③④
C.①④
D.②③

答案： 3.A 由题意得$v(t)=\begin{cases}\frac{a}{3},&0\leq t＜3,\\0,&3\leq t\leq5,\\ \frac{a}{10},&5＜t\leq15.\end{cases}$
$s(t)=\begin{cases}\frac{at}{3},&0\leq t＜3,\\a,&3\leq t\leq5,\\a+\frac{at}{10},&5＜t\leq15.\end{cases}$
由速度函数及路程函数的解析式可知，其图象分别为①②.

4. (2025 江苏南京六校联合调研)已知幂函数 $ y = x^{m^{2}-2m - 3}(m \in \mathbf{Z}) $ 的图象关于 $ y $ 轴对称，且在 $ (0,+\infty) $ 上单调递减，则满足 $ (a + 1)^{-\frac{1}{3}}＞(3 - 2a)^{-\frac{1}{3}} $ 的实数 $ a $ 的取值范围为 （C）
A.$ (-\infty,-1)\cup(\frac{2}{3},\frac{3}{2}) $
B.$ (-\infty,\frac{2}{3}) $
C.$ (-1,\frac{2}{3})\cup(\frac{3}{2},+\infty) $
D.$ (0,\frac{3}{2}) $

答案： 4.C 因为幂函数$y=x^{m^2-2m-3}$在$(0,+\infty)$上单调递减，所以$m^2-2m-3＜0$，又$m\in\mathbf{Z}$，所以$m=0,1,2$，
又其图象关于$y$轴对称，
所以$m^2-2m-3=(m-3)(m+1)$为偶数，所以$m=1$.
易知函数$y=x^{-\frac{3}{5}}$的定义域为$(-\infty,0)\cup(0,+\infty)$，且函数$y=x^{-\frac{3}{5}}$在$(-\infty,0)$和$(0,+\infty)$上均单调递减，
当$x＜0$时，$y＜0$，当$x＞0$时，$y＞0$，
所以不等式$(a+1)^{-\frac{3}{5}}＞(3-2a)^{-\frac{3}{5}}$可化为$\begin{cases}a+1＞0,\\3-2a＞0,\end{cases}$或$\begin{cases}a+1＜0,\\3-2a＜0,\end{cases}$或$\begin{cases}a+1＞0,\\3-2a＜0,\\a+1＜3-2a\end{cases}$
所以$-1＜a＜\frac{2}{3}$或$a＞\frac{3}{2}$，
所以实数$a$的取值范围为$\left(-1,\frac{2}{3}\right)\cup\left(\frac{3}{2},+\infty\right)$.

5. (2025 湖南天一大联考)已知函数 $ f(x)=x^{3} $，若对任意的正数 $ a,b $，总有 $ f(4a)+f(3b - 4)=0 $，则 $ \frac{1}{2a + 1}+\frac{1}{3b + 2} $ 的最小值为 （B）
A.$ \frac{3 + 2\sqrt{2}}{6} $
B.$ \frac{3 + 2\sqrt{2}}{8} $
C.$ \frac{2 + \sqrt{2}}{2} $
D.$ 1 + \sqrt{2} $

答案： 5.B 易知函数$f(x)=x^3$为定义在$\mathbf{R}$上的奇函数，且为增函数，
因为$f(4a)+f(3b-4)=0$，所以$f(4a)=-f(3b-4)=f(4-3b)$，可得$4a=4-3b$，即$(4a+2)+(3b+2)=8$，
因为$4a+2＞2,3b+2＞2$，
所以$\frac{1}{2a+1}+\frac{1}{3b+2}=\frac{1}{8}[(4a+2)+(3b+2)]\left(\frac{2}{4a+2}+\frac{1}{3b+2}\right)\geq\frac{1}{8}\left[3+2\sqrt{\frac{2(3b+2)}{4a+2}·\frac{4a+2}{3b+2}}\right]=\frac{3+2\sqrt{2}}{8}$，
当且仅当$\frac{2(3b+2)}{4a+2}=\frac{4a+2}{3b+2}$，即$4a+2=\sqrt{2}(3b+2)=8(2-\sqrt{2})$时，等号成立，
所以$\frac{1}{2a+1}+\frac{1}{3b+2}$的最小值为$\frac{3+2\sqrt{2}}{8}$.

6. (2025 辽宁丹东期中)已知函数 $ f(x)=(x - 2)^{\frac{2}{3}}+1 $，对于任意的 $ t \in [-1,2] $，不等式 $ f(2t)+f(a + t)\leq2 $ 恒成立，则实数 $ a $ 的取值范围是 （A）
A.$ (-\infty,-2 $
B.$ (-\infty,-10 $
C.$ -3,+\infty) $
D.$ 7,+\infty) $

答案： 6.A 令$g(x)=x^{\frac{1}{2}}$，则$f(x)=g(x-2)+1$，不等式$f(2t)+f(a+t)\leq2$可化为$g(2t-2)+1+g(a+t-2)+1\leq2$，即$g(2t-2)+g(a+t-2)\leq0$，因为$g(x)=x^{\frac{1}{2}}$是奇函数且在$\mathbf{R}$上单调递增，所以$g(2t-2)\leq-g(a+t-2)=g(-a-t+2)$，则$2t-2\leq-a-t+2$，所以$a\leq-3t+4$在$t\in[-1,2]$上恒成立，则$a\leq-2$，即实数$a$的取值范围是$(-\infty,-2]$.

7. (2025 河南部分学校联考)国庆节期间，甲、乙两商场举行优惠促销活动，甲商场采用“购买所有商品一律打八四折”的促销策略，乙商场采用“购物每满 $ 200 $ 元送 $ 40 $ 元”的促销策略.某顾客计划消费 $ x(x＞0) $ 元，并且要利用商场的优惠活动，使消费更低一些，则 （AC）
A.当 $ 0＜x＜200 $ 时，应进甲商场购物
B.当 $ 200\leq x＜300 $ 时，应进乙商场购物
C.当 $ 400\leq x＜500 $ 时，应进乙商场购物
D.当 $ x＞500 $ 时，应进甲商场购物

答案： 7.AC 当$0＜x＜200$时，甲商场的费用为$0.84x$，乙商场的费用为$x$，$x＞0.84x$，故应进甲商场购物，所以A正确；
当$200\leq x＜300$时，甲商场的费用为$0.84x$，乙商场的费用为$x-40$，$x-40-0.84x=0.16x-40$，当$200\leq x＜250$时，$-8\leq0.16x-40＜0$，即$x-40＜0.84x$，此时应进乙商场购物，当$250＜x＜300$时，$x-40＞0.84x$，此时应进甲商场购物，当$x=250$时两个商场均可，所以B错误；
当$400\leq x＜500$时，甲商场的费用为$0.84x$，乙商场的费用为$x-80$，$x-80-0.84x=0.16x-80$，因为$400\leq x＜500$，所以$-16\leq0.16x-80＜0$，故$x-80＜0.84x$，所以应进乙商场购物，所以C正确；
假设消费了600元，则在甲商场购物的费用为$600×0.84=504$元，在乙商场购物的费用为$600-120=480$元，乙商场购物的费用更低，故应进乙商场购物，故D错误.

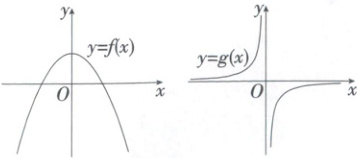
8. (2025 浙江杭州期中)已知函数 $ y = f(x) $ 与 $ y = g(x) $ 的图象如图所示，则 （AC）

A.$ y = f(x)g(x) $ 为奇函数
B.$ y = f(x)g(x) $ 在 $ (0,+\infty) $ 上单调递增
C.$ y = f(g(x)) $ 在 $ (-\infty,0) $ 上单调递减
D.$ y = f(x)g(x) $ 的值域不能为 $ \mathbf{R} $

答案： 8.AC 由题中图象知，$y=f(x)$，$x\in\mathbf{R}$是偶函数，在$(-\infty,0)$上单调递增，在$(0,+\infty)$上单调递减；$y=g(x)$，$x\in(-\infty,0)\cup(0,+\infty)$是奇函数，在$(-\infty,0)$，$(0,+\infty)$上单调递增.
对于A，$y=f(x)g(x)$的定义域为$(-\infty,0)\cup(0,+\infty)$，
因为$f(-x)g(-x)=f(x)[-g(x)]=-f(x)g(x)$，所以$y=f(x)g(x)$是奇函数，故A正确；
对于B，不妨令$f(x)=1-x^2$，$g(x)=-\frac{1}{x^3}$，符合题意，
则$f(x)g(x)=-\frac{1}{x^3}+\frac{1}{x}$，取$x=2$和$x=3$，满足$2＜3$，
但$f(2)g(2)=\frac{1}{2}-\frac{1}{8}=\frac{3}{8}＞f(3)g(3)=\frac{1}{3}-\frac{1}{27}=\frac{8}{27}$，故B
错误；
对于C，$\forall x_1,x_2\in(-\infty,0)$，$x_1＜x_2$，由题中图象知$g(x_1)＞0$，$g(x_2)＞0$，因为$g(x)$在$(-\infty,0)$上单调递增，所以$0＜g(x_1)＜g(x_2)$，又因为$f(x)$在$(0,+\infty)$上单调递减，所以$f(g(x_1))＞f(g(x_2))$，即$y=f(g(x))$在$(-\infty,0)$上单调递减，故C正确；
对于D，由A得$y=f(x)g(x)$为奇函数，故可只研究$x＞0$的部分，设$y=f(x)$的图象与$x$轴正半轴交于点$(x_0,0)$，则当$x$趋近于0时，$y=f(x)g(x)$的值趋近于$-\infty$，在$(0,x_0)$内，$y=f(x)g(x)$的值随$x$的增大而增大，当$x=x_0$时，$y=f(x)g(x)$的值为0，当$x$趋近于$+\infty$时，$y=f(x)g(x)$的值趋近于0，但比0大，故此时$y=f(x)g(x)$能取到$(-\infty,0]$的一切值，同理，当$x＜0$时，$y=f(x)g(x)$能取到$[0,+\infty)$的一切值，故$y=f(x)g(x)$的值域能为$\mathbf{R}$，故D错误.