21. (本小题满分6分)
在一个不透明的口袋中装有3个完全相同的小球,在球面上分别写上数字1,2,3,从口袋中随机摸出一个小球,记录下数字后放回,再随机摸出一个小球.
(1)求第一次摸出的小球上的数字为奇数的概率.
(2)请用画树状图或列表的方法求两次摸出的小球上的数字之和不小于3的概率.
在一个不透明的口袋中装有3个完全相同的小球,在球面上分别写上数字1,2,3,从口袋中随机摸出一个小球,记录下数字后放回,再随机摸出一个小球.
(1)求第一次摸出的小球上的数字为奇数的概率.
(2)请用画树状图或列表的方法求两次摸出的小球上的数字之和不小于3的概率.
答案:
(1)
口袋中一共有$3$个完全相同的小球,数字为$1$,$2$,$3$,其中奇数有$1$,$3$共$2$个。
根据概率公式$P(A)=\frac{m}{n}$(其中$n$是总情况数,$m$是事件$A$发生的情况数),可得第一次摸出的小球上的数字为奇数的概率$P = \frac{2}{3}$。
(2)
画树状图如下:
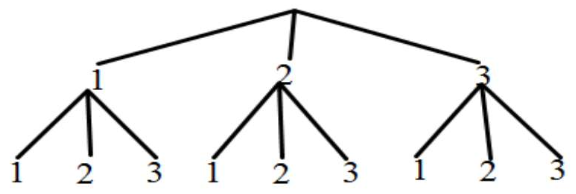
总共有$9$种等可能的结果,两次摸出的小球上的数字之和不小于$3$的结果有$8$种。
所以两次摸出的小球上的数字之和不小于$3$的概率$P=\frac{8}{9}$。
综上,答案为:
(1)$\frac{2}{3}$;
(2)$\frac{8}{9}$。
(1)
口袋中一共有$3$个完全相同的小球,数字为$1$,$2$,$3$,其中奇数有$1$,$3$共$2$个。
根据概率公式$P(A)=\frac{m}{n}$(其中$n$是总情况数,$m$是事件$A$发生的情况数),可得第一次摸出的小球上的数字为奇数的概率$P = \frac{2}{3}$。
(2)
画树状图如下:

总共有$9$种等可能的结果,两次摸出的小球上的数字之和不小于$3$的结果有$8$种。
所以两次摸出的小球上的数字之和不小于$3$的概率$P=\frac{8}{9}$。
综上,答案为:
(1)$\frac{2}{3}$;
(2)$\frac{8}{9}$。
22. (本小题满分7分)
如图是A,B两个可以自由转动的转盘,指针固定不动,转盘各被等分成三个扇形,并分别标上-1,2,3和-4,-6,8这六个数字. 同时转动两个转盘各一次(指针落在等分线时重转),转盘自由停止后,A转盘中指针指向的数字记为$x$,B转盘中指针指向的数字记为$y$,点$Q$的坐标记为$Q(x, y)$.
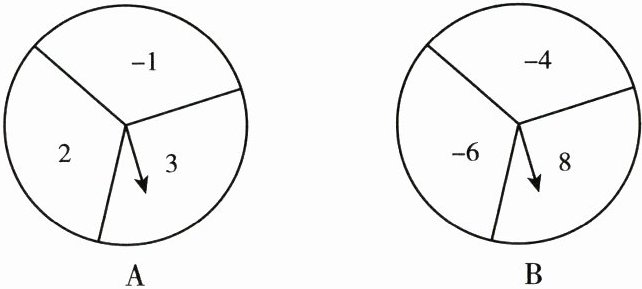
(1)用列表或画树状图的方法表示$(x, y)$所有可能出现的结果.
(2)求出点$Q(x, y)$落在第四象限的概率.
如图是A,B两个可以自由转动的转盘,指针固定不动,转盘各被等分成三个扇形,并分别标上-1,2,3和-4,-6,8这六个数字. 同时转动两个转盘各一次(指针落在等分线时重转),转盘自由停止后,A转盘中指针指向的数字记为$x$,B转盘中指针指向的数字记为$y$,点$Q$的坐标记为$Q(x, y)$.

(1)用列表或画树状图的方法表示$(x, y)$所有可能出现的结果.
(2)求出点$Q(x, y)$落在第四象限的概率.
答案:
解:
(1) 画树状图如下:
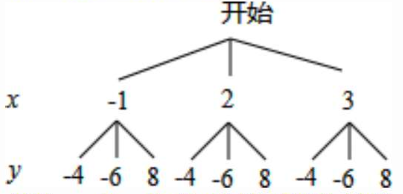
共有9种等可能结果。
(2)第四象限点需满足 $x>0$ 且 $y<0$。符合条件的点有:(2,-4),(2,-6),(3,-4),(3,-6),共4种。
解:
(1) 画树状图如下:

共有9种等可能结果。
(2)第四象限点需满足 $x>0$ 且 $y<0$。符合条件的点有:(2,-4),(2,-6),(3,-4),(3,-6),共4种。
概率 $P=\frac{4}{9}$。
查看更多完整答案,请扫码查看


