《2025年云南省标准教辅优佳学案配套测试卷九年级数学上册人教版》

26. (本小题满分8分)
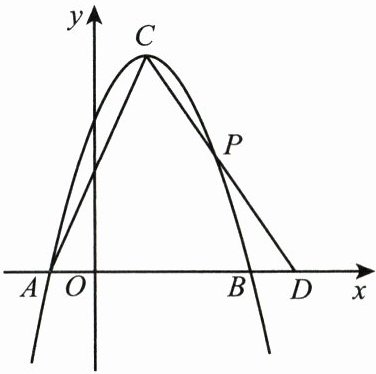
抛物线$y = ax^2 + bx + 3$过点$A(-1, 0)$，点$B(3, 0)$，顶点为$C$.
(1)求抛物线对应的函数解析式及点$C$的坐标.
(2)如图，点$P$在$x$轴上方的抛物线上，连接$CP$并延长交$x$轴于点$D$，连接$AC$. 若$\triangle DAC$是等腰三角形，求点$D$的坐标.

答案：
(1) 因为抛物线$y=ax^2+bx+3$过点$A(-1,0)$，$B(3,0)$，设抛物线解析式为$y=a(x+1)(x-3)$。展开得$y=a(x^2-2x-3)=ax^2-2ax-3a$，由常数项$-3a=3$，解得$a=-1$，故解析式为$y=-(x+1)(x-3)=-x^2+2x+3$。顶点$C$的横坐标为$x=-\frac{b}{2a}=-\frac{2}{2×(-1)}=1$，代入得$y=-(1)^2+2×1+3=4$，所以顶点$C(1,4)$。
(2) 设$D(d,0)$，$A(-1,0)$，$C(1,4)$，$AC=\sqrt{(1+1)^2+(4-0)^2}=2\sqrt{5}$，$DA=|d+1|$，$DC=\sqrt{(d-1)^2+16}$。
情况1：$DA=DC$
$|d+1|=\sqrt{(d-1)^2+16}$，平方得$(d+1)^2=(d-1)^2+16$，解得$d=4$，即$D(4,0)$。
情况2：$DA=AC$
$|d+1|=2\sqrt{5}$，解得$d=-1\pm2\sqrt{5}$，即$D(-1+2\sqrt{5},0)$或$D(-1-2\sqrt{5},0)$。
情况3：$DC=AC$
$\sqrt{(d-1)^2+16}=2\sqrt{5}$，平方得$(d-1)^2=4$，解得$d=3$或$d=-1$，此时$D$与$B$或$A$重合，无符合条件的$P$点，舍去。
综上，点$D$的坐标为$(4,0)$，$(-1+2\sqrt{5},0)$，$(-1-2\sqrt{5},0)$。
(1) 解析式：$y=-x^2+2x+3$，顶点$C(1,4)$；
(2) $D(4,0)$，$(-1+2\sqrt{5},0)$，$(-1-2\sqrt{5},0)$。