《2025年云南省标准教辅优佳学案配套测试卷九年级数学上册人教版》

25. (本小题满分7分)
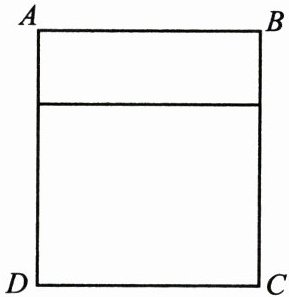
如图，用一根长60 cm的铁丝做成一个“日”字形矩形框架$ABCD$，铁丝恰好全部用完.
(1)若所做成的矩形框架$ABCD$的面积为144 $cm^2$，则$AB$的长为多少厘米？
(2)矩形框架$ABCD$面积的最大值为多少平方厘米？

答案：
(1)设AB的长为$x$cm，AD的长为$y$cm。
“日”字形框架由3条横向边（AB方向）和2条纵向边（AD方向）组成，铁丝总长60cm，故$3x + 2y = 60$，则$y=\frac{60 - 3x}{2}$。
矩形面积为$xy = 144$，代入得：
$x·\frac{60 - 3x}{2}=144$
化简：$60x - 3x^2 = 288$
即$x^2 - 20x + 96 = 0$
解得$x_1=12$，$x_2=8$。
均为正数，故AB的长为12cm或8cm。
(2)面积$S=xy=x·\frac{60 - 3x}{2}=-\frac{3}{2}x^2 + 30x$。
二次函数$S=-\frac{3}{2}x^2 + 30x$开口向下，对称轴$x=-\frac{30}{2×(-\frac{3}{2})}=10$。
当$x=10$时，$S_{max}=-\frac{3}{2}×10^2 + 30×10=150$。
(1)12cm或8cm；
(2)150cm²。