《2025年云南省标准教辅优佳学案配套测试卷九年级数学上册人教版》

15. 如图所示的转盘被划分成六个大小相同的扇形，并在六个扇形内分别标上数字1，2，3，4，5，6，指针停在每个扇形的可能性相等，四位同学各自发表了下述见解：

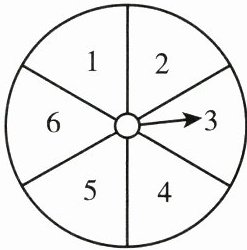
甲：如果指针前三次都停在了3号扇形内，下次就一定不会停在3号扇形内了.
乙：只要指针连续转六次，一定会有一次停在6号扇形内.
丙：指针停在奇数号扇形内的概率和停在偶数号扇形内的概率相等.
丁：运气好的时候，只要在转动前默默想好让指针停在6号扇形内，指针停在6号扇形内的可能性就会加大.
其中正确的见解有().

A.1个
B.2个
C.3个
D.4个

答案： A

16. 从$\sqrt{2}$，0，$\pi$，$\frac{22}{7}$，6这五个数中随机抽取一个数，抽到有理数的概率是.

答案： $\frac{3}{5}$

17. 在一个不透明的口袋中装有2个白球和$n$个黄球，它们除颜色外无其他差别. 若从中随机摸出一个球，摸到黄球的概率是$\frac{4}{5}$，则$n =$.

答案： $8$

18. 在一个不透明的袋子中装有若干个材质、大小完全相同的红球，小明在袋子中放入3个黑球(每个黑球除颜色外其余都与红球相同)，摇匀后，每次随机从袋子中摸出一个球，记录颜色后放回袋子中，通过大量重复摸球试验后发现，摸到红球的频率稳定在0.85左右，估计袋子中红球有个.

答案： $17$。

19. 如图，共有12个大小相同的小正方形，其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分. 现从其余的小正方形中任选一个涂上阴影，能够构成这个正方体的表面展开图的概率是.

答案： 3/7

20. (本小题满分7分)
九年级(8)班从三名男生(含小强)和五名女生中选四名学生参加学校举行的“中华古诗文朗诵大赛”，规定女生选$n$名.
(1)当$n$为何值时，男生小强参加是必然事件？
(2)当$n$为何值时，男生小强参加是不可能事件？
(3)当$n$为何值时，男生小强参加是随机事件？

答案：
(1)$1$；
(2)$4$；
(3)$2$或$3$。