22. (本小题满分8分)
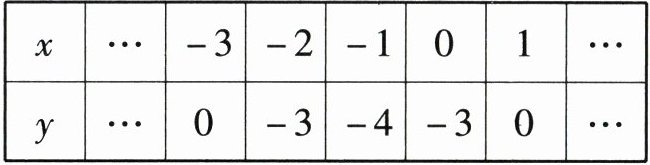
一个二次函数图象上部分点的横坐标$x$与纵坐标$y$的对应值如下表所示.
(1)求这个二次函数的解析式.
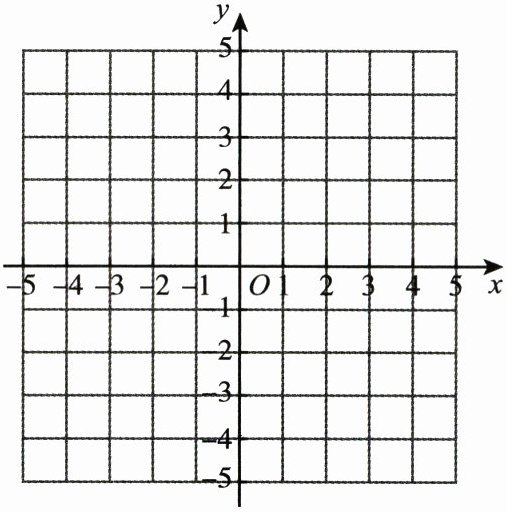
(2)在给定的平面直角坐标系中画出这个二次函数的图象.
(3)当函数值$y < 0$时,对应的$x$的取值范围是.
(4)当$-3 < x < 3$时,直接写出$y$的取值范围.
一个二次函数图象上部分点的横坐标$x$与纵坐标$y$的对应值如下表所示.


(1)求这个二次函数的解析式.
(2)在给定的平面直角坐标系中画出这个二次函数的图象.
(3)当函数值$y < 0$时,对应的$x$的取值范围是.
(4)当$-3 < x < 3$时,直接写出$y$的取值范围.
答案:
(1) 由表格数据可知,二次函数过点 $(-3,0)$, $(1,0)$, $(0,-3)$,
设二次函数解析式为 $y=a(x+3)(x-1)$,
将点 $(0,-3)$ 代入得:$-3=a × 3 × (-1)$,
解得 $a=1$,
所以二次函数解析式为 $y=(x+3)(x-1)=x^2+2x-3$。
(2)
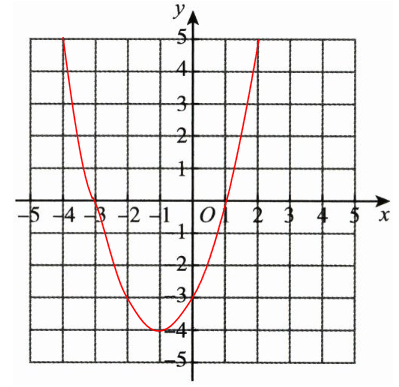
(3) 由表格数据可知,当 $y<0$ 时,$-3<x<1$。
(4) 当 $-3<x<3$ 时,$y$ 的取值范围是 $-4 \leq y<18$。
(1) 由表格数据可知,二次函数过点 $(-3,0)$, $(1,0)$, $(0,-3)$,
设二次函数解析式为 $y=a(x+3)(x-1)$,
将点 $(0,-3)$ 代入得:$-3=a × 3 × (-1)$,
解得 $a=1$,
所以二次函数解析式为 $y=(x+3)(x-1)=x^2+2x-3$。
(2)

(3) 由表格数据可知,当 $y<0$ 时,$-3<x<1$。
(4) 当 $-3<x<3$ 时,$y$ 的取值范围是 $-4 \leq y<18$。
查看更多完整答案,请扫码查看


