24. (本小题满分7分)
如图,正比例函数 y=kx(k≠0)经过点 A(2,4),AB⊥x 轴于点 B.
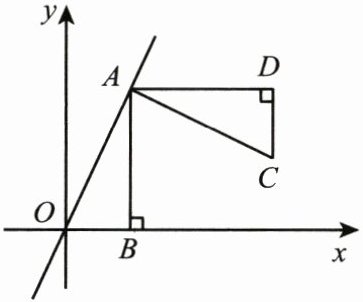
(1)求该正比例函数的解析式.
(2)将△ABO 绕点 A 逆时针旋转 90°得到△ADC,写出点 C 的坐标,试判断点 C 是否在直线$ y=\frac13x+1 $的图象上,并说明理由.
如图,正比例函数 y=kx(k≠0)经过点 A(2,4),AB⊥x 轴于点 B.

(1)求该正比例函数的解析式.
(2)将△ABO 绕点 A 逆时针旋转 90°得到△ADC,写出点 C 的坐标,试判断点 C 是否在直线$ y=\frac13x+1 $的图象上,并说明理由.
答案:
(1) $ y = 2x $;
(2) 点 $ C $ 的坐标为 $ (6,2) $,不在直线 $ y = \frac{1}{3}x + 1 $ 上。
(1) $ y = 2x $;
(2) 点 $ C $ 的坐标为 $ (6,2) $,不在直线 $ y = \frac{1}{3}x + 1 $ 上。
25. (本小题满分8分)
如图①,△ABC 是等腰直角三角形,四边形 ADEF 是正方形,点 D,F 分别在边 AB,AC 上,此时 BD=CF,BD⊥CF 成立. 如图②,当将正方形 ADEF 绕点 A 逆时针旋转角 θ(0°<θ<90°)时,BD=CF 成立吗?请说明理由.
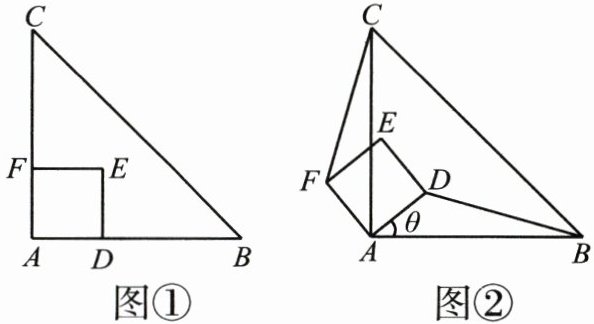
如图①,△ABC 是等腰直角三角形,四边形 ADEF 是正方形,点 D,F 分别在边 AB,AC 上,此时 BD=CF,BD⊥CF 成立. 如图②,当将正方形 ADEF 绕点 A 逆时针旋转角 θ(0°<θ<90°)时,BD=CF 成立吗?请说明理由.

答案:
BD=CF成立。理由如下:
∵△ABC是等腰直角三角形,
∴AB=AC,∠BAC=90°。
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°。
∵∠BAC=∠DAF=90°,
∴∠BAC - ∠DAC=∠DAF - ∠DAC,即∠BAD=∠CAF。
在△ABD和△ACF中,
$\left\{\begin{array}{l} AB=AC \\ ∠BAD=∠CAF \\ AD=AF \end{array}\right.$
∴△ABD≌△ACF(SAS)。
∴BD=CF。
综上,BD=CF成立。
∵△ABC是等腰直角三角形,
∴AB=AC,∠BAC=90°。
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°。
∵∠BAC=∠DAF=90°,
∴∠BAC - ∠DAC=∠DAF - ∠DAC,即∠BAD=∠CAF。
在△ABD和△ACF中,
$\left\{\begin{array}{l} AB=AC \\ ∠BAD=∠CAF \\ AD=AF \end{array}\right.$
∴△ABD≌△ACF(SAS)。
∴BD=CF。
综上,BD=CF成立。
查看更多完整答案,请扫码查看


