26. (本小题满分8分)
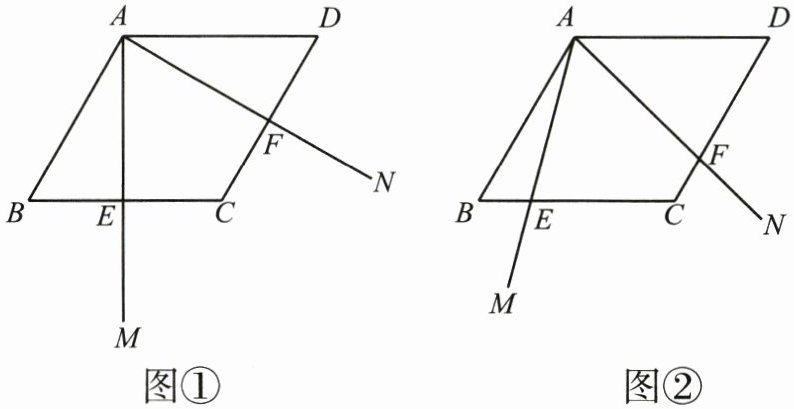
如图,已知菱形 ABCD,∠B=60°,将一个 60°的∠MAN 的顶点与该菱形的顶点 A 重合,以 A 为旋转中心,按顺时针方向旋转这个 60°的∠MAN,使它的两边分别交 CB,DC 于点 E,F.
(1)如图①,当 BE=DF 时,AE 与 AF 的数量关系是.
(2)旋转∠MAN,如图②,当 BE≠DF 时,(1)中的结论是否还成立?若成立,请加以证明;若不成立,请说明理由.
如图,已知菱形 ABCD,∠B=60°,将一个 60°的∠MAN 的顶点与该菱形的顶点 A 重合,以 A 为旋转中心,按顺时针方向旋转这个 60°的∠MAN,使它的两边分别交 CB,DC 于点 E,F.
(1)如图①,当 BE=DF 时,AE 与 AF 的数量关系是.
(2)旋转∠MAN,如图②,当 BE≠DF 时,(1)中的结论是否还成立?若成立,请加以证明;若不成立,请说明理由.

答案:
(1) $AE = AF$。
(2) 成立。
证明:
连接$AC$。
因为四边形$ABCD$是菱形,
所以$AB = AC$,$AD=AB$,
所以$AB = AC=AD$,
又因为$\angle B = 60°$,
所以$\triangle ABC$是等边三角形,
所以$\angle B=\angle ACB = \angle BAC = 60°=\angle ACD$,
又因为$\angle MAN = 60°$,
所以$\angle BAE+\angle EAC=\angle CAF+\angle EAC = 60°$,
所以$\angle BAE=\angle CAF$,
在$\triangle ABE$和$\triangle ACF$中,
$\begin{cases}\angle B=\angle ACF, \\ AB = AC, \\ \angle BAE=\angle CAF.\end{cases}$
所以$\triangle ABE\cong\triangle ACF(ASA)$,
所以$AE = AF$。
(1) $AE = AF$。
(2) 成立。
证明:
连接$AC$。
因为四边形$ABCD$是菱形,
所以$AB = AC$,$AD=AB$,
所以$AB = AC=AD$,
又因为$\angle B = 60°$,
所以$\triangle ABC$是等边三角形,
所以$\angle B=\angle ACB = \angle BAC = 60°=\angle ACD$,
又因为$\angle MAN = 60°$,
所以$\angle BAE+\angle EAC=\angle CAF+\angle EAC = 60°$,
所以$\angle BAE=\angle CAF$,
在$\triangle ABE$和$\triangle ACF$中,
$\begin{cases}\angle B=\angle ACF, \\ AB = AC, \\ \angle BAE=\angle CAF.\end{cases}$
所以$\triangle ABE\cong\triangle ACF(ASA)$,
所以$AE = AF$。
查看更多完整答案,请扫码查看


