《2025年云南省标准教辅优佳学案配套测试卷九年级数学上册人教版》

8. 一个不透明的盒子中有若干个白球，在不允许将球倒出来的情况下，为估计白球的个数，小刚向其中放入8个黑球，摇匀后从中随机摸出一个球记下颜色，再把它放回盒中，不断重复，共摸球400次，其中88次摸到黑球. 估计盒中大约有白球().

A.28个
B.30个
C.36个
D.42个

答案： A

9. 四张完全相同的卡片上，正面分别画有圆、矩形、等边三角形、正五边形四个图案.现把它们的正面向下随机摆放在桌面上，从中任意抽出一张，则抽出的卡片正面图案是中心对称图形的概率为().

A.$\frac{1}{4}$
B.$\frac{1}{2}$
C.$\frac{3}{4}$
D.1

答案： B

10. 一个不透明的箱子内装有53个白球及2个红球，这些球除颜色外无其他差别. 小芬打算从箱子内摸球，以每次摸出一个球后将球再放回的方式摸球53次. 箱子内每个球被摸到的机会相等，且前52次中摸到白球51次及红球1次，则第53次摸球时，小芬摸到红球概率为().

A.$\frac{1}{2}$
B.$\frac{1}{3}$
C.$\frac{2}{53}$
D.$\frac{2}{55}$

答案： D

11. 在数字-1，1，2中任取两个数作为某个点的坐标，那么该点刚好在一次函数$y = x - 2$图象上的概率是().

A.$\frac{1}{2}$
B.$\frac{1}{3}$
C.$\frac{1}{4}$
D.$\frac{1}{6}$

答案： D

12. 一个均匀的立方体的六个面上分别标有数字1，2，3，4，5，6，如图是这个立方体的表面展开图. 抛掷这个立方体，则朝上一面的数恰好等于朝下一面的数的$\frac{1}{2}$的概率是().

A.$\frac{1}{6}$
B.$\frac{1}{3}$
C.$\frac{1}{2}$
D.$\frac{2}{3}$

答案： A

13. 如图，一飞镖游戏板由大小相等的小正方形格子构成，向游戏板随机投掷一枚飞镖，击中阴影区域的概率是().

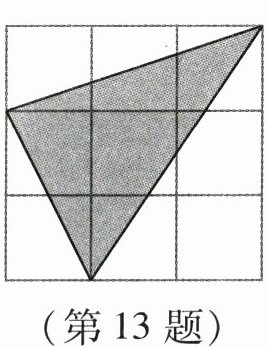
A.$\frac{7}{18}$
B.$\frac{5\sqrt{2}}{9}$
C.$\frac{1}{2}$
D.$\frac{5}{9}$

答案： D

14. 如图，等边三角形内接于大$\odot O$，小$\odot O$是等边三角形的内切圆，随意向大$\odot O$内部区域抛一个小球，则小球落在阴影区域的概率为().

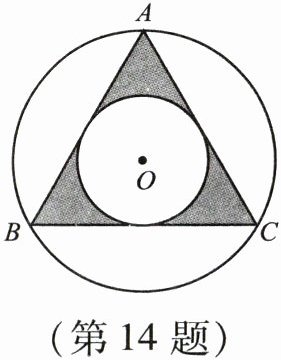
A.$\frac{3\sqrt{3} - \pi}{4\pi}$
B.$\frac{3\sqrt{3}}{8\pi}$
C.$\frac{2\pi - \sqrt{3}}{8\pi}$
D.$\frac{\pi - 1}{4\pi}$

答案： A