《2025年云南省标准教辅优佳学案配套测试卷九年级数学上册人教版》

24. (本小题满分8分)
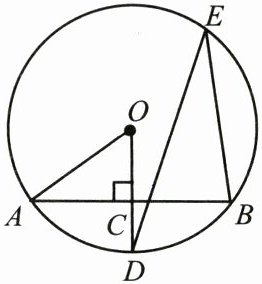
如图，AB是⊙O的一条弦，OD⊥AB，垂足为C，交⊙O于点D，点E在⊙O上.
(1)若∠AOD = 52°，求∠DEB的度数.
(2)若OC = 3，OA = 5，求AB的长.

答案：
(1)
∵ $OD \perp AB$，
∴ $\overset{\frown}{AD} = \overset{\frown}{BD}$，
∴ $\angle DEB = \frac{1}{2} \angle AOD = \frac{1}{2} × 52° = 26°$。
(2)
∵ $OC = 3$, $OA = 5$，
∴ $AC = \sqrt{OA^2 - OC^2} = \sqrt{5^2 - 3^2} = 4$，
∵ $OD \perp AB$，
∴ $AC = BC$，
∴ $AB = 2AC = 8$。

25. (本小题满分8分)
如图，△ABC内接于⊙O，AB是⊙O的直径，C是$\overset{\frown}{AD}$的中点，弦CE⊥AB于点H，连接AD，分别交CE，BC于点P，Q.
(1)求证：P是线段AQ的中点.
(2)若⊙O的半径为5，D是$\overset{\frown}{BC}$的中点，求弦CE的长.

答案：
(2) $5\sqrt{3}$