《2025年云南省标准教辅优佳学案配套测试卷九年级数学上册人教版》

26. (本小题满分8分)
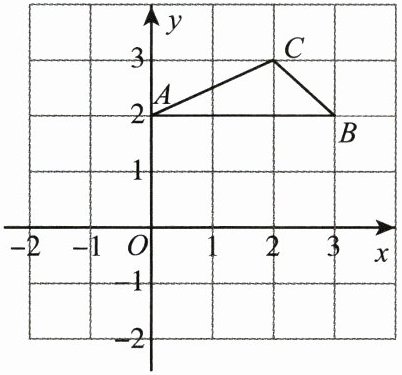
如图，在平面直角坐标系中，点$A$，$B$，$C$的坐标分别为$(0,2)$，$(3,2)$，$(2,3)$.
(1)请在图中画出将$\bigtriangleup ABC$向下平移3个单位长度后所得到的$\bigtriangleup A^{\prime}B^{\prime}C^{\prime}$.
(2)若一个二次函数的图象经过(1)中$\bigtriangleup A^{\prime}B^{\prime}C^{\prime}$的三个顶点，求此二次函数的解析式.

答案：

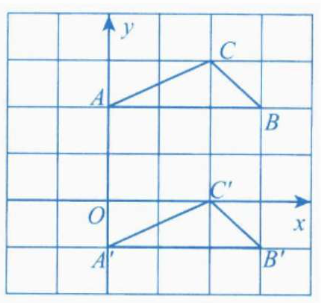
$解：(1)如图所示$

$(2)由图可得A'(0，-1)、B'(3，-1)、C'(2，0)$

$设该二次函数的解析式为y=ax^2+bx+c(a≠0)$

$将点A'、B'、C'代入可得$

$\begin{cases}c=-1\\9a+3b+c=-1\\4a+2b+c=0\end{cases}$

$解得\begin{cases}a=-\dfrac 12\\b=\dfrac 32\\c=-1\end{cases}$

$∴该二次函数的解析式为y=-\frac 12x^2+\frac 32x-1$