《2025年云南省标准教辅优佳学案配套测试卷九年级数学上册人教版》

15. 某中学有一块长$30\ m$、宽$20\ m$的矩形空地，计划在这块空地上划出$\frac{1}{4}$的区域种花，小禹同学的设计方案如图所示，求花带的宽度.设花带的宽度为$x\ m$，则可列方程为().


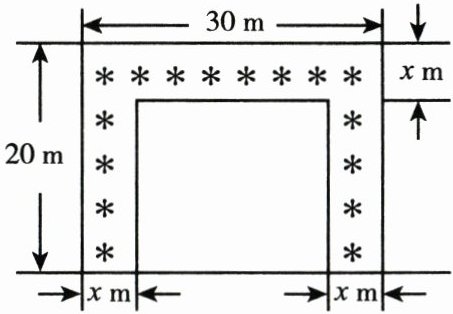
A.$(30 - x)(20 - x) = \frac{3}{4} × 20 × 30$
B.$(30 - 2x)(20 - x) = \frac{1}{4} × 20 × 30$
C.$30x + 2 × 20x = \frac{1}{4} × 20 × 30$
D.$(30 - 2x)(20 - x) = \frac{3}{4} × 20 × 30$

答案： D

16. 若$x = -2$是方程$x^2 + px + 2q = 0$的一个根，则$p - q$的值是.

答案： $2$

17. 下面是一个简单的数值转换程序，则输入的$x$的值为.
输入$x$→$y = (x - 1)^2$→$z = y × (-3)$→输出$z = -9$

答案： $1+\sqrt{3}$或$1 - \sqrt{3}$（填写具体形式或数值框中通常题目给选项这里按题目要求直接填结果形式）因本题为填空题形式给出答案则为具体值形式。

18. 已知代数式$x(x - 5) + 1$与$9x - 6$的值互为相反数，则$x =$.

答案： $1$（或 $-5$）（填写两个解对应的选项（若题目为选择题则根据实际选项选择，若非选择题则直接给出答案数值），此处假设为需要填写数值的非选择题格式，因此直接给出$x$的解，若为选择题则根据具体选项选择标签。）

19. 若一个直角三角形的斜边长为20，一条直角边比另一条直角边长4，则这两条直角边的长度分别为.

答案： 12和16

20. (本小题满分7分)
解下列方程.
(1)(4分)$(x - 2)(x + 3) = 5$；
(2)(3分)$(2x - 1)^2 = 3(2x - 1)$.

答案：
(1)
$(x - 2)(x + 3) = 5$
$x^2 + 3x - 2x - 6 = 5$
$x^2 + x - 11 = 0$
$a=1, b=1, c=-11$
$\Delta = b^2 - 4ac = 1 + 44 = 45$
$x = \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{-1 \pm 3\sqrt{5}}{2}$
$x_1 = \frac{-1 + 3\sqrt{5}}{2}, x_2 = \frac{-1 - 3\sqrt{5}}{2}$
(2)
$(2x - 1)^2 = 3(2x - 1)$
$(2x - 1)^2 - 3(2x - 1) = 0$
$(2x - 1)(2x - 1 - 3) = 0$
$(2x - 1)(2x - 4) = 0$
$2x - 1 = 0$ 或 $2x - 4 = 0$
$x_1 = \frac{1}{2}, x_2 = 2$