《2025年云南省标准教辅优佳学案配套测试卷九年级数学上册人教版》

19. 在平面直角坐标系中，已知点 P(a-1，a+3)在 x 轴上，将点 P 向上平移 2 个单位长度得到点 Q，则点 Q 关于原点对称的点的坐标为.

答案： $(4,-2)$

20. (本小题满分7分)
如图，在平面内将△BEC 绕点 B 逆时针旋转 60°后得到△BAD，且 AB⊥BC 于点 B，连接 DE. 求证：△BDE≌△BCE.

答案： 证明：
1.
∵△BEC绕点B逆时针旋转60°得到△BAD，

∴由旋转性质得：BC=BD（对应边相等），∠CBD=60°（旋转角）。
2.
∵AB⊥BC，
∴∠ABC=90°。
又
∵旋转角为60°，
∴∠ABE=60°（对应点连线夹角等于旋转角），

∴∠EBC=∠ABC-∠ABE=90°-60°=30°。
3.
∵∠CBD=60°，∠EBC=30°，

∴∠DBE=∠CBD-∠EBC=60°-30°=30°，即∠DBE=∠CBE。
4. 在△BDE和△BCE中，
$\left\{\begin{array}{l} BD=BC \\ ∠DBE=∠CBE \\ BE=BE \end{array}\right.$，

∴△BDE≌△BCE（SAS）。

21. (本小题满分6分)
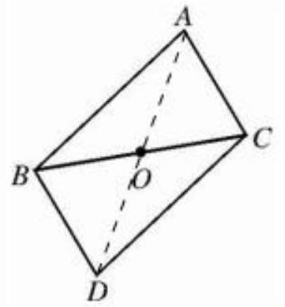
如图，已知△ABC，点 O 为 BC 的中点.

(1)画出将△ABC 绕边 BC 的中点 O 旋转 180°后得到的△DCB.
(2)求证：四边形 ABDC 是平行四边形.

答案：

(1) 

(2) 证明：
∵△ABC 绕点 O 旋转 180°得到△DCB，
∴OA=OD，OB=OC（旋转中心到对应点距离相等）。
∵点 O 为 BC 中点，
∴OB=OC。
∴四边形 ABDC 对角线互相平分，
∴四边形 ABDC 是平行四边形。