《2025年云南省标准教辅优佳学案配套测试卷九年级数学上册人教版》

23. (本小题满分7分)
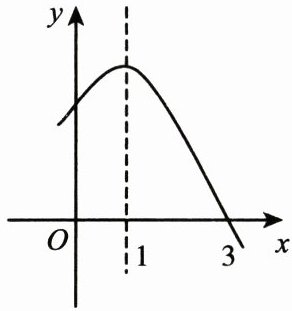
已知二次函数$y = -x^2 + 2x + m$的部分图象如图所示，请你确定关于$x$的一元二次方程$-x^2 + 2x + m = 0$的解.

答案： 由图象可知，二次函数图象的对称轴为$x = 1$，且图象与$x$轴的一个交点为$(3,0)$。
根据对称轴$x = \frac{x_1 + x_2}{2}$（其中$x_1$，$x_2$为方程的两根），设另一交点为$(x_0,0)$，则$\frac{3 + x_0}{2}=1$，解得$x_0=-1$。
所以一元二次方程$-x^2 + 2x + m = 0$的解为$x_1=-1$，$x_2 = 3$。

24. (本小题满分7分)
已知函数$y = (m + 2)x^{m^2 + m - 4}$是关于$x$的二次函数.
(1)求满足条件的$m$的值.
(2)当$m$为何值时，抛物线有最低点？求出此最低点，在此情况下，当$x$为何值时，$y$随$x$的增大而增大？

答案：
(1) 由二次函数定义得：$\begin{cases}m^2 + m - 4 = 2 \\ m + 2 \neq 0\end{cases}$
解方程$m^2 + m - 4 = 2$，即$m^2 + m - 6 = 0$，因式分解得$(m + 3)(m - 2) = 0$，解得$m = -3$或$m = 2$。
又$m + 2 \neq 0$，即$m \neq -2$，所以$m = -3$或$m = 2$。
(2) 抛物线有最低点，则二次项系数大于$0$，即$m + 2 ＞ 0$，解得$m ＞ -2$。
由
(1)知$m = -3$或$m = 2$，所以$m = 2$。
此时函数为$y = 4x^2$，最低点为$(0, 0)$。
当$x ＞ 0$时，$y$随$x$的增大而增大。