《2025年全程助学与学习评估八年级数学上册浙教版》

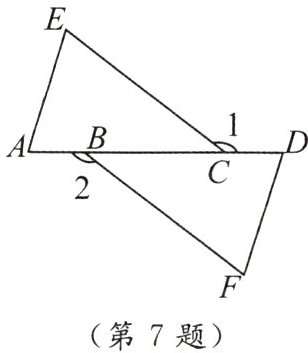
7. 如图,$\triangle ACE≌\triangle DBF$,给出下列结论：①$AC= DB$；②$AB= DC$；③$\angle 1= \angle 2$；④$AE// DF$；⑤$S_{\triangle ACE}= S_{\triangle DFB}$；⑥$BC= AE$；⑦$BF// EC$.其中正确的有(C)

A.$4$个
B.$5$个
C.$6$个
D.$7$个

答案： C

8. 如图,在$\triangle ABC$中,$\angle A:\angle ABC:\angle ACB= 3:5:10$,$B'是AC$延长线上一点,$A'是B'B$延长线上一点,且$\triangle A'B'C≌\triangle ABC$,则$\angle BCA':\angle BCB'= $1:4.

答案： 1:4

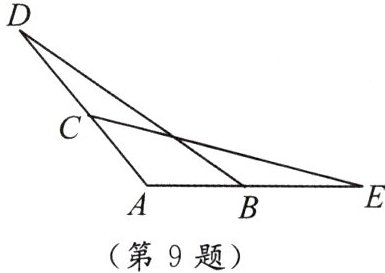
9. 如图,已知$\triangle ABD≌\triangle ACE$,试证明$BE= CD$.

答案： 证明：
∵△ABD≌△ACE，
∴AB=AC，AD=AE（全等三角形对应边相等）。
∵BE=AE-AB，CD=AD-AC，
∴BE=CD。

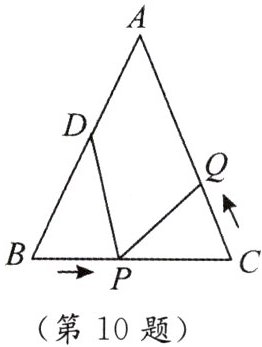
10. 如图,已知在$\triangle ABC$中,$AB= AC= 10\mathrm{cm}$,$BC= 8\mathrm{cm}$,$D为AB$的中点,点$P在线段BC上以3\mathrm{cm}/\mathrm{s}的速度由点B向点C$运动,同时,点$Q在线段CA上由点C向点A以a\mathrm{cm}/\mathrm{s}$的速度运动,设运动的时间为$t\mathrm{s}$.
(1)求$CP$的长(用含$t$的代数式表示).
(2)若以$C$,$P$,$Q为顶点的三角形和以B$,$D$,$P$为顶点的三角形全等,且$\angle B和\angle C$是对应角,求$a$的值.

答案：
(1) 因为点$P$从$B$出发以$3\mathrm{cm/s}$的速度沿$BC$运动，$BC = 8\mathrm{cm}$，所以$BP = 3t\mathrm{cm}$，则$CP=(8 - 3t)\mathrm{cm}$。
(2) 因为$D$为$AB$中点，$AB = 10\mathrm{cm}$，所以$BD=\frac{1}{2}AB = 5\mathrm{cm}$。
分两种情况：
①当$\triangle BPD\cong\triangle CQP$时，$BP = CQ$，$BD = CP$，即$\begin{cases}3t = at\\8 - 3t = 5\end{cases}$，
由$8 - 3t = 5$得$3t = 3$，$t = 1$，把$t = 1$代入$3t = at$得$a = 3$。
②当$\triangle BPD\cong\triangle CQP$（对应点换位）时，$BP = CP$，$BD = CQ$，即$\begin{cases}3t = 8 - 3t\\at = 5\end{cases}$，
由$3t = 8 - 3t$得$6t = 8$，$t=\frac{4}{3}$，把$t = \frac{4}{3}$代入$at = 5$得$a=\frac{15}{4}$。
综上，$a$的值为$3$或$\frac{15}{4}$。