《2025年全程助学与学习评估八年级数学上册浙教版》

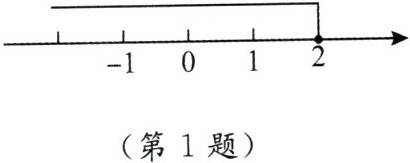
1. 如图,关于 $ x $ 的不等式的解是x＜2.

答案： x＜2

2. 不等式 $ 2 - \frac{x}{2} ＞ 0 $ 的自然数解是0，1，2，3.

答案： $0，1，2，3$

3. 不等式 $ (a - 1)x + 3 ＜ 6 $ 的解为 $ x ＞ -1 $,则 $ a = $-2.

答案： -2

4. 三角形的三条边长为 $ 5 $,$ 1 - 2a $,$ 7 $,则 $ a $ 的取值范围是$-\frac{11}{2} ＜ a ＜ -\frac{1}{2}$.

答案： $-\frac{11}{2} ＜ a ＜ -\frac{1}{2}$

5. 如果 $ a ＜ b ＜ 0 $,那么下列结论中错误的是(C)
A.$ a - 9 ＜ b - 9 $
B.$ -a ＞ -b $
C.$ \frac{1}{b} ＞ \frac{1}{a} $
D.$ \frac{a}{b} ＞ 1 $

答案： C

6. 已知 $ (a - 1)x ＞ a - 1 $ 的解是 $ x ＜ 1 $,则 $ a $ 的取值范围是(B)
A.$ a ＞ 1 $
B.$ a ＜ 1 $
C.$ a ＞ 2 $
D.$ a ＜ 2 $

答案： B

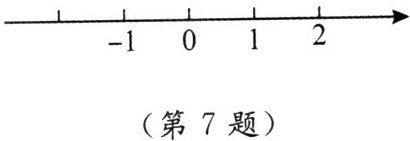
7. 解不等式：$ \frac{x}{3} ＜ 1 - \frac{x + 3}{6} $,并把它的解集在数轴上表示出来.

答案： 1. 去分母，给不等式两边同时乘以6：
$6×\frac{x}{3}＜6×(1 - \frac{x + 3}{6})$
$2x＜6-(x + 3)$
2. 去括号：
$2x＜6 - x - 3$
3. 移项：
$2x+x＜6 - 3$
4. 合并同类项：
$3x＜3$
5. 系数化为1：
$x ＜ 1$
在数轴上表示：画数轴，找到1这个点，用空心圆圈表示（因为不含1），然后向左画一条线表示$x＜1$的范围。

8. 解不等式组：$ \begin{cases} \frac{x - 3}{2} + 3 \geq x, \\ 1 - 3(x - 1) ＜ 8 - x. \end{cases} $

答案： 解不等式组：
$\begin{cases} \frac{x - 3}{2} + 3 \geq x, \\ 1 - 3(x - 1) ＜ 8 - x. \end{cases}$
解不等式①：
$\frac{x - 3}{2} + 3 \geq x$
两边同乘2：
$x - 3 + 6 \geq 2x$
化简：
$x + 3 \geq 2x$
移项：
$3 \geq x \quad 即 \quad x \leq 3$
解不等式②：
$1 - 3(x - 1) ＜ 8 - x$
去括号：
$1 - 3x + 3 ＜ 8 - x$
化简：
$4 - 3x ＜ 8 - x$
移项：
$-3x + x ＜ 8 - 4$
合并同类项：
$-2x ＜ 4$
两边同除以-2（不等号变向）：
$x ＞ -2$
综上，不等式组的解集为：
$-2 ＜ x \leq 3$

9. 求不等式组 $ \begin{cases} 2(x + 1) \leq 14 - 3x, \\ 5x - 2 ＜ 3(x + 2) \end{cases} $ 的非负整数解.

答案： $0, 1, 2$

10. 若 $ |4 - 2m| = 2m - 4 $,那么 $ m $ 的取值范围是(A)
A. $ m \geq 2 $
B. $ m \leq 2 $
C. $ m ＞ 2 $
C. $ m = 2 $

答案： A