6. 如图,在△ABC中,BC>BA,在BC上截取BD= BA,作∠ABC的平分线与AD交于点P,连结PC,若△ABC的面积为$4cm^2,$则△BPC的面积为(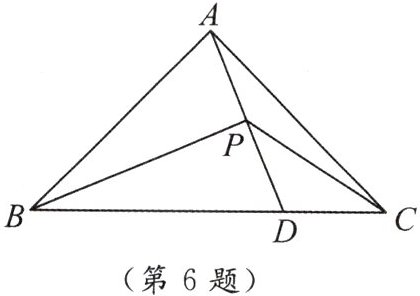
$A.0.5cm^2$
$B.1cm^2$
$C.1.5cm^2$
$D.2cm^2$
D
)
$A.0.5cm^2$
$B.1cm^2$
$C.1.5cm^2$
$D.2cm^2$
答案:
D
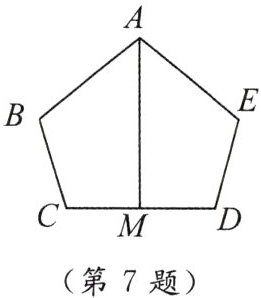
7. 如图,在五边形ABCDE中,∠B= ∠E,AB= AE,BC= DE,M为CD中点. 求证:AM⊥CD.

答案:
证明:连接AC,AD。
在△ABC和△AED中,
∵AB=AE,∠B=∠E,BC=DE,
∴△ABC≌△AED(SAS)。
∴AC=AD。
∴△ACD是等腰三角形。
∵M为CD中点,
∴AM是△ACD底边CD上的中线。
根据等腰三角形三线合一性质,等腰三角形底边上的中线垂直于底边,
∴AM⊥CD。
在△ABC和△AED中,
∵AB=AE,∠B=∠E,BC=DE,
∴△ABC≌△AED(SAS)。
∴AC=AD。
∴△ACD是等腰三角形。
∵M为CD中点,
∴AM是△ACD底边CD上的中线。
根据等腰三角形三线合一性质,等腰三角形底边上的中线垂直于底边,
∴AM⊥CD。
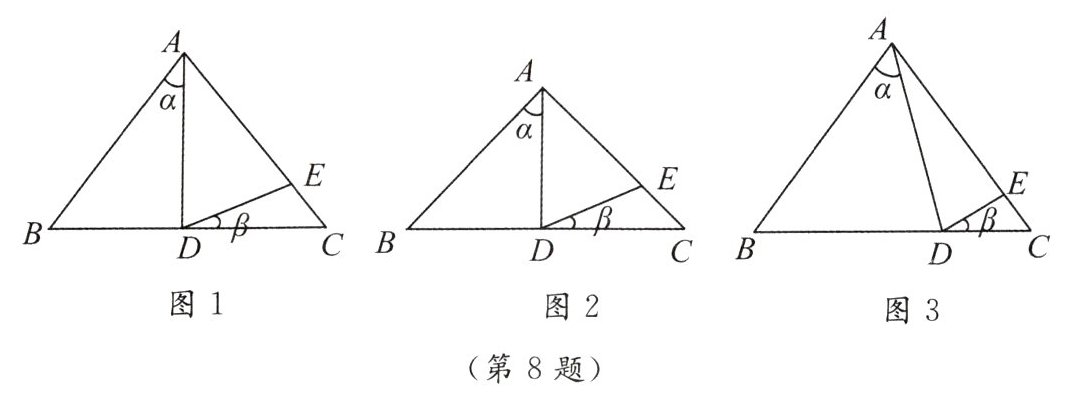
8. 如图,已知在△ABC中,AB= AC,点E为AC边上一点.
(1)如图1,若∠α= 35°,AD是BC上的高,AD= AE,则∠β=
(2)如图2,若∠α= 46°,AD是BC上的高,AD= AE,则∠β=
★(3)如图3,D为BC上任意一点. 请你思考,若AD= AE,则∠α和∠β之间有什么关系?请你写出来,并说明你的理由.
(1)如图1,若∠α= 35°,AD是BC上的高,AD= AE,则∠β=
8.75°
.(2)如图2,若∠α= 46°,AD是BC上的高,AD= AE,则∠β=
11.5°
.★(3)如图3,D为BC上任意一点. 请你思考,若AD= AE,则∠α和∠β之间有什么关系?请你写出来,并说明你的理由.

∠α和∠β之间的关系为α=2β。理由如下:因为AB=AC,所以△ABC是等腰三角形,∠B=∠C。因为AD=AE,所以△ADE是等腰三角形,∠ADE=∠AED。在△ABC中,∠BAC=180°-2∠C。在△ADC中,∠ADC=180°-∠C-∠DAC。又因为∠ADE=∠AED=∠C+∠β(三角形外角性质),且∠ADC=∠ADE+∠β=∠C+∠β+∠β=∠C+2β,所以180°-∠C-∠DAC=∠C+2β,即∠DAC=180°-2∠C-2β。又因为∠BAC=∠BAD+∠DAC,∠BAD=∠α,所以∠α+∠DAC=180°-2∠C,将∠DAC=180°-2∠C-2β代入可得∠α+180°-2∠C-2β=180°-2∠C,化简得α=2β。
答案:
(1)8.75°;
(2)11.5°;
(3)α=2β
(1)8.75°;
(2)11.5°;
(3)α=2β
查看更多完整答案,请扫码查看


