《2025年全程助学与学习评估八年级数学上册浙教版》

7. 定理“等腰三角形的两个底角相等”的逆定理是有两个角相等的三角形是等腰三角形.

答案： 有两个角相等的三角形是等腰三角形

▲8. 我们学习了很多定理,例如：①两直线平行,同位角相等；②全等三角形的对应角相等；③等腰三角形的两个底角相等；④线段垂直平分线上的点到这条线段两个端点的距离相等；⑤角平分线上的点到这个角两边的距离相等. 在上述定理中,存在逆定理的是①③④⑤(填序号).

答案： ①③④⑤

9. 如图,$ \triangle ABC $是等边三角形.
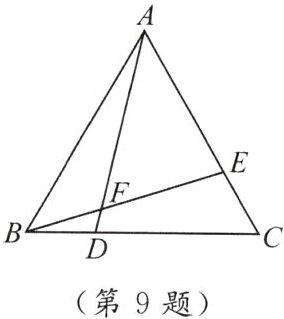
(1) $ D $,$ E $分别为 $ BC $,$ AC $上一点,$ AD $,$ BE $交于 $ F $,且 $ \angle AFE = 60^{\circ} $. 求证：$ AD = BE $.
(2) 第(1)题的逆命题成立吗？若成立,请证明；若不成立,请用反例说明.

答案：
(1) 证明：
∵△ABC是等边三角形，
∴AB=AC，∠BAC=∠ABC=∠C=60°．
∵∠AFE=60°，∠AFE=∠ABF+∠BAD（三角形外角性质），
又∠BAC=∠BAD+∠DAC=60°，
∴∠ABF=∠DAC．
在△ABE和△CAD中，
∠ABE=∠CAD，
AB=AC，
∠BAE=∠C=60°，
∴△ABE≌△CAD（ASA），
∴AD=BE．
(2) 不成立．
反例：取等边△ABC，设AB=1，D为BC上一点，BD=1/3，E为AC上一点，AE=1/3．
由余弦定理可算得AD=BE=√7/3，
但此时AD与BE交点F满足∠AFE≠60°（具体计算略），
故逆命题不成立．

10. 已知命题“$ P $是等边三角形 $ ABC $内的一点,若点 $ P $到三边的距离相等,则 $ PA = PB = PC $”.
(1) 证明这个命题.
★(2) 写出它的逆命题,并判断其逆命题是否成立. 若成立,请给出证明.

答案：
(1) 证明：
∵P是等边△ABC内一点，且P到三边距离相等，
∴P在∠BAC、∠ABC、∠ACB的平分线上（到角两边距离相等的点在角平分线上）。
∵△ABC是等边三角形，
∴三条角平分线与三条垂直平分线重合。
∴P在AB、BC、AC的垂直平分线上，
∴PA=PB，PB=PC（线段垂直平分线上的点到两端点距离相等），
∴PA=PB=PC。
(2) 逆命题：P是等边三角形ABC内的一点，若PA=PB=PC，则点P到三边的距离相等。
成立。
证明：
连接PA、PB、PC，设AB=BC=CA=a，P到AB、BC、AC的距离分别为h₁、h₂、h₃。
∵PA=PB=PC，AB=BC=CA，
∴△PAB≌△PBC≌△PCA（SSS），
∴S△PAB=S△PBC=S△PCA。
∵S△PAB=1/2·AB·h₁=1/2·a·h₁，S△PBC=1/2·BC·h₂=1/2·a·h₂，S△PCA=1/2·AC·h₃=1/2·a·h₃，
∴1/2·a·h₁=1/2·a·h₂=1/2·a·h₃。
∵a≠0，
∴h₁=h₂=h₃，即点P到三边距离相等。